

Ein Baumdiagramm dient dazu, Zufallsversuche übersichtlich darzustellen und um herauszufinden, welche Möglichkeiten und welche Ergebnisse aus den Zufallsversuchen entstehen können.
Zunächst einmal ist es unerheblich, ob das Baumdiagramm von links nach rechts oder von oben nach unten oder umgekehrt aufgezeichnet wird. Es gibt einen Ausgangspunkt, Äste und Knotenpunkte, aus denen das Diagramm gebildet wird.
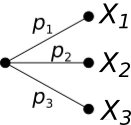
In diesem Baumdiagramm können die Ergebnisse des Zufallsversuch die Zufallsgrößen $X_1$, $X_2$ und $X_3$ sein. Damit ist die Ergebnismenge $\Omega = \{ X_1; X_2; X_3 \}$. An den Ästen, die zu den Ergebnissen führen, stehen die Wahrscheinlichkeiten, mit der das jeweils am Ende des Astes stehende Ergebnis eintritt. Die Äste werden Pfade genannt und zu jedem Ergebnis führt genau ein Pfad. Die Wahrscheinlichkeiten, die an den Pfaden stehen, werden Pfadwahrscheinlichkeiten genannt.
Als Beispiel soll eine Urne dienen, in der Kugeln mit den Zahlen $1$, $2$ und $3$ enthalten sind. Damit sind die Zufallsgrößen $X_1 = 1$, $X_2 = 2$ und $X_3 = 3$. Es sind drei Kugeln mit der $1$, zwei mit der $2$ und vier mit der $3$ in der Urne, insgesamt neun Kugeln. Daraus folgen die Pfadwahrscheinlichkeiten $p_1 = \frac{3}{9}$, $p_2 = \frac29$ und $p_3 = \frac49$.
Jedes Ergebnis hat nun die Wahrscheinlichkeit, die an dem Pfad zu diesem Ergebnis steht. Es gilt also:
\begin{align}
P(1) &= \frac39 \\
P(2) &= \frac 29 \\
P(3) &= \frac 49 \\ \\
\text{allgemein: }P(X_n) &= p_n
\end{align}
Die Aussage ist dann z.B.: Die Wahrscheinlichkeit, eine Kugel mit der $1$ zu ziehen, liegt bei $\frac 39$ oder $0,333$ oder $33,3 \; \%$.
Man kann auch fragen, wie groß die Wahrscheinlichkeit ist, eine ungerade Zahl zu ziehen. Damit wird ein Ereignis $E$ definiert:
$E = \text{ ungerade Zahl}$. Für das Ereignis sind mehrere Ergebnisse möglich, nämlich $1$ oder $3$. Für die gesuchte
Wahrscheinlichkeit des Ereignisses werden die Wahrscheinlichkeiten jedes einzelnen möglichen Ergebnisses addiert (zweite Pfadregel). Es folgt:
\begin{align}
P(E) &= P(1) + P(3) \\
P(E) &= \frac 39 + \frac 49 \\
P(E) &= \frac 79 = 0,778
\end{align}
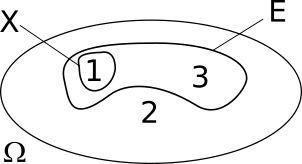
Ein Ergebnis $X$ ist eine Teilmenge der Ereignismenge $E$ und ein Ereignis oder die Ereignismenge $E$ ist eine Teilmenge aller möglichen Ergebnisse $\Omega$:
$$ X \in E \in \Omega$$
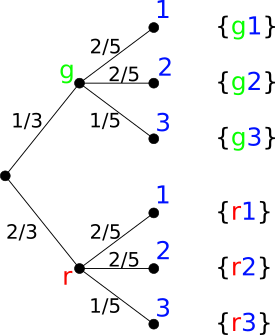
Für die Erläuterungen zu den zweistufigen Zufallsversuchen werden zwei Urnen betrachtet. Die erste Urne enthält drei Kugeln, von denen eine grün ist
und zwei rot. In der zweiten Urne befinden sich fünf Kugeln, von denen jeweils zwei mit der Zahl $1$ bzw. $2$ und eine mit der Zahl $3$
versehen ist.
Die Wahrscheinlichkeit für jedes einzelne Ergebnis lässt sich mit der ersten Pfadregel berechnen. Die erste Pfadregel lautet:
Die Wahrscheinlichkeit am Ende eines Pfades wird berechnet, indem alle Wahrscheinlichkeiten, die entlang des Pfades auftauchen, miteinander
multipliziert werden.
Die einzelnen Ergebnisse sind $\{g1\}$, $\{g2\}$, $\{g3\}$, $\{r1\}$, $\{r2\}$ und $\{r3\}$. Die dazugehörigen Wahrscheinlichkeiten ergeben sich folgendermaßen:
\begin{align}
P(g1) &= \frac 13 \cdot \frac 25 = \frac{2}{15} \\
P(g2) &= \frac 13 \cdot \frac 25 = \frac{2}{15} \\
P(g3) &= \frac 13 \cdot \frac 15 = \frac{1}{15} \\
P(r1) &= \frac 23 \cdot \frac 25 = \frac{4}{15} \\
P(r2) &= \frac 23 \cdot \frac 25 = \frac{4}{15} \\
P(r3) &= \frac 23 \cdot \frac 15 = \frac{2}{15}
\end{align}
Die Wahrscheinlichkeit des Ereignisses $E = \text{ ungerade Zahl}$ ist dann folgende:
\begin{align}
P(E) &= P(g1) + P(g3) + P(r1) + P(r3) \\
P(E) &= \frac{2}{15} + \frac{1}{15} + \frac{4}{15} + \frac{2}{15} \\
P(E) &= \frac{9}{15} = 0,6
\end{align}
Ergebnis $X$: Ein möglicher Ausgang eines Zufallsversuchs
Pfadwahrscheinlichkeit $p$: Die Wahrscheinlichkeit, mit der ein Pfad beschritten wird.
© mondbrand MMXIX