Induktion

Ladungsträger und Magnetfelder

Im Jahre 1820 entdeckte der Däne Hans-Christian Oersted das Gesetz, dass ein elektrischer Strom um sich herum ein Magnetfeld erzeugt. Dieses Magnetfeld besitzt keinen Nord- und Südpol; man bezeichnet es als magnetisches Wirbelfeld. Die Feldlinien des Wirbelfeldes stellt man sich als geschlossene Ringe um den stromdurchflossenen Leiter vor.

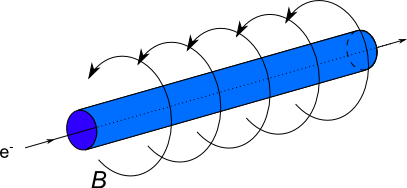
Mit Hilfe des Teilchenmodells der metallischen Leitfähigkeit als Bewegung der Elektronen kann man allgemein sagen, dass sich bewegende Ladungsträger ein Magnetfeld erzeugen. Im Umkehrschluss wirkt sich ein Magnetfeld auf bewegte Ladungsträger aus.

Eine Modellvorstellung liefert das Argument: Die Elektronen im Leiter bewegen sich aus dem Bildschirm heraus und erzeugen so ein Wirbelfeld im Uhrzeigersinn. Ein äußeres Magnetfeld, das nach oben zeigt, überlagert sich im grün markierten Bereich gleichsinnig mit dem Wirbelfeld, d.h. die Magnetfelder zeigen in die gleiche Richtung. Im rot markierten Bereich überlagern sich das äußere und das Wirbelfeld gegensinnig; die Felder zeigen in die entgegengesetzten Richtungen.

Die Feldlinien richten sich aber so ein, dass sie zwischen sich einen konstanten Abstand haben. Damit stoßen sie sich bei der gleichsinnigen Überlagerung ab und ziehen sich bei der gegensinnigen Überlagerung an. Dadurch wird der Leiter in Rchtung der eingezeichneten Kraft $F_L$ gedrückt.
$F_L$ bezeichnet dabei die Lorentz-Kraft, die Kraft, die in einem Magnetfeld auf einen stromdurchflossenen Leiter wirkt.

Ein Leiter, der sich in einem Magnetfeld befindet und von einem Strom durchflossen wird, bewegt sich aufgrund der Lorentzkraft. Die Richtung der Bewegung lässt sich mit der Linke-Hand-Regel herausfinden: Zeigt der Daumen in die Bewegungsrichtung der Elektronen und der Zeigefinger in die Richtung des Magnetfeldes, weist der Mittelfinger in die Richtung der Lorentzkraft.

Induktion nennt man nun den umgekehrten Effekt: Bewegt sich ein Leiter in einem Magnetfeld, erfahren die Ladungen in dem Leiter eine Lorentzkraft, der sie folgen. Daraufhin entsteht auf der einen Seite des Leiters ein Ladungsüberschuss; es entsteht eine Spannung, die sogenannte Induktionsspannung.
Die Richtung der Spannung ist so, dass ein so erzeugter Stromfluss der Ladungsbewegung entgegenwirken würde.

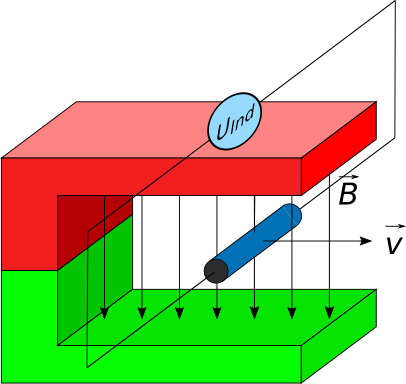
Linkes Bild: Das Magnetfeld wirkt nach unten, die Elektronenbewegung aufgrund des angelegten Stroms zeigt aus der Zeichenebene heraus. Daraufhin entsteht die Lorentzkraft, die den Leiter nach links verschiebt.

Rechtes Bild: Das Magnetfeld wirkt weiterhin nach unten. Betrachtet wird ausschließlich die Bewegung des Leiters mit der Geschwindigkeit $v$, die wegen der Lorentzkraft entstanden ist. Diese Bewegung des gesamten Leiters bedeutet auch, dass sich die Elektronen im Leiter in diese Richtung bewegen. Mit dieser neuen Bewegungsrichtung entsteht eine neue Lorentzkraft, die die Elektronen in die Zeichenebene hinein verschiebt. Damit bewegen sie sich entgegen der ursprünglich angelegten Elektronenbewegungsrichtung und hemmen den Stromfluss.

Entsprechend kann man auch einen Leiter zunächst im Magnetfeld nach links bewegen (rechtes Bild). Daraufhin entsteht die Lorentzkraft, die die Elektronen im Leiter in die Zeichenebene verschiebt. Durch diese neue Bewegung entsteht auch eine neue Lorentzkraft, die den Leiter nach rechts bewegen möchte (linkes Bild), also der ursprünglichen Bewegung entgegen.

Relativbewegung zwischen Ladungen und Magnetfeldlinien

Induktion tritt auf, wenn sich ein Leiterstück innerhalb eines Magnetfeldes bewegt. Die Induktionsspannung entsteht dann zwischen den Enden des Leiterstücks. Für die Größe der Induktionsspannung ist es wichtig, wie lang das Leiterstück ist, das sich im Magnetfeld bewegt. Außerdem ist es wichtig, in welche Richtung sich das Leiterstück im Magnetfeld bewegt. Hier gilt, dass die maximale Induktionsspannung erzeugt werden kann, wenn die Bewegung senkrecht zu den Feldlinien erfolgt.

Die Bewegung des Leiterstücks bedeutet, dass sich die im Leiterstück befindlichen Elektronen (Ladungsträger) bewegen. Auf diese wirkt so die Lorentzkraft $F_L = q \cdot v \cdot B$. Durch die Bewegung der Ladungen wird innerhalb des Leiters ein elektrisches Feld erzeugt. Im elektrischen Feld wirken auf die Ladungen elektrische Feldkräfte: $F_{el} = q \cdot E$. Für die elektrische Feldstärke gilt: $E = \frac{U}{d}$, wobei die Spannung hier als Induktionsspannung $U_{Ind}$ wirkt und die Länge des Leiterstücks im Magnetfeld $l$ als Plattenabstand $d$ im Plattenkondensator eingesetzt wird. Die Annahme ist hierbei, dass das elektrische Feld innerhalb des Leiters einem homogenen elektrischen Feld eines Plattenkondensators entspricht.

Bei einer konstanten Bewegungsgeschwindigkeit des Leiters stellt sich ein Kräftegleichgewicht ein, denn die Lorentzkraft wirkt aufgrund der Bewegung des Leiterstücks im Magnetfeld. Die entstehende Spannung aufgrund der Ladungstrennung wird immer größer, wenn die Bewegung länger anhält. Damit wird auch die Kraftwirkung aufgrund des elektrischen Feldes immer größer, solange bis sie genauso groß ist wie die Lorentzkraft. Es folgt \begin{align} F_L &= F_{el} \\ \\ q \cdot v \cdot B &= q \cdot \frac{U_{Ind}}{l} \\ \\ U_{Ind} &= l \cdot v \cdot B \end{align} Diese Gleichung für die induzierte Spannung eines bewegten Leiters in einem Magnetfeld gilt, wenn die Bewegung und das Magnetfeld senkrecht zueinander stehen.

Beispiel

Ein 50 cm langes, gerades Leiterstück bewegt sich mit $v = 1 \; \frac{\text{m}}{\text{s}}$ senkrecht zum Erdmagnetfeld. In Mitteleuropa hat das Erdmagnetfeld eine magnetische Flussdichte von $B = 44 \; \mu \text{T}$ in der vertikalen Richtung.

In diesem Leiterstück wird also eine Spannung von \begin{align} U_{Ind} &= 0,5 \text{ m} \cdot 1 \; \frac{\text{m}}{\text{s}} \cdot 44 \cdot 10^{-6} \text{ T} \\ \\ U_{Ind} &= 22 \; \mu \text{V} \end{align} induziert.

Bewegt sich eine Leiterschaukel im Magnetfeld wie ein Fadenpendel hin- und her, wird die jeweils aktuell wirkende Geschwindigkeit durch eine Sinusfunktion beschrieben. Damit entsteht auch eine sinusförmige Induktionsspannung, die wie die Bewegung auch die Richtung wechselt, also eine Wechselspannung.

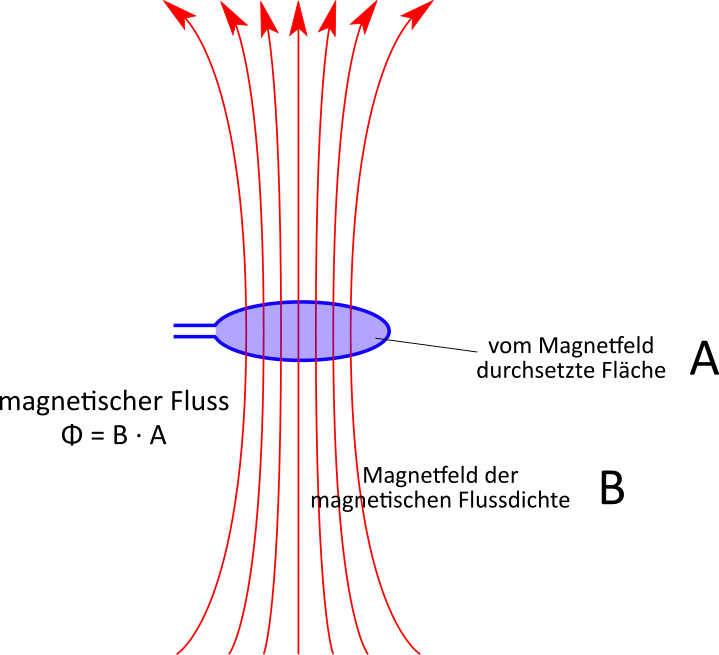Leiterschleife und Magnetfeld - magnetischer Fluss

Wird eine Leiterschleife, also ein zu einem Kreis gebogener Leiter, von einem Magnetfeld durchsetzt, definiert man einen magnetischen Fluss $\Phi$, der dem Produkt von der magnetischen Flussdichte $B$ und der durchsetzten Fläche $A$ entspricht.
Es gilt also $$ \Phi = B \cdot A $$ Dabei ist die Richtung der magnetischen Feldlinien senkrecht zur Fläche. So ist der Fluss maximal. Verlaufen die Feldlinien parallel zur Fläche, ist der Fluss gleich Null.
Damit folgt für eine beliebige Orientierung zwischen Fläche und Feldlinien $$ \Phi = B \cdot A \cdot \cos \alpha $$ mit dem Winkel α zwischen der Feldlinienrichtung und der Senkrechten zur Fläche.

In einer solchen Leiterschleifenanordnung und, wenn die Anzahl der Schleifen größer als Eins ist, einer Spule wird eine Induktionsspannung induziert, wenn sich der magnetische Fluss ändert. Es gilt für eine Spule mit $N$ Windungen: $$ U_{Ind} = - N \cdot \frac{d \Phi}{dt} $$

Der magnetische Fluss ändert sich, wenn sich entweder die durchsetzte Fläche ändert, z.B., wenn sich die Leiterschleife dreht oder wenn sich ein Leiter in ein Magnetfeld hineinschiebt oder herausbewegt, oder wenn sich die magnetische Flussdichte verändert, z.B., wenn ein Magnet in eine Spule hinein- oder herausbewegt wird.
Im allgemeinen Fall kann beides passieren.

Die zeitliche Änderung des Flusses ist die Ableitung von $\Phi$ nach der Zeit.