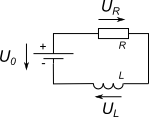
In einem sogenannten RL-Kreis befinden sich neben der Spannungsquelle $U_0$ ein ohmscher Widerstand $R$, über den die Spannung $U_R$ abfällt,
und eine Spule mit der Induktivität $L$, über die die Spannung $U_L$ abfällt.
Führt man einen Maschenumlauf gemäß der zweiten Regel von Kirchhoff durch, entsteht die folgende Gleichung: \begin{align} U_R + U_L - U_0 = 0 \\ \\ U_0 = U_R + U_L \end{align} Jetzt können die Spannungen, die über den Bauteilen abfallen, durch die Ausdrücke für die Stromstärke ersetzt werden: \begin{align} U_0 = I \cdot R + L \cdot \frac{dI}{dt} \end{align} Umgestellt nach $\frac{dI}{dt}$ folgt \begin{align} \frac{dI}{dt} = \frac{U_0}{L} - \frac{R}{L} \cdot I \end{align} Hier handelt es sich um eine inhomogene Differentialgleichung erster Ordnung, deren Lösung die Funktion für die zeitabhängige Stromstärke im RL-Kreis darstellt: \begin{align} I(t) = I_0 \left( 1 - e^{- \frac{R}{L} t} \right) \end{align} Lösung der Differentialgleichung bedeutet, dass die Funktion die Differentialgleichung erfüllt, wenn man sie und ihre Ableitung in die Dgl. einsetzt. Für die Überlegungen zum RL-Kreis ist zunächst noch die Ableitung von $I(t)$ wichtig: \begin{align} \frac{dI(t)}{dt} = \frac{I_0 \cdot R}{L} \cdot e^{- \frac{R}{L} t} \end{align} Der Term $I_0 \cdot R$ wird durch $U_0$ ersetzt: \begin{align} \frac{dI(t)}{dt} = \frac{U_0}{L} \cdot e^{- \frac{R}{L} t} \end{align} Für die Spannung, die über der Spule abfällt, erhält man so \begin{align} U_L &= L \cdot \frac{dI}{dt} \\ \\ U_L &= U_0 \cdot e^{- \frac{R}{L} t} \end{align} Durch den Stromkreis fließt der Strom $I(t)$. Damit fällt über den ohmschen Widerstand die Spannung $U_R = I(t) \cdot R$ ab. Mit der Lösungsfunktion $I(t)$ erhält man für die Spannung \begin{align} U_R &= R \cdot I_0 \cdot \left( 1 - e^{- \frac{R}{L} t} \right) \\ \\ U_R &= U_0 \cdot \left( 1 - e^{- \frac{R}{L} t} \right) \end{align} Sieht man sich die beiden Spannungen $U_R$ und $U_L$ an, kann man erkennen, dass niemals beide Spannungen gleichzeitig maximal sind. Vielmehr addieren sie sich zu der Spannung $U_0$, der Speisespannung des Stromkreises.
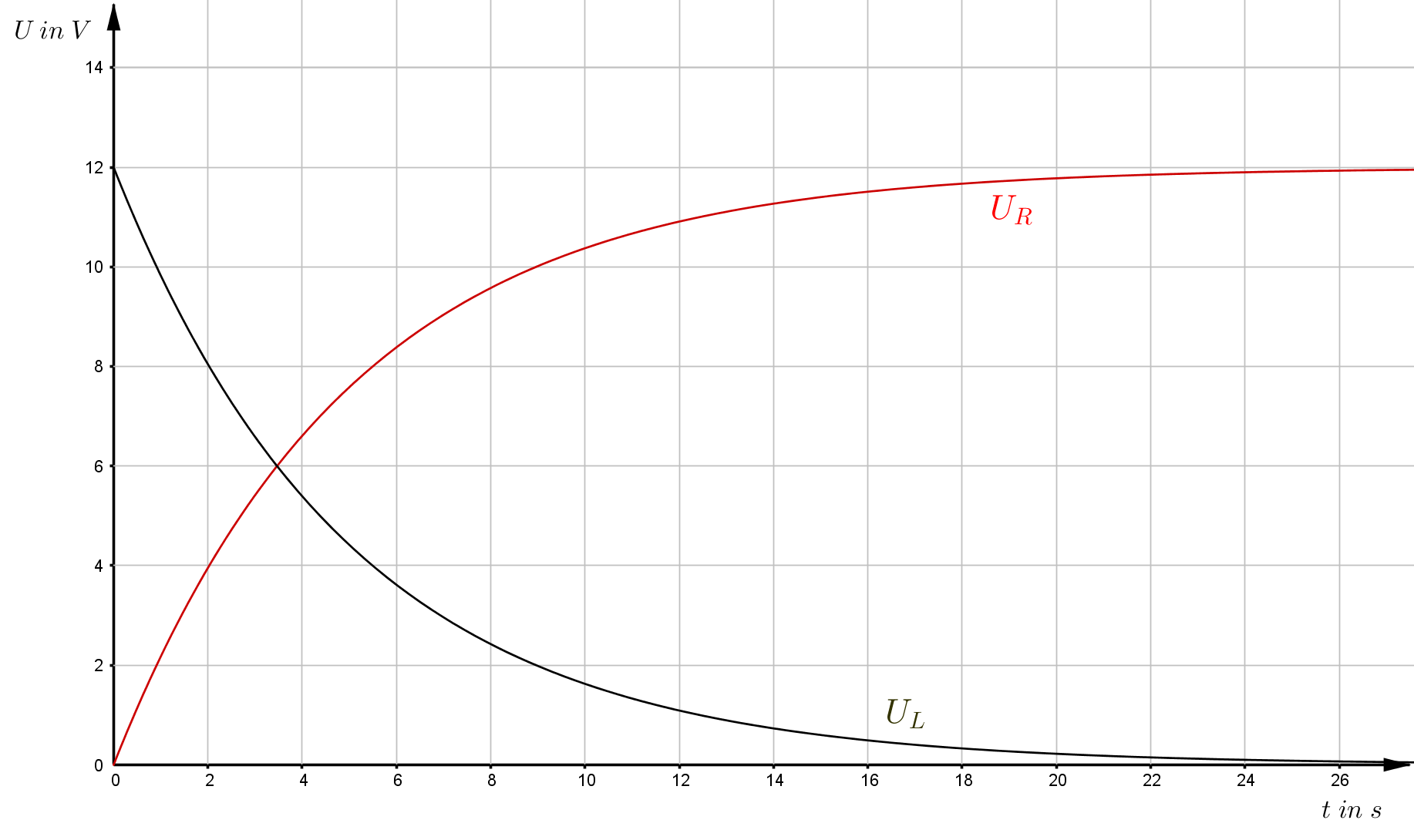
Auch der Verlauf der Stromstärke zeigt, dass zu Beginn kein Strom fließt. Die Stromstärke steigt zunächst stark an, dann weniger, bis sie schließlich die maximale Stromstärke $I_0$ erreicht.
In den Beispielverläufen in den Grafiken wurden folgende Werte eingesetzt: \begin{align} U_0 &= 12 \text{ V} \\ R &= 100 \, \Omega \\ L &= 500 \text{ H} \end{align}
Der Term $\frac{L}{R}$, der als Kehrwert im Exponenten der $e$-Funktion vorkommt, wird auch Zeitkonstante $\tau$ genannt. Also $$ \tau = \frac{L}{R} $$ Die Größe ist ein Maß dafür, wie schnell der Einschaltvorgang abgeschlossen ist. Je kleiner $\tau$, desto schneller wird $I_0$ erreicht. Dabei gilt, dass zum Erreichen des Gleichgewichtszustands etwa $5 \tau$ vergehen, im Beispiel also 25 s.
Zu Beginn, wenn der Strom anfängt zu fließen, ist die Änderung der Stromstärke an größten. Dadurch wird in der Spule die größte Spannung
induziert, die zum Zeitpunkt $t = 0$ nahezu gleich der Speisespannung ist. Die in der Spule induzierte Spannung erzeugt einen Strom, der dem
äußeren Strom entgegengesetzt ist. Insgesamt fließt damit fast kein Strom durch den Stromkreis und über dem Widerstand fällt keine Spannung ab.
Die Stromstärke steigt also nur langsam an, da sie durch die Spule behindert wird. Die Behinderung durch die Spule wird nach und nach immer
schwächer, da die Änderung der Stromstärke kleiner wird. Schließlich wird die Spannung über der Spule Null und die gesamte Spannung fällt
über dem Widerstand ab. Die Stromstärke ist jetzt maximal.
© mondbrand MMXIX