Wenn eine Funktion untersucht werden muss, werden im Grunde immer dieselben Werkzeuge benötigt. Je nach der Art der Funktion werden bestimmte Untersuchungsschritte mehr oder weniger benötigt. Aber grundsätzlich gelten die Schritte für alle Funktionen.
Allerdings ist es so, dass es in den wenigsten Fällen tatsächlich notwendig ist, immer alles zu untersuchen. Je nach Anwendungsgebiet und Fragestellung werden nur bestimmte Werkzeuge gebraucht und andere gar nicht.
Damit gilt, dass die Fragestellung definiert, was gemacht werden muss. Die typische komplette „Kurvendiskussion“ ist hingegen nicht üblich.
Was also kann untersucht werden?
Ganzrationale Funktionen
Bei ganzrationalen Funktionen ist der Definitionsbereich prinzipiell gleich der Menge der reellen Zahlen: $$ D \in \mathbb{R} $$ Einschränkung: Dies gilt nur, wenn der Exponent der Potenzen ganzzahlig ist.
Gebrochen-rationale Funktionen
Der Definitionsbereich ist bei gebrochenrationalen Funktionen ein wichtiger Punkt, denn wenn die Funktion in einen Zähler und einen Nenner unterteilt werden kann, kann der Nenner auch Null werden, wenn der „richtige“ $x$-Wert eingesetzt wird.
Für Funktionen der Form $$ f(x) = \frac{Z(x)}{N(x)} $$ wird untersucht, für welche $x$ gilt: $N(x) = 0$.
Die $x$-Werte, bei denen der Nenner Null wird, sind aus dem Definitionsbereich ausgeschlossen.
Beispiel:
Es sei $f(x) = \frac{3 x^2}{2 x^3 - x}$. Hier ist $Z(x)= 3x^2$ und $N(x)=2 x^3 - x$.
Also folgt:
\begin{align}
N(x) &= 0 \\
2 x^3 - x & = 0 \\
x (2 x^2 - 1) & = 0 \\ \\
x = 0 \wedge 2 x^2 & - 1 = 0 \\
x^2 - \frac{1}{2} & = 0 \\
x^2 & = \frac{1}{2} \\
x & = \pm 0,707
\end{align}
Es gibt also drei $x$-Werte, bei denen der Nenner Null wird: $x_1 = - 0,707$, $x_2 = 0$ und $x_3 = 0,707$.
Für den Definitionsbereich folgt damit:
$$
D \in \mathbb{R} \backslash \{ -0,707; 0; 0,707 \}
$$
Zu lesen: Der Definitionsbereich umfasst die Menge der reellen Zahlen ohne -0,707, 0 und 0,707.
Der Graph der Funktion sieht dann so aus:
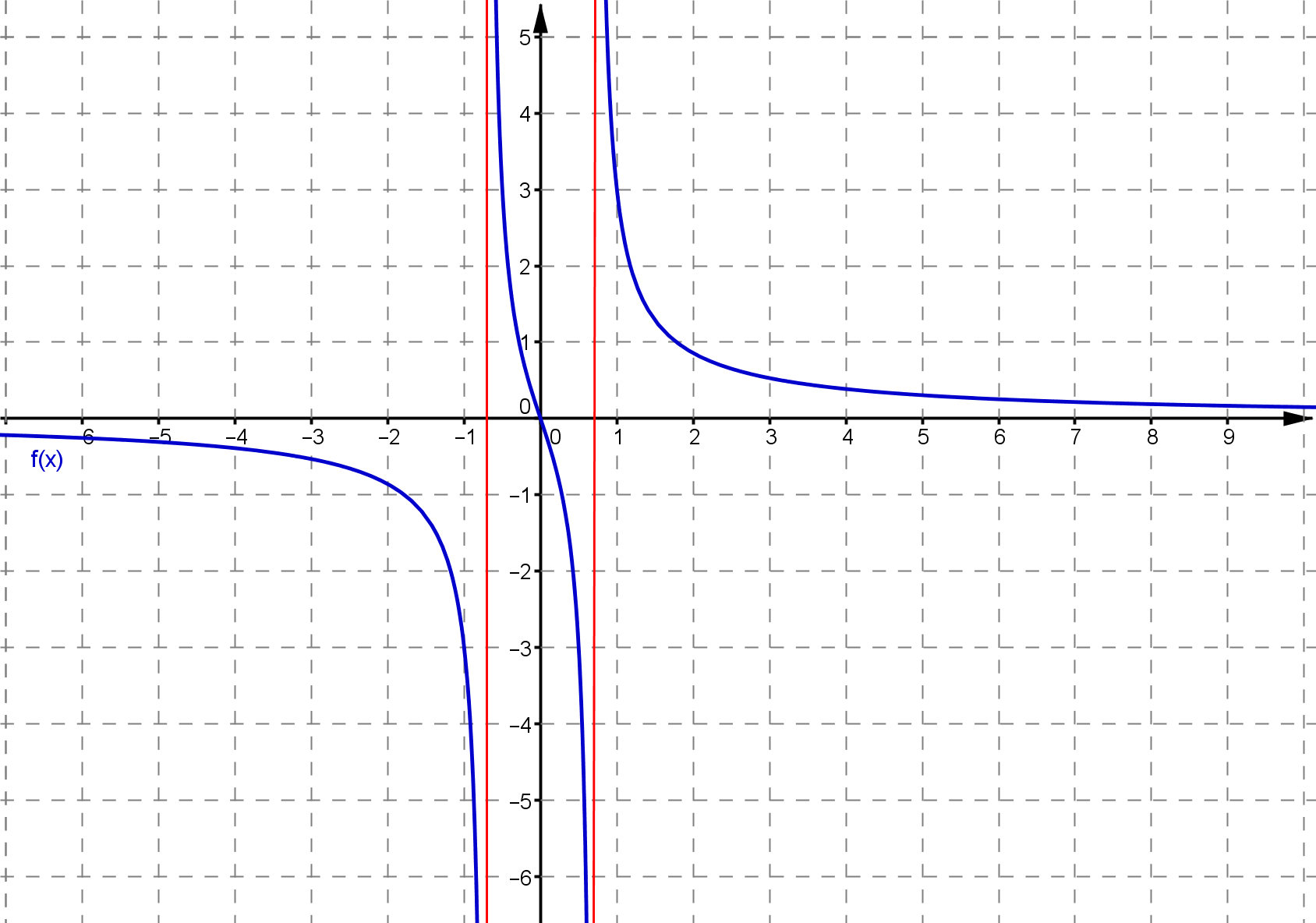
In blau ist der Graph der Funktion $f(x)$ zu sehen. Rot eingezeichnet sind die beiden $x$-Werte -0,707 und 0,707. Nicht zu sehen ist der dritte Wert $x=0$. Der Funktionsgraph hat an dieser Stelle eine Lücke, d.h. einen Punkt, der nicht definiert ist.
Das Verhalten des Graphen bei Annäherung an die„verbotenen“ $x$-Werte wird später noch von Interesse sein. Zunächst reicht es zu erkennen, dass sich der Graph an die betreffenden $x$-Werte annähert.
Trigonometrische Funktionen
Der Definitionsbereich trigonometrischer Funktionen ist prinzipiell gleich der Menge der reellen Zahlen: $$ D \in \mathbb{R} $$ Dies gilt für $f(x) = \sin(x)$ und $f(x) = \cos(x)$. Eine Ausnahme bilden die
Tangensfunktionen
$$
f(x)= \tan (x)
$$
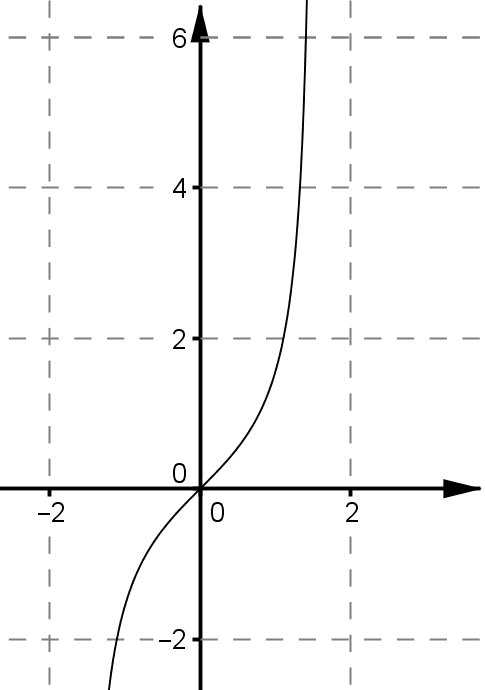Für diese gilt, dass sie von $- \frac{\pi}{2}$ bis $ \frac{\pi}{2}$ definiert ist. Die Werte $- \frac{\pi}{2}$ und $ \frac{\pi}{2}$
gehören aber nicht dazu. Also:
$$
D= \{ x \mid - \frac{\pi}{2} < x < \frac{\pi}{2} \}
$$
Zu lesen: Der Definitionsbereich ist die Menge aller $x$, die größer sind als $- \frac{\pi}{2}$ und kleiner sind als $\frac{\pi}{2}$.
Exponentialfunktionen
Funktionen in der Form $f(x) = a^x$ sind prinzipiell für alle $x$-Werte definiert. Also ist der Definitionsbereich $$ D \in \mathbb{R} $$
Wurzelfunktionen
Funktionen der Form $f(x) = \sqrt{x}$ sind beschränkt. Es gilt generell, dass der Term unter der Wurzel größer oder gleich Null sein muss, damit die Funktion definiert ist.
Beispiel:
Es sei $f(x) = \sqrt{2 x^2 - x - 1}$. Untersucht wird nun der Term unter der Wurzel: \begin{align} 2 x^2 - x - 1 &= 0 \\ x^2 - \frac12 x - \frac12 &= 0 \\ \\ x_{1,2} &= \frac14 \pm \sqrt{ \left( \frac14 \right)^2 + \frac12 } \\ x_{1,2} &= \frac14 \pm \sqrt{ \frac{1}{16} + \frac{8}{16} } \\ x_{1,2} &= \frac14 \pm \frac34 \\ x_1 = - \frac12 &\wedge x_2 = 1 \end{align} Der Term hat somit die Nullstellen $x_{N1} = - \frac12$ und $x_{N2} = 1$. Da es sich um einen quadratischen Term handelt, bedeutet dies, dass die Parabel, also der Graph des Terms, zwischen den beiden Nullstellen entweder positiv ist, d.h., oberhalb der $x$-Achse verläuft, oder dass sie negativ ist und unterhalb der $x$-Achse verläuft. Dafür genügt es, einen $x$-Wert in den Tem einzusetzen, z.B. $x = 0$. Für $x = 0$ hat der Term den Wert $-1$, ist also negativ.
Für alle $x$-Werte, die kleiner sind als $- \frac12$ und für alle $x$-Werte, die größer sind als $1$ ist der Term unter der
Wurzel positiv. Für alle $x$-Werte, die größer sind als $- \frac12$ und kleiner sind als $1$ ist der Term negativ. Die Funktion
ist dort nicht definiert. Die $x$-Werte, bei denen der Term gleich Null ist, gehören zum Definitionsbereich. Es folgt insgesamt für den
Definitionsbereich:
$$
D= \{ x \mid x \leqslant - \frac{1}{2} \vee x \geqslant 1 \}
$$
Der Definitionsbereich umfasst die Menge aller $x$, die kleinergleich $- \frac12$ oder größergleich $1$ sind.
Alternativ könnte man den Definitionsbereich auch so beschreiben: $$ D \in \mathbb{R} \backslash \{ - \frac12 < x < 1 \} $$ Der Definitionsbereich umfasst die Menge der reellen Zahlen ohne den Bereich zwischen $- \frac12$ und $1$.
Nullstellen sind die $x$-Werte, bei denen der Funktionswert Null wird, also die Schnittpunkte mit der $x$-Achse. Es gilt: $$ f(x)=0 $$ Mehr: ➜ Bestimmung von Nullstellen
Für gebrochen-rationale Funktionen gilt: $Z(x)=0$
Der $y$-Achsenabschnitt ist der Schnittpunkt der Funktion mit der $y$-Achse. Für diese gilt: \begin{align} x&=0 \\ f(0)&= y_{\text{Ab}} \end{align}
Ein Funktionsgraph kann symmetrisch bezüglich der $y$-Achse oder bezüglich des Koordinatenursprungs sein. Demzufolge unterscheidet man
zwischen Achsensymmetrie (AS) und Punktsymmetrie (PS).
Achsensymmetrische Graphen haben bei $x$ und bei $-x$ die gleichen Funktionswerte.
Die Vorschrift für die Achsensymmetrie lautet: $$ f(x)=f(-x) $$
Beispiel:
Es sei $f(x)=x^2$.
Es gilt: $$f(-x)=(-x)^2=x^2=f(x)$$
Also ist $f(x)=x^2$ achsensymmetrisch.
Für die Punktsymmetrie muss gelten:
$$
f(x)=-f(-x)
$$
Beispiel:
Es sei $f(x)=x^3$.
Es gilt: $$-f(-x)=-(-x)^3=-(-x^3)=x^3=f(x)$$
Also ist $f(x)=x^3$ punktsymmetrisch.
Die Achsensymmetrie bezüglich einer beliebigen senkrechten Achse und die Punktsymmetrie bezüglich eines beliebigen Punktes werden ➜ hier behandelt.
Ganzrationale Funktionen
Für das Verhalten der Funktion $f(x)$ wenn $x \rightarrow \pm \infty$ geht, gibt es verschiedene Möglichkeiten.
Für ganzrationale Funktionen wird dazu nur der Teil mit dem höchsten Exponenten betrachtet. Die Funktion hat dann die Form
$f(x) = a_n \cdot x^n$, wobei $a_n$ der Koeffizient des Terms mit dem höchsten Exponenten darstellt, also beispielsweise
$f(x) = a_3 \cdot x^3 + a_2 \cdot x^2 + a_1 \cdot x + a_0 \qquad \rightarrow \qquad f(x) = a_3 \cdot x^3$.
Das Globalverhalten lässt sich übersichtlich in einer Tabelle darstellen:
| $n$ geradzahlig | $n$ ungeradzahlig | |
| $a_n > 0$ | $f(x) \rightarrow \infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow \infty \text{ für } x \rightarrow \infty$ | $f(x) \rightarrow -\infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow \infty \text{ für } x \rightarrow \infty$ |
| $a_n < 0$ | $f(x) \rightarrow -\infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow -\infty \text{ für } x \rightarrow \infty$ | $f(x) \rightarrow \infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow -\infty \text{ für } x \rightarrow \infty$ |
Gebrochen-rationale Funktionen
Handelt es sich um eine gebrochen-rationale Funktion, wird die Zählerfunktion $Z(x)$ durch die Nennerfunktion $N(x)$
geteilt (Polynomdivision). Der Term, der aus der echten Division entsteht, bildet ab, wie sich die Funktion für $x \rightarrow \infty$ verhält.
Eine echte Division findet statt, wenn der Zählergrad größer als der Nennergrad ist.
Beispiel:
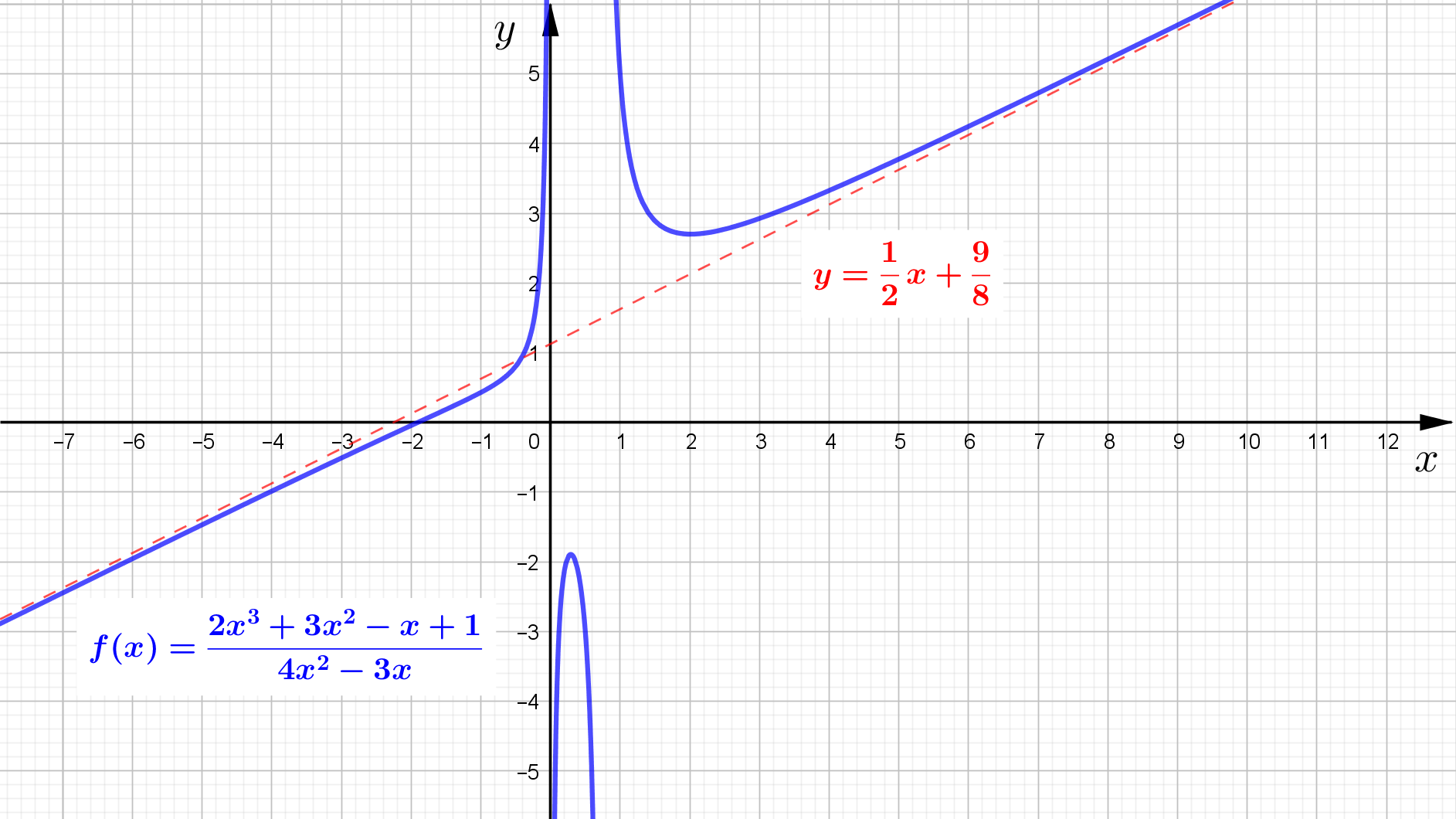$$
f(x)= \frac{2 x^3 + 3 x^2 - x +1}{4 x^2 -3 x}
$$
\begin{align}
\left(2 x^3 + 3 x^2 - x+1 \right) : \left( 4x^2 -3x \right) = \frac{1}{2} x + \frac{9}{8} + \frac{\frac{19}{8} x +1}{4 x^2-3 x} \\
- \underline{\left( 2 x^3 - \frac{3}{2} x^2 \right)} \qquad \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\\
\frac{9}{2} x^2 - x+1 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\,\\
- \underline{\left( \frac{9}{2} x^2 - \frac{27}{8} x \right)} \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\
\frac{19}{8} x +1 \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad
\end{align}
Das Ergebnis $\frac{1}{2} x + \frac{9}{8}$ ist eine Funktion, an die sich die Funktion $f(x)$ anschmiegt. Man nennt sie
Asymptote $\left( y_{Asy}\right)$. Hier also:
$$
y_{Asy}= \frac{1}{2} x + \frac{9}{8}
$$
Der restliche Term des Ergebnisses $\left( R(x) = \frac{\frac{19}{8} x +1}{4 x^2-3 x} \right)$ ist der Abstand der Funktion zu der
Asymptote, der mit zunehmendem $\vert x \vert$ immer kleiner wird. Die Funktion $R(x)$ ist die Differenz der eigentlichen Funktion
$f(x)$ und der Asymptotenfunktion $y_{Asy}$: $\qquad R(x) = f(x) - y_{Asy}$
Beispielsweise betragen die Funktionswerte des Rests der Polynomdivision an den Stellen $x = -4$ und $x = -5$ $R(-4) =-0,112$ und $R(-5) = -0,095$. Die Differenz ist also negativ, was heißt, dass die Funktion $f(x)$ von unten an die Asymptote heranführt. Bei $x = 4$ und $x = 5$ beträgt der Wert des Rests $R(4) = 0,202$ und $R(5) = 0,151$, was bedeutet, dass $f(x)$ von oben an die Asymptote heranführt.
Exponentialfunktionen
Exponentialfunktionen $\left( f(x) = a^x \right)$ haben für unendlich große $x$-Werte ein typisches Verhalten, was allerdings von der Basis $a$ anhängt. Hier kann das Verhalten wieder durch eine Tabelle dargestellt werden:
| $0 < a < 1$ | $a > 1$ | |
| $x \rightarrow \infty$ | $f(x) \rightarrow 0$ | $f(x) \rightarrow \infty$ |
| $x \rightarrow -\infty$ | $f(x) \rightarrow \infty$ | $f(x) \rightarrow 0$ |
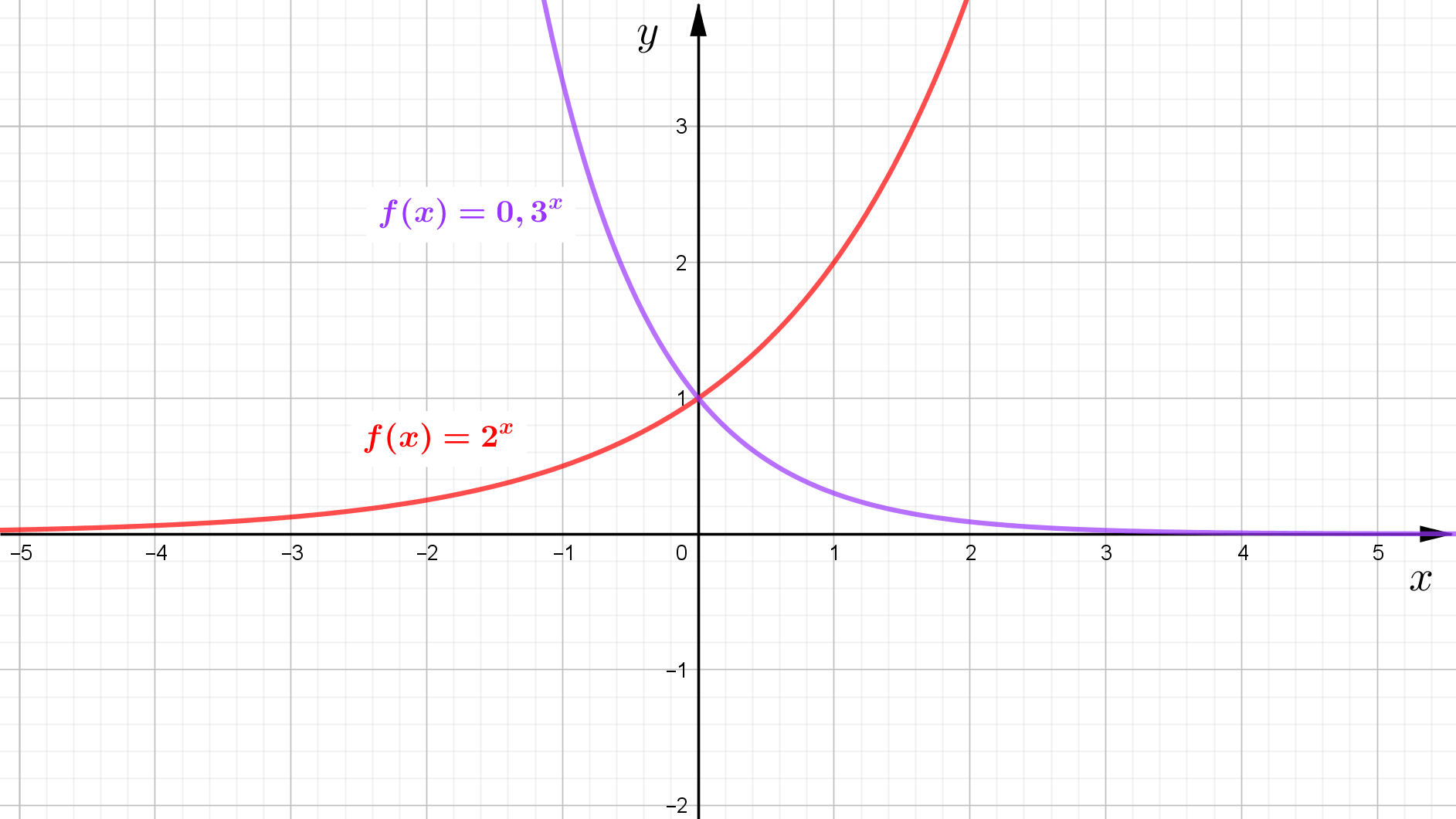
Die Exponentialfunktion $f(x)=2^x$ kommt für $x \rightarrow -\infty$ von der $x$-Achse und steigt für $x \rightarrow \infty$ gegen
Unendlich an.
Die Funktion $f(x) = 0,3^x$ kommt für $x \rightarrow -\infty$ von Unendlich und nähert sich für $x \rightarrow \infty$
an die $x$-Achse an.
Für negative Werte für $a$ ist die Exponentialfunktion nicht definiert.
Die Extremstellen einer Funktion $f(x)$ sind die Nullstellen der Ableitungsfunktion $f'(x)$. Daher muss gelten:
$$
f'(x)=0
$$
Desweiteren muss gelten, dass die Ableitungsfunktion einen Vorzeichenwechsel aufweist. Also:
$$
f''(x) \gtrless 0
$$
Erläuterung zur zweiten Bedingung:
Die zweite Ableitung ist die Steigung der ersten Ableitung. Wenn die erste Ableitung nun einen Vorzeichenwechsel (VZW)
hat, ist die Steigung, also die zweite Ableitung, entweder positiv (= VZW von Minus nach Plus) oder
negativ (= VZW von Plus nach Minus). Wenn die zweite Ableitung positiv ist (VZW Minus $\rightarrow$ Plus), ändert sich
die Steigung der Funktion von negativ nach positiv. Man hat also einen Tiefpunkt / ein Minimum. Ist die zweite Ableitung
negativ, ändert sich die Steigung der Funktion von positiv nach negativ. Es liegt dann ein Hochpunkt / ein Maximum vor.
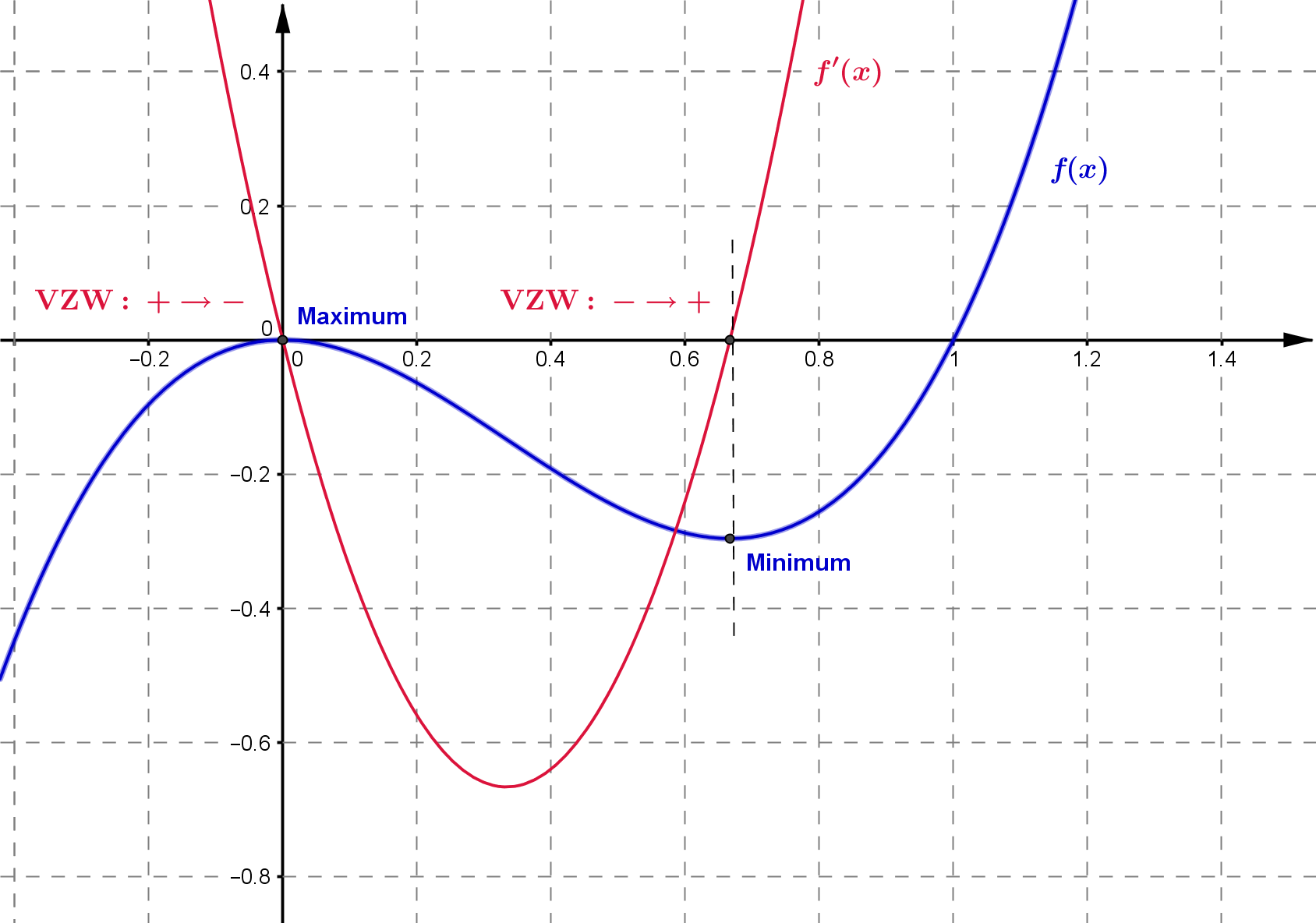
Für Extremstellen gilt also: \begin{align} f'(x)&=0 \\ f''(x) > 0 \; (\text{Minimum}) &\vee f''(x) < 0 \; (\text{Maximum}) \end{align}
Liegen dann die Extremstellen $x_E$ vor, werden sie in die Funktion eingesetzt um die Funktionswerte zu erhalten. Also: $$ f(x_E) $$ Man erhält am Ende die Koordinaten der Extrempunkte: $$ P_E \left( x_E \mid f(x_E) \right) $$
Für Wendepunkte muss gelten: \begin{align} f''(x)&=0\\ f'''(x) & \neq 0 \end{align} Die erhaltenen Wendestellen $x_W$ werden in die Funktion eingesetzt: $f(x_W)$ und man erhält die Wendepunkte: $$ P_W \left( x_W \mid f(x_W) \right) $$
Besitzt die Funktion an der Wendestelle die Steigung Null, sie verläuft also waagerecht an dieser Stelle, bedeutet das, dass ein sogenannter Sattelpunkt vorliegt. Das ist der Fall, wenn $f'(x)$ bei der Extremstelle keinen Vorzeichenwechsel hat. Dann gilt dort: $f'(x) = 0$ und $f''(x) = 0$. Der Sattelpunkt ist (nur) ein besonderer Wendepunkt.
Ist die Funktion neben der freien Variablen $x$ auch noch von einem weiteren Parameter abhängig, spricht man von Funktionsscharen. Diese Scharen weisen natürlich auch alle typischen Punkte auf wie die "normalen" Funktionen. Allerdings hängen die Koordinaten der Nullstellen, Extrempunkte und Wendepunkte meist auch noch von dem zusätzlichen Parameter ab.
Dabei liegen z.B. die Extrempunkte aller Funktionen der Schar auch auf einer speziellen Funktion, der Ortskurve. Um diese zu ermitteln, werden die Abhängigkeiten der Koordinaten vom Parameter benötigt. Für die Ortskurve der Extrempunkte folgt: $$ P_E = \left( x_E \mid f(x_E) \right) $$ Die $x$-Koordinate wird nach dem Parameter umgeformt. Diese Gleichung für den Parameter wird in die $y$-Koordinate eingesetzt. Man erhält eine Funktionsgleichung $y=f(x)$.
Beispiel:
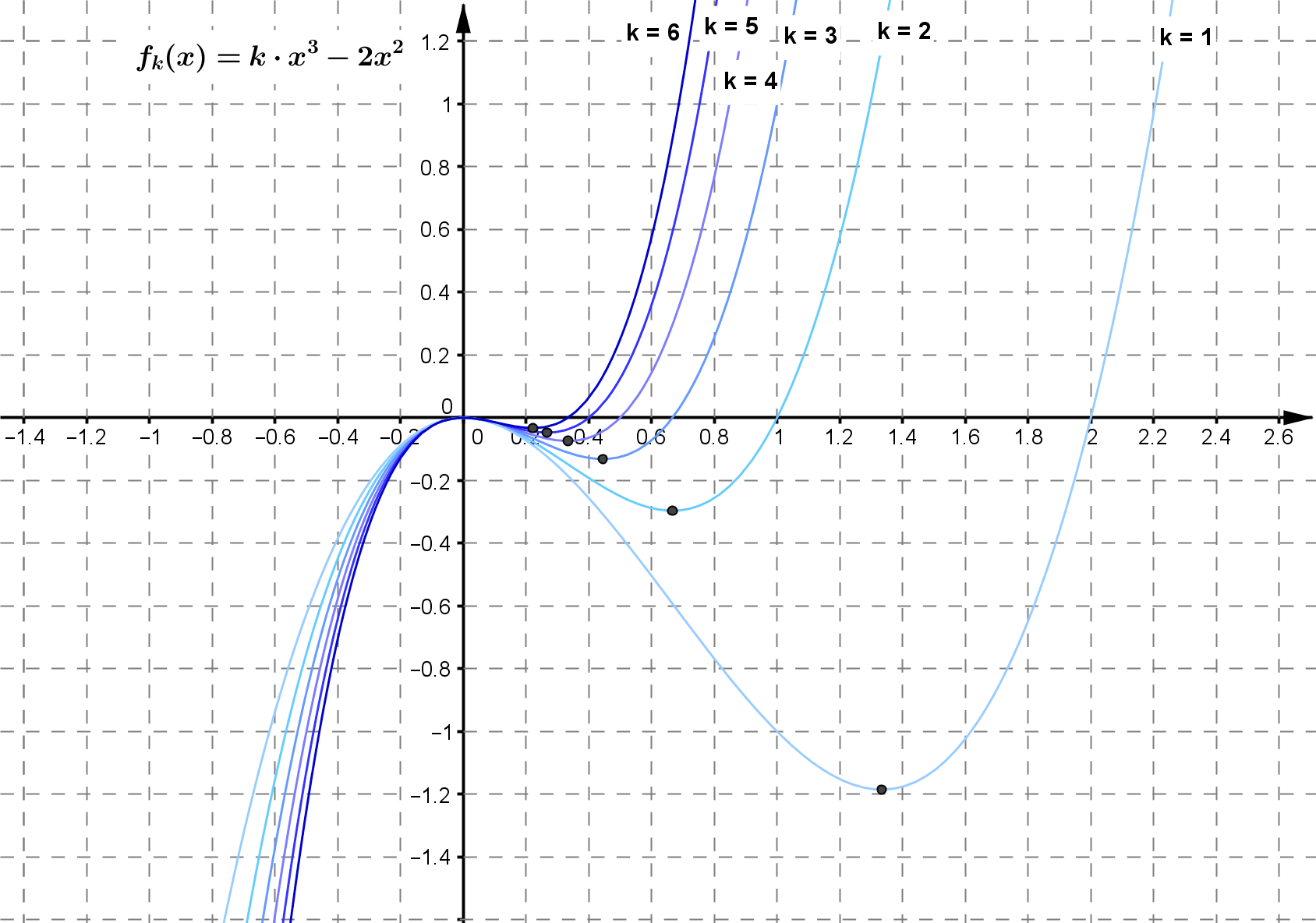
Es sei $f_k(x)= k \cdot x^3 - 2 x^2$. In der Abbildung sind die Graphen für die Werte $k = 1 \ldots 6$ gezeigt. Markiert sind die Minima der jeweiligen Funktionen. Man erkennt, dass diese Minima einem Funktionsverlauf folgen.
Bestimmung der Minima: \begin{align} f_k'(x)&= 3k \cdot x^2 - 4 x \\ f_k '(x)&=0\\ 3k \cdot x^2 - 4 x &= 0 \\ x \left( 3k \cdot x - 4 \right) &= 0 \\ x = 0 &\vee 3k \cdot x - 4 = 0 \\ x_{1} = 0 &\vee x_2 = \frac{4}{3k} \end{align} Einsetzen in die zweite Ableitung: \begin{align} f_k ''(x) &= 6k \cdot x - 4 \\ f_k '' (0) &= - 4 \quad \rightarrow \text{Maximum} \\ f_k ''\left( \frac{4}{3k} \right) &= 6k \cdot \frac{4}{3k} - 4 \\ f_k '' \left( \frac{4}{3k} \right) &= 8 - 4 = 4 \quad \rightarrow \text{Minimum} \end{align} Einsetzen in die Funktion: \begin{align} f \left( \frac{4}{3k} \right) &= k \cdot \left( \frac{4}{3k} \right)^3 - 2 \left( \frac{4}{3k} \right)^2 \\ f \left( \frac{4}{3k} \right) &= k \cdot \frac{64}{27k^3} - 2 \frac{16}{9k^2} \\ f \left( \frac{4}{3k} \right) &= \frac{64}{27k^2} - \frac{96}{27k^2} \\ f \left( \frac{4}{3k} \right) &= - \frac{32}{27k^2} \end{align}
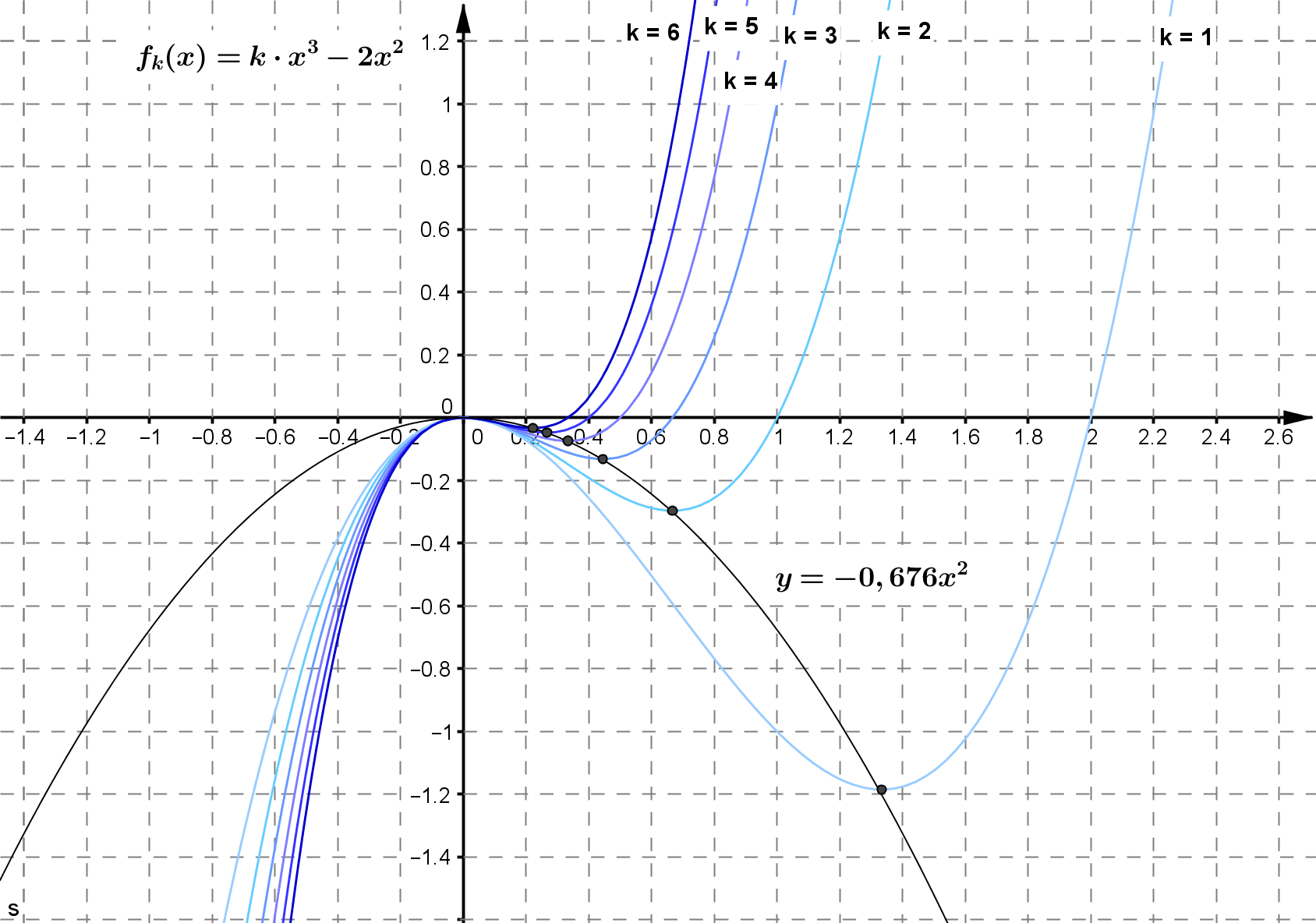Aus der $x$-Koordinate folgt:
\begin{align}
x &= \frac{4}{3k} \\
3k x &= 4 \\
k &= \frac{4}{3x}
\end{align}
Einsetzen in die $y$-Koordinate:
\begin{align}
y&= -\frac{32}{27k^2} \\
y&= -\frac{32}{27 \cdot \left( \frac{4}{3x} \right)^2} \\
y&= -\frac{32 \cdot 9 x^2}{27 \cdot 16} \\
y&= -\frac{32 x^2}{48} \\
y&= - \frac23 \cdot x^2
\end{align}
Alle Minima der Funktionsschar liegen auf der bestimmten Ortskurve.
Das Ziel einer kompletten Kurvendiskussion oder Funktionsuntersuchung ist die graphische Darstellung des Funktionsverlaufs. Mit Hilfe der bestimmten
Punkte und der gewonnenen Erkenntnisse über die Eigenschaften der Funktion kann der Funktionsgraph skizziert werden.
Mit der Skizze können dann Aussagen zu beliebigen Punkten des Graphen gemacht werden.
© mondbrand MMXIX