

 Seit Newton weiß man, dass der Naturzustand eines Körpers die gleichförmige Bewegung ist. Das ist die wesentliche Aussage aus dem
ersten Newtonschen Axiom:
Seit Newton weiß man, dass der Naturzustand eines Körpers die gleichförmige Bewegung ist. Das ist die wesentliche Aussage aus dem
ersten Newtonschen Axiom:
Lex prima (Trägheitsgesetz)
Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Translation, sofern er nicht durch einwirkende Kräfte zur Änderung seines Zustands gezwungen wird.
Der lateinische Originaltext:
Corpus omne perseverare in statu suo quiescendi vel movendi uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare.
Eine direkte Folge des ersten Axioms ist das zweite Axiom, wonach die einwirkende Kraft proportional zur Änderung der Bewegung ist:
Lex secunda (Aktionsgesetz)
Die Änderung der Bewegung einer Masse ist der Einwirkung der bewegenden Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie, nach welcher jene Kraft wirkt.
Der lateinische Originaltext:
Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum lineam rectam qua vis illa imprimitur.
Kurz: $F = m \cdot a$
Lex tertia (Wechselwirkungsgesetz)
Kräfte treten immer paarweise auf. Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio), so wirkt eine gleich große, aber entgegen gerichtete Kraft von Körper B auf Körper A (reactio).
Der lateinische Originaltext:
Actioni contrariam semper et aequalem esse reactionem: sive corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi.
Das dritte Axiom befasst sich damit, dass jede Kraft automatisch auch eine Gegenkraft bedingt. Die bekannte Formulierung actio = reactio ist insofern irreführend, da sie eine zunächst wirkende Kraft voraussetzt, auf die dann durch eine Gegenkraft reagiert wird. In Wirklichkeit wirken Kraft und Gegenkraft gleichzeitig.
Die Klassifizierung "actio" heißt vielmehr, dass diese Kraft die in der Anwendung interessierende Kraft darstellt, wohingegen die "reactio", also die Gegenkraft, im Grunde nicht interessiert bzw. sich auch nicht messbar auswirkt. Beispielsweise gibt es als "actio" die Gravitationskraft, d.h. ein Apfel wird von der Erde angezogen und in Richtung Erdmittelpunkt beschleunigt. Diese Kraft hat Auswirkungen, im wesentlichen auf den Apfel, der herunterfällt. Die "reactio" in diesem Beispiel wäre die anziehende Kraft des Apfels auf die Erde. Diese wird nämlich auch in Richtung des Apfelmittelpunkts beschleunigt, was sich aufgrund der großen Masse der Erde (2.Axiom) und deren Trägheit (1.Axiom) aber nicht bemerkbar macht.
Die Newtonschen Axiome sind die Grundpfeiler der Mechanik. Angefangen bei der gleichförmigen Bewegung als der natürliche Bewegungszustand eines Körpers, weitergehend mit der Notwendigkeit einer Kraft, um diesen Bewegungszustand zu ändern bis zu der zwingend notwendigen Gegenkraft, die gleichzeitig zu jeder wirkenden Kraft auftritt.
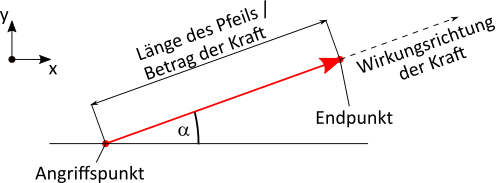 Kräfte werden als Pfeile dargestellt. Die Länge des Pfeiles entspricht dabei dem Betrag der Kraft, die Richtung, in die
der Pfeil zeigt, entspricht der Wirkungsrichtung der Kraft.
Kräfte werden als Pfeile dargestellt. Die Länge des Pfeiles entspricht dabei dem Betrag der Kraft, die Richtung, in die
der Pfeil zeigt, entspricht der Wirkungsrichtung der Kraft.
Die Wirkungsrichtung wird immer bezüglich einer positiven x-Achse gemessen. Es ist also wichtig, sich bei der
Analyse der geometrischen Situation über ein Koordinatensystem klar zu werden. In den meisten Fällen wird die
x-Achse parallel zur Erdoberfläche bzw. parallel zu einer beliebigen Oberfläche und die y-Achse senkrecht dazu festgelegt.
In dem gezeigten Beispiel wirkt die Kraft unter einem Winkel von ca. 20°. Der Betrag der Kraft kann durch Messung der Pfeillänge ermittelt werden. Dabei muss dann der verwendete Maßstab beachtet werden.
Aufteilung in definierte Richtungen
Jede Kraft kann in alle möglichen Richtungen wirken. Wenn dann auch noch mehrere Kräfte auf einen Körper wirken, wird die Berechnung der Gesamtwirkung schnell kompliziert.
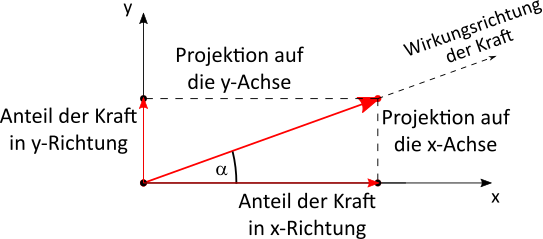
Daher wird jede beliebige Kraft zunächst in definierte Wirkungsrichtungen aufgeteilt. Diese definierten Richtungen sind die $x-$ und die $y-$Achse eines Koordinatensystems, bzw. die Richtung, in der eine Bewegung stattfinden kann und die Richtung senkrecht dazu. Wichtig ist daher, dass die definierten Wirkungslinien senkrecht zueinander sind.
Der Kraftpfeil wird auf die Koordinatenachsen projiziert. Dadurch entstehen zwei Kraftkomponenten: der Anteil der Kraft in $x-$ und in $y-$Richtung.
Berechnet werden die Anteile durch die folgenden Formeln: $$ F_x = F \cdot \cos \alpha \\ F_y = F \cdot \sin \alpha $$
Addition von Kräften
Die Addition von Kräften ist dann notwendig, wenn an einem Körper mehrere Kräfte angreifen und man die Aufgabe hat, die Gesamtwirkung, d.h die Gesamtkraft zu bestimmen. Die Gesamtkraft wird dann meist als resultierende Kraft $F_R$ bezeichnet.
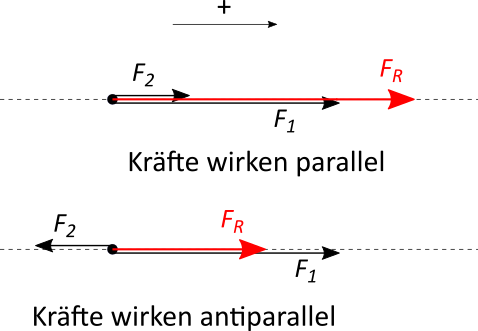
Wirken beide Kräfte auf einer Wirkungslinie, d.h. sie wirken parallel oder antiparallel, werden die Kräfte einfach addiert. Es ist dabei zu beachten, dass auch hier eine positive Richtung angenommen wird. Wirkt die Kraft in diese positive Richtung, ist sie auch positiv (z.B. $F = 8 \text{ N}$). Wirkt sie dagegen in die entgegengesetzte Richtung, ist sie negativ (z.B. $F = -3 \text{ N}$).
Ist also $F_1 = 8 \text{ N}$ und $F_2 = 3 \text{ N}$, dann ist die resultierende Kraft $F_R = 8 + 3 = 11 \text{ N}$.
Ist dagegen $F_1 = 8 \text{ N}$ und $F_2 = -3 \text{ N}$, dann ist die resultierende Kraft $F_R = 8 + (-3) = 5 \text{ N}$.
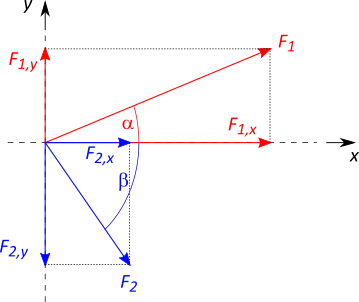
Bei beliebigen Wirkungsrichtungen wird jede Kraft zunächst in ihre $x-$ und $y-$Komponenten zerlegt. Die jeweilige $x-$Komponenten werden, da sie parallel oder antiparallel zueinander sind, einfach addiert, ebenso die jeweiligen $y-$Komponenten. Die dabei entstandenen Kraftkomponenten werden dann wieder zu einer resultierenden Kraft zusammengefasst.
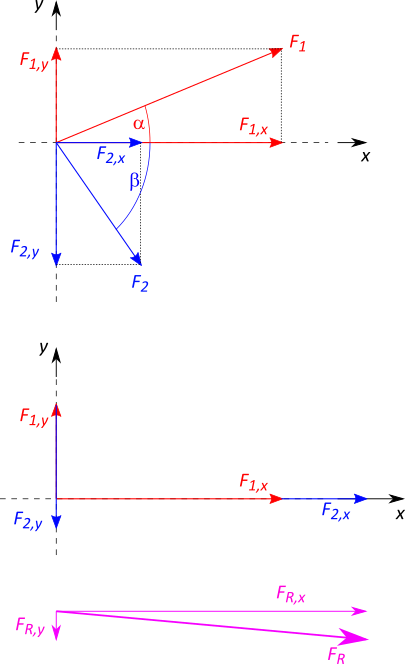
Als Beispiel seien die beiden Kräfte $F_1$ und $F_2$ gegeben, die unter dem Winkel $\alpha$ bzw. $\beta$ wirken.
\begin{align} F_{1,x} &= F_1 \cdot \cos \alpha \\ F_{1,y} &= F_1 \cdot \sin \alpha \\ \\ F_{2,x} &= F_2 \cdot \cos \beta \\ F_{2,y} &= F_2 \cdot \sin \beta \\ \\ \\ F_{R,x} &= F_1 \cdot \cos \alpha + F_2 \cdot \cos \beta \\ F_{R,y} &= F_1 \cdot \sin \alpha + F_2 \cdot \sin \beta \end{align}Um die Komponenten der resultierenden Kraft wieder zusammenzufassen, wird der Satz des Pythagoras genutzt: $$ F_R = \sqrt{\left(F_{R,x} \right)^2 + \left( F_{R,y} \right)^2} $$ Für die Richtung der resultierenden Kraft gilt: $$ \tan \vartheta = \frac{F_{R,y}}{F_{R,x}} $$
Beispiel
Zwei Kräfte greifen an einem Körper an. Die erste Kraft wirkt mit dem Betrag $F_1 = 70 \text{ N}$ unter dem Winkel $\alpha = 20°$, die zweite Kraft mit $F_2 = 40 \text{ N}$ unter $\beta = -55°$.
Dann ist
 \begin{align}
F_{1,x} &= 70 \text{ N} \cdot \cos 20° \\
F_{1,x} &= 65,78 \text{ N} \\
F_{1,y} &= 70 \text{ N} \cdot \sin 20° \\
F_{1,y} &= 23,94 \text{ N} \\ \\
F_{2,x} &= 40 \text{ N} \cdot \cos (-55°) \\
F_{2,x} &= 22,94 \text{ N} \\
F_{2,y} &= 40 \text{ N} \cdot \sin (-55°) \\
F_{2,y} &= -32,77 \text{ N} \\ \\ \\
F_{R,x} &= 65,78 \text{ N} + 22,94 \text{ N} \\
F_{R,x} &= 88,72 \text{ N} \\ \\
F_{R,y} &= 23,94 \text{ N} + \left( -32,77 \text{ N} \right) \\
F_{R,y} &= -8,83 \text{ N} \\ \\ \\
F_R &= \sqrt{\left(88,72 \text{ N} \right)^2 + \left( -8,83 \text{ N} \right)^2} \\
F_R &= 89,16 \text{ N} \\ \\
\vartheta &= \arctan \left( \frac{-8,83}{89,16} \right) \\
\vartheta &= -5,6°
\end{align}
\begin{align}
F_{1,x} &= 70 \text{ N} \cdot \cos 20° \\
F_{1,x} &= 65,78 \text{ N} \\
F_{1,y} &= 70 \text{ N} \cdot \sin 20° \\
F_{1,y} &= 23,94 \text{ N} \\ \\
F_{2,x} &= 40 \text{ N} \cdot \cos (-55°) \\
F_{2,x} &= 22,94 \text{ N} \\
F_{2,y} &= 40 \text{ N} \cdot \sin (-55°) \\
F_{2,y} &= -32,77 \text{ N} \\ \\ \\
F_{R,x} &= 65,78 \text{ N} + 22,94 \text{ N} \\
F_{R,x} &= 88,72 \text{ N} \\ \\
F_{R,y} &= 23,94 \text{ N} + \left( -32,77 \text{ N} \right) \\
F_{R,y} &= -8,83 \text{ N} \\ \\ \\
F_R &= \sqrt{\left(88,72 \text{ N} \right)^2 + \left( -8,83 \text{ N} \right)^2} \\
F_R &= 89,16 \text{ N} \\ \\
\vartheta &= \arctan \left( \frac{-8,83}{89,16} \right) \\
\vartheta &= -5,6°
\end{align}
Die resultierende Kraft wirkt mit einem Betrag von 89,16 N unter einem Winkel von -5,6°, also fast in x-Richtung.
Die Gravitation ist eine der vier fundamentalen Grundkräfte in der Physik. Sie wirkt als anziehende Kraft zwischen zwei massebehafteten Körpern. Die Kraftwirkung nimmt mit dem Quadrat des Abstands ab, reicht aber unendlich weit.
Die vier Grundkräfte
| Gravitation | Anziehungskraft zwischen Massen |
| elektromagnetische Kraft | Anziehende und abstoßende Wirkung zwischen Ladungen Aufbau der Atome |
| schwache Kernkraft | Umwandlungsprozesse innerhalb des Atomkerns |
| starke Kernkraft | anziehende Wirkung zwischen Kernbausteinen Aufbau der Atomkerne Aufbau der Elementarteilchen |
Mit Hilfe der Gravitation können die Planetenbewegungen und die Bildung und Bewegung von Galaxien beschrieben werden. Die Gravitation spielt bei Massen in der menschlichen Größenordnung, d.h. bis in den Bereich von Tonnen, keine Rolle. Die dadurch wirkenden Kräfte sind sehr klein.
Die Grundlagen zum Verständnis der Gravitation wurden bereits von Aristoteles gelegt. Altindische und persische Autoren, Kopernikus, Kepler und, nach Galilei, schließlich Newton entwickelten das Bild von der Gravitation, wie es in der klassischen Physik vorherrschend ist.
Newton entwickelte aus seinen Beobachtungen der Himmelskörper sein Gravitationsgesetz, mit dem die Bewegungen von Planeten und Sternen berechenbar geworden sind. Es lautet: $$ F = \gamma \cdot \frac{m_1 \cdot m_2}{r^2} $$ Dabei ist $\gamma$ die Gravitationskonstante mit dem Wert $\gamma = 6,673 \cdot 10^{-11} \; \frac{\text{m}^3}{\text{kg} \cdot \text{s}^2}$. $m_1$ und $m_2$ sind die aufeinander wirkenden Massen, $r$ ist der Abstand der Massenmittelpunkte voneinander.
Beispiele
Die Massen von Erde und Sonne sind $m_E = 5,976 \cdot 10^{24} \text{ kg}$ bzw. $m_S = 2 \cdot 10^{30} \text{ kg}$, der mittlere Abstand Erde-Sonne beträgt $r = 149,6 \cdot 10^9 \text{ m}$. Damit beträgt die Kraft aufgrund der Gravitation \begin{align} F &= \gamma \cdot \frac{m_1 \cdot m_2}{r^2} \\ \\ F &= 6,673 \cdot 10^{-11} \; \frac{\text{m}^3}{\text{kg} \cdot \text{s}^2} \cdot \frac{5,976 \cdot 10^{24} \text{ kg} \cdot 2 \cdot 10^{30} \text{ kg}}{\left(149,6 \cdot 10^9 \text{ m}\right)^2} \\ \\ F &= 3,56 \cdot 10^{22} \text{ N} \end{align}
Die Gewichtskraft, die auf einen Körper wirkt, ist nun diejenige Kraft, die durch die Gravitation hervorgerufen wird. Man kann das Gravitationsgesetz folgendermaßen umstellen: \begin{align} F &= \gamma \cdot \frac{m_1 \cdot m_2}{r^2} \\ F &= \frac{\gamma \cdot m_1}{r^2} \cdot m_2 \end{align} Mit den Größen $m_1$ als die Masse der Erde und $r$ als den Erdradius kann man den Vorfaktor $\frac{\gamma \cdot m_1}{r^2}$ als Konstante für den Ort der Kraftmessung ansehen und zusammenfassen. Man schreibt dann $$ F_G = g \cdot m_2 $$ bzw. $$ F_G = m \cdot g $$ für die Gewichtskraft $F_G$, die am Ort mit der Konstanten $g$ auf den Körper mit der Masse $m$ wirkt. $g$ wird auch als Ortsfaktor bezeichnet. Da $g$ auch eine Beschleunigung darstellt, wird es auch als Fallbeschleunigung bezeichnet.
| Mitteleuropa | $9,81 \; \frac{\text{m}}{\text{s}^2}$ |
| Äquator | $9,79 \; \frac{\text{m}}{\text{s}^2}$ |
| Pol | $9,83 \; \frac{\text{m}}{\text{s}^2}$ |
| Mond | $1,62 \; \frac{\text{m}}{\text{s}^2}$ |
| Mars | $3,71 \; \frac{\text{m}}{\text{s}^2}$ |
| Jupiter | $24,79 \; \frac{\text{m}}{\text{s}^2}$ |
Etwas genauer betrachtet, muss man berücksichtigen, dass die Verteilung der Masse innerhalb der Erde unregelmäßig ist. Die idealisierte Form einer punktförmigen Masse ist natürlich nicht vorhanden. Dafür gibt es widerum modellhafte Vorstellungen, z.B. das PREM, ein Referenzmodell für einige physikalische Parameter im Erdinneren.
Weiterhin muss beachtet werden, dass z.B. durch die Erdrotation jeder Körper an der Oberfläche durch Fliehkräfte nach außen, also entgegen der Gravitation bewegt werden.
Messungen des Ortsfaktors entsprechen daher selten den theoretischen Werten. Für Mitteleuropa würde etwa theoretisch gelten: \begin{align} g_{theo} &= \frac{\gamma \cdot m_1}{r^2} \\ \\ g_{theo} &= \frac{6,673 \cdot 10^{-11} \; \frac{\text{m}^3}{\text{kg} \cdot \text{s}^2} \cdot 5,976 \cdot 10^{24} \text{ kg}}{(6365000 \text{ m})^2} \\ g_{theo} &= 9,84 \; \frac{\text{m}}{\text{s}^2} \end{align}
Die Gewichtskraft bewirkt, dass jeder Körper immer in Richtung des Erdmittelpunkts gezogen wird. Wenn der Körper frei fällt, wird er mit der Beschleunigung $g$ fallen.
 Mit Hilfe der schiefen Ebene kann illustriert werden, wie und vor allem warum eine Kraft in zwei Teile aufgeteilt wird.
Mit Hilfe der schiefen Ebene kann illustriert werden, wie und vor allem warum eine Kraft in zwei Teile aufgeteilt wird.
Für gerichtete Größen wie die Kraft, aber auch für die Geschwindigkeit oder die Beschleunigung, sind zwei Richtungen wesentlich: Erstens die Richtung, in der eine Bewegung oder eine Wirkung stattfindet bzw. stattfinden soll und zweitens die Richtung senkrecht dazu.
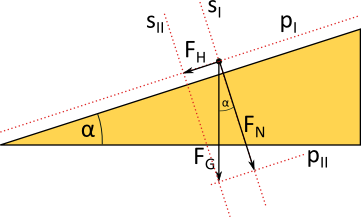
Bei der schiefen Ebene ist das erstens die Richtung parallel zur Ebene (die Richtung, in der eine Bewegung abläuft) und die Richtung senkrecht dazu. In der Skizze ist der Massepunkt, der den Körper symbolisiert, der Ausgangspunkt für zunächst einmal die Gewichtskraft $F_G$. Die Länge des Kraftpfeils entspricht dem Betrag der Gewichtskraft. Sie ist die einzig wirkende Kraft in dieser Situation. Die Richtung parallel zur Ebene wird durch die rot punktierte Linie $p_I$ dargestellt, die Richtung senkrecht dazu durch die Linie $s_I$. Beide Linien verlaufen durch den Massepunkt.
Durch den Endpunkt des Gewichtskraftpfeils wird nun noch eine Linie $p_{II}$ parallel zur Ebene gezeichnet, genauso wie eine Linie $s_{II}$ senkrecht dazu. Insgesamt entsteht so ein rot punktiertes Rechteck mit dem Gewichtskraftpfeil als eine der Diagonalen.
Der Winkel $\alpha$ bezeichnet den Neigungswinkel, den die Ebene bezüglich der waagerechten Unterlage (der Erdoberfläche) aufweist. Der Winkel taucht in dem rot punktierten Rechteck wieder auf zwischen dem Gewichtskraftpfeil und den Linien $s_I$ (oben rechts) bzw. $s_{II}$ (unten links).
Die beiden in das Rechteck eingezeichneten Kräfte $F_H$ und $F_N$ sind nun die beiden Kräfte, die in die Bewegungs- oder Wirkungsrichtung $\left( F_H \right)$ bzw. senkrecht auf die Ebene $\left( F_N \right)$ zeigen. Berechnet werden sie durch die folgenden Gleichungen: $$ F_H = F_G \cdot \sin \alpha \\ \\ F_N = F_G \cdot \cos \alpha $$
Die Kraft $F_H$ wird Hangabtriebskraft genannt, also ist es die Kraft, die dafür sorgt, dass die Bewegung entlang der Ebene nach unten verläuft. Für die Kraft $F_N$ wird die Bezeichnung Normalkraft genutzt. (Mathematisch ist die Normale allerdings eine Richtung, die senkrecht von einer Ebene wegzeigt. Die Normalkraft zeigt hingegen auf die Ebene, ist also genau entgegengesetzt. Unbeachtet der Tatsache hat sich aber die Bezeichnung in der Physik eingebürgert. Wichtig ist damit die Wirkungsrichtung, die senkrecht zu einer Oberfläche ist.) Die Normalkraft sorgt dafür, dass der Körper auf die Oberfläche gedrückt wird. Es ist also so etwas wie eine Andruckkraft.
Die Wirkung von $F_H$ ist dann z.B. eine Beschleunigung einer Bewegung. $F_N$ wirkt indirekt als Reibkraft, die eine Bewegung behindert bzw. verhindert. Das wird im Abschnitt über die Reibung erläutert.
Eine Bewegung ist gekennzeichnet durch die Geschwindigkeit $v = \frac{\Delta s}{\Delta t}$. Ist der in einer Zeitspanne $\Delta t$ zurückgelegte Weg $\Delta s$ konstant, spricht man von einer gleichförmigen Bewegung. Soll sich die Bewegung und damit die Geschwindigkeit ändern, muss eine Beschleunigung $a = \frac{\Delta v}{\Delta t}$ vorhanden sein. Mit dem zweiten Newtonschen Axiom $F=m \cdot a$ führt das zu einer Kraft, die damit für die Bewegungsänderung des betrachteten Körpers sorgt.
Beispiel 1
Ein Auto mit der Masse $m = 1200 \text{ kg}$ beschleunigt von 0 auf 100 km/h in $t = 8 \text{ s}$. Bestimmt werden soll die Beschleunigungskraft des Motors.
Ansatz:
Am Ende soll die Kraft berechnet werden, also $F = m \cdot a$. Die Masse ist bekannt, die Beschleunigung nicht. Aber es gilt:
$a = \frac{\Delta v}{\Delta t}$.
Da $\Delta t$ bekannt ist (8 s), muss nur noch $\Delta v$ bestimmt werden: \begin{align} \Delta v &= 100 - 0 \; \frac{\text{km}}{\text{h}} \\ \Delta v &= \frac{100}{3,6} \; \frac{\text{m}}{\text{s}} \\ \Delta v &= 27,78 \; \frac{\text{m}}{\text{s}} \end{align} Es folgt insgesamt: \begin{align} F &= m \cdot a \\ F &= m \cdot \frac{\Delta v}{\Delta t} \\ F &= 1200 \; \text{kg} \cdot \frac{28,78 \; \frac{\text{m}}{\text{s}}}{8 \; \text{s}} \\ F &= 4167 \; \text{N} \\ \\ F &\approx 4,17 \; \text{kN} \end{align} Das Auto wird also mit ungefähr 4,17 kN angetrieben.
Beispiel 2
Das Auto soll nun abgebremst werden. Zum Bremsen steht eine Kraft von $F = 10000 \; \text{N}$ zur Verfügung. Die Frage ist, welchen Weg das Auto noch zurücklegt, wenn es sich mit $v = 50 \; \frac{\text{km}}{\text{h}}$ bewegt.
Ansatz:
Es gilt $F = m \cdot a$. Für die beschleunigte Bewegung gelten die beiden Zusammmenhänge: (I) $s = \frac12 a \cdot t^2$ und (II) $v = a \cdot t$.
Fasst man die beiden Gleichungen zusammen, erhält man
\begin{align}
s &= \frac12 a \cdot t^2 &\qquad \qquad v &= a \cdot t \\ \\
s &= \frac12 a \cdot t^2 &\qquad \qquad t &= \frac{v}{a} \\ \\
s &= \frac12 a \cdot \frac{v^2}{a^2} \\ \\
s &= \frac{v^2}{2a}
\end{align}
Mit $a = \frac{F}{m}$ führt das zu der Berechnung:
\begin{align}
s &= \frac{v^2 \cdot m}{2F} \\ \\
s &= \frac{\left( \frac{50}{3,6} \; \frac{\text{m}}{\text{s}} \right)^2 \cdot 1200 \; \text{kg}}{2 \cdot 10000 \; \text{N}} \\ \\
s &= 11,574 \; \text{m}
\end{align}
Es fährt also noch gut 11,6 m bis zum Stillstand.
Die Reibungskraft sorgt immer und in jedem Fall dafür, dass Bewegungen abgebremst werden.
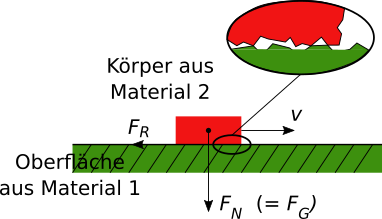
In der Abbildung wird die Bewegung mit der Geschwindigkeit $v$ durch die Reibkraft $F_R$ abgebremst.
Die Reibungskraft entsteht durch die mikroskopische Gestalt der beiden Kontaktflächen, die sich ineinander verhaken, wenn sich die Oberflächen
gegeneinander bewegen. Die Kraft, die den Körper auf die Oberfläche drückt, wird Normalkraft $F_N$ genannt, in Anlehnung an den mathematischen
Begriff der Normalen, der Richtung senkrecht zu Oberflächen. Die Form der Kontaktflächen, die Materialien von Körper und Oberfläche sowie
der Zustand der Kontaktflächen (nass, trocken, geschmiert, ...) definieren, wie die Normalkraft als Reibungskraft wirkt.
Aus der Gewichtskraft, die immer in Richtung Erdmittelpunkt wirkt, wird die Normalkraft bestimmt:
$$
F_N = F_G \cdot \cos \alpha
$$
Aus der Normalkraft wird die Reibungskraft bestimmt:
$$
F_R = \mu \cdot F_N
$$
Insgesamt erhält man somit:
$$
F_R = m \cdot g \cdot \mu \cdot \cos \alpha
$$
mit $\mu$ als dem sogenannten Reibkoeffizienten, der die Materialpaarung und die Kontakteigenschaften berücksichtigt. Der Winkel $\alpha$ ist
der Neigungswinkel der Oberfläche zur Waagerechten (dazu: Schiefe Ebene).
Die Reibungskraft wirkt als Bremskraft analog zu der Beschleunigungskraft.
Für eine etwas detailliertere Betrachtung der Reibung müssen drei unterschiedliche Szenarien betrachtet werden:
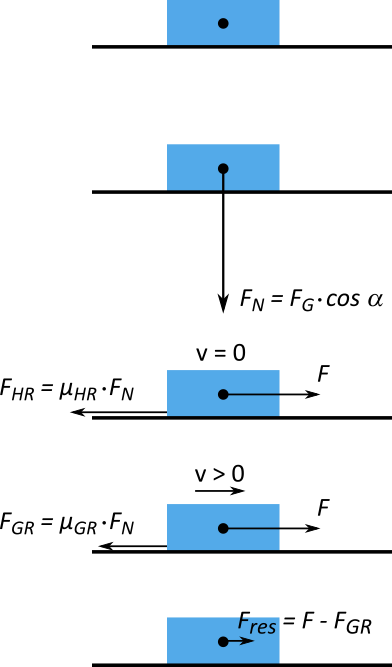
Fall I: Haftreibung
Um einen Körper überhaupt aus dem Stillstand in eine Bewegung zu versetzen, muss die sogenannte Haftreibung überwunden werden. Der Haftreibungskoeffizient wird mit $\mu_{HR}$ bezeichnet.
Für die Haftreibungskraft gilt: $$ F_{HR} = m \cdot g \cdot \mu_{HR} \cdot \cos \alpha \\ F_{HR} = F_N \cdot \mu_{HR} $$
Fall II: Gleitreibung
Ist der Körper bereits in Bewegung, wirkt nur noch die Gleitreibung mit dem Gleitreibungskoeffizienten $\mu_{GR}$. Es ist zu beachten, dass die Gleitreibung sofort einsetzt, wenn der Körper sich bewegt. Der Übergang zwischen Haft- und Gleitreibung geschieht sofort.
Für die Gleitreibungskraft gilt: $$ F_{GR} = m \cdot g \cdot \mu_{GR} \cdot \cos \alpha \\ F_{GR} = F_N \cdot \mu_{GR} $$
| Materialpaarung | $\mu_{HR}$ | $\mu_{GR}$ | $\mu_{RR}$ in cm |
| Stahl auf Stahl | 0,15 | 0,03 - 0,09 | - |
| Stahl auf Eis | 0,03 | 0,01 | - |
| Gummireifen auf Asphalt, trocken | < 0,9 | < 0,3 | 0,002 |
| Gummireifen auf Asphalt, nass | < 0,5 | < 0,15 | - |
| Holz auf Holz | 0,5 - 0,65 | 0,2 - 0,4 | - |
| Stahlreifen auf Schienen | 0,15 | 0,03 - 0,09 | 0,006 |
Weitere Beispiele für Reibkoeffizienten gibt es hier.
Fall III: Rollreibung
Die Rollreibung mit dem Rollreibungskoeffizienten $\mu_{RR}$ wirkt, wenn ein Körper über die Oberfläche abrollt. Im Gegensatz zu $\mu_{HR}$ und $\mu_{GR}$ ist $\mu_{RR}$ eine Größe mit einer Einheit. Es gilt $\left[ \mu_{RR} \right] = 1 \text{ cm}$. Die Rollreibungskraft wird auf den Radius des rollenden Körpers bezogen und wird damit immer kleiner, je größer der Radius ist.
Für die Rollreibungskraft gilt: $$ F_{RR} = \frac{ m \cdot g \cdot \mu_{RR} \cdot \cos \alpha }{r} \\ F_{RR} = \frac{F_N}{r} \cdot \mu_{RR} $$
Es gilt immer $\mu_{HR} > \mu_{GR} > \mu_{RR}$.
Das bedeutet, dass die Haftreibung stärker ist als die Gleitreibung, die wiederum stärker ist als die Rollreibung.
Beispiele
Ein Körper aus Holz mit der Masse $m = 2 \text{ kg}$ befindet sich in Ruhe auf einer ebenen Holzoberfläche. Die Haftreibungskraft
ist
\begin{align}
F_{HR} &= m \cdot g \cdot \mu_{HR} \cdot \cos \alpha \\ \\
F_{HR} &= 2 \text{ kg} \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot 0,6 \cdot \cos 0° \\
F_{HR} &= 11,772 \text{ N}
\end{align}
 Es wurde ein mittlerer Reibkoeffizient aus dem Bereich zwischen 0,5 und 0,65 gewählt.
Es wurde ein mittlerer Reibkoeffizient aus dem Bereich zwischen 0,5 und 0,65 gewählt.
Wenn mindestens diese Kraft wirkt, setzt sich der Holzkörper in Bewegung. Bewegt er sich, wirkt aber die etwas kleinere Gleitreibungskraft: \begin{align} F_{GR} &= m \cdot g \cdot \mu_{GR} \cdot \cos \alpha \\ \\ F_{GR} &= 2 \text{ kg} \cdot 9,81 \; \frac{\text{m}}{\text{s}^2} \cdot 0,3 \cdot \cos 0° \\ F_{GR} &= 5,886 \text{ N} \end{align} Diese Kraft ist notwendig, um den Körper in gleichförmiger Bewegung zu halten. Jede andere Kraft beschleunigt ihn.
Wenn also bei einem sich bewegenden Körper immer noch die Kraft wirkt, die ihn in Bewegung versetzte, verbleibt eine resultierende Kraft, die den Körper positiv beschleunigt. Hier also \begin{align} F_{res} &= F - F_{GR} \\ F_{res} &= 11,772 \text{ N} - 5,886 \text{ N} = 5,886 \text{ N} \end{align} Nun kann man mit $F = m \cdot a$ und den Bewegungsgleichungen die weitere Bewegung des Körpers beschreiben.
Ist die Kraft, die an dem Körper wirkt, kleiner als die Gleitreibungskraft, wird der Körper ebenfalls beschleunigt, nur eben negativ, also wird der Körper abgebremst.
Ein Körper aus Stahl liegt auf einer um $\alpha$ geneigten Holzrampe. Die Masse des Körpers beträgt $m = 3 \text{ kg}$. Ein Frage könnte sein, bei welchem Winkel der Körper anfängt zu rutschen.
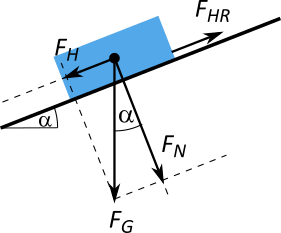
Da der Körper liegt, wird $\mu_{HR}$ benötigt. Ein mittlerer Wert ist $\mu_{HR} = 0,6$. Die Oberfläche ist geneigt, also muss die Normalkraft $F_N$ ermittelt werden. Es ist $F_N = F_G \cdot \cos \alpha$. Damit bekommt man die Haftreibungskraft $F_{HR} = \mu_{HR} \cdot F_N$. Für ein eventuelles Rutschen wäre die Hangabtriebskraft $F_H = F_G \cdot \sin \alpha$ verantwortlich. Das Rutschen fängt dann an, wenn gilt: $$ F_H > F_{HR} \\ F_G \cdot \sin \alpha > F_G \cdot \cos \alpha \cdot \mu_{HR} \\ \sin \alpha > \cos \alpha \cdot \mu_{HR} \\ \tan \alpha > \mu_{HR} $$ Damit gilt für den Winkel: $$ \alpha = \tan^{-1} \left(\mu_{HR} \right) \\ \alpha = \tan^{-1} \left(0,6\right) \\ \alpha = 30,96° $$ Bei ca. 31° Neigung fängt der Stahlkörper an zu rutschen.
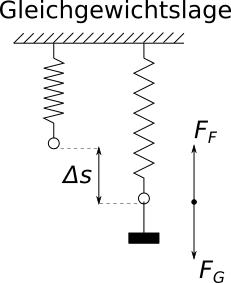 Wird ein Körper mit einer Masse $m$ an eine Feder gehängt, verlängert sich die Feder um einen bestimmten Weg $s$. Die Verlängerung ist
proportional zur angehängten Masse und wegen $F_G = m \cdot g$ auch proportional zur Gewichtskraft.
Wird ein Körper mit einer Masse $m$ an eine Feder gehängt, verlängert sich die Feder um einen bestimmten Weg $s$. Die Verlängerung ist
proportional zur angehängten Masse und wegen $F_G = m \cdot g$ auch proportional zur Gewichtskraft.
Wenn der Körper an die Feder gehängt wird, befindet er sich nach einer Weile in Ruhe. Dann wirkt insgesamt keine resultierende Kraft auf ihm.
Die Gewichtskraft wird durch die Kraft, die die Feder ausübt ($F_F$), ausgeglichen: $F_G = - F_F$. Das System befindet sich im Gleichgewicht und
es gilt $s \sim - F_F$.
Die Federkraft ist die Kraft, mit der die Feder versucht, ihre aufgezwungene Verlängerung rückgängig zu machen. Da die
Feder aber natürlich nicht agieren kann, sondern nur auf die Belastung durch die Masse des angehängten Körpers reagiert, führt das dazu, dass die
Federkraft so groß ist, dass sie die Gewichtskraft gerade ausgleicht. Die Feder wird also nicht weiter verlängert und befindet sich in einer
Gleichgewichtslage.
Für die Ermittlung des Proportionaltätsfaktors wird eine beispielhafte Feder mit unterschiedlichen Massen belastet und die jeweilige Verlängerung notiert. Es entsteht z.B. die folgende Tabelle:
| Masse in kg |
Federkraft in N |
Verlängerung in m |
|---|---|---|
|
0,05 0,10 0,15 0,20 0,25 |
0,4905 0,9810 1,4715 1,9620 2,4525 |
0,090 0,182 0,270 0,363 0,451 |


Wichtig ist vor allem die Feststellung, dass die Feder eine Kraft ausübt, die sich der Verlängerung bzw. der Verkürzung der Feder entgegenstellt. Daher kommt das Minuszeichen. Die Größe der Kraft ist dabei nicht konstant, sondern hängt von der Größe der Verlängerung / Verkürzung ab.
Dieser Zusammenhang gilt nicht nur für Federn an sich, sondern für alle federnden bzw. elastischen Systeme. In bestimmten Bereichen ist z.B. auch ein Stahlstab elastisch: ein Stahlstab mit einem Querschnitt von einem Quadratmillimeter kann sich bei einer Belastung von ca. 1000 N um etwa 2 % elastisch verlängern. Die Werte hängen natürlich von der Stahlsorte und von der Herstellung / Behandlung des Stahls ab und sind lediglich beispielhaft zu verstehen.
Beispiel
Eine Feder wird durch eine Masse von 5 kg belastet und verlängert sich dabei um 5 cm. Bestimmt werden soll die Federkonstante.
Ansatz:
Es gilt $F = D \cdot s$. Umgeformt: $D = \frac Fs$
\begin{align}
D &= \frac{m \cdot g}{s} \\ \\
D&= \frac{5 \; \text{kg} \cdot 9,81 \; \frac{\text{m}}{\text{s}^2}}{0,05 \; \text{m}} \\ \\
D&= 981 \; \frac{\text{N}}{\text{m}}
\end{align}
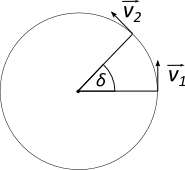 Bei der Bewegung im Kreis muss man unterscheiden zwischen der Bewegung entlang der kreisförmigen Bahn und der Bewegung, die das Objekt immer
wieder auf die Kreisbahn zwingt.
Bei der Bewegung im Kreis muss man unterscheiden zwischen der Bewegung entlang der kreisförmigen Bahn und der Bewegung, die das Objekt immer
wieder auf die Kreisbahn zwingt.
Zur Klärung: Jede Bewegung, auf die keine Kräfte wirkt, ist konstant. Das heißt, dass es keine Geschwindigkeitveränderung
und auch keine Richtungsveränderung gibt. Jedes Objekt ohne Krafteinwirkung wird sich also mit konstanter Geschwindigkeit in einer geraden Linie
weiter bewegen. Beschreibt das Objekt aber eine Kreisbahn, gibt es eine Richtungsänderung, also muss auch eine Beschleunigung existieren, die diese
Richtungsänderung bewirkt.
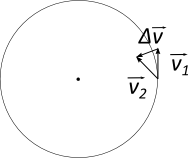
Das $\Delta v$ bezeichnet hier die benötigte Geschwindigkeitsänderung, damit das Objekt auf der Kreisbahn bleibt.
Trägt man nicht die Geschwindigkeiten auf sondern den zurückgelegten Weg, erhält man die untenstehende Abbildung. Dort wird der Weg, den das Objekt an dem Punkt $P_1$ im Zeitintervall $\Delta t$ zurücklegen würde, mit $s_1$ bezeichnet. Es ist zu beachten, dass die Bewegung entlang der Kreisbahn gleichförmig ist.
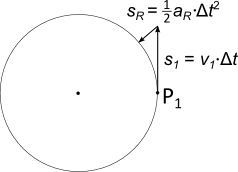 $s_R$ ist die Bezeichnung für den dann notwendigen Weg
zurück auf die Kreisbahn. Die Richtung von $s_R$ ist senkrecht zur Kreisbahn bzw. genau auf den Kreismittelpunkt. Da es sich hier um eine
Richtungsänderung der Bewegung handelt, ist diese Bewegung eine gleichmäßig beschleunigte Bewegung.
$s_R$ ist die Bezeichnung für den dann notwendigen Weg
zurück auf die Kreisbahn. Die Richtung von $s_R$ ist senkrecht zur Kreisbahn bzw. genau auf den Kreismittelpunkt. Da es sich hier um eine
Richtungsänderung der Bewegung handelt, ist diese Bewegung eine gleichmäßig beschleunigte Bewegung.
Werden die beiden eingezeichneten Wege jeweils ergänzt durch den Radius des Kreises ergibt sich ein rechtwinkliges Dreieck. Für dieses muss der Satz
des Pythagoras gelten, also:
$$
r^2 + \left( v_1 \cdot \Delta t \right)^2 = \left( r + \frac{1}{2} a_R \cdot \Delta t^2 \right)^2
$$
 Rechts von Gleichheitszeichen steht eine binomische Formel. Multipliziert man diese aus, erhält man den folgenden Ausdruck:
$$
r^2 + v_1^2 \cdot \Delta t^2 = r^2 + 2 \cdot r \cdot \frac{1}{2} a_R \cdot \Delta t^2 + \frac{1}{4} a_R^2 \cdot \Delta t^4
$$
Der Term $r^2$ steht auf beiden Seiten der Gleichung und kürzt sich heraus. Desweiteren gibt es in jedem Summanden den Term $\Delta t^2$, der ebenfalls
herausgekürzt wird. Es entsteht die Gleichung:
$$
v_1^2 = 2 \cdot r \cdot \frac{1}{2} a_R + \frac{1}{4} a_R^2 \cdot \Delta t^2
$$
Da eine Bewegung auf einer Kreisbahn nicht in einem Sägezahnmuster abläuft, sondern
eine kontinuierliche Bewegung ist, wird der Term $\Delta t = 0$ gesetzt.
Rechts von Gleichheitszeichen steht eine binomische Formel. Multipliziert man diese aus, erhält man den folgenden Ausdruck:
$$
r^2 + v_1^2 \cdot \Delta t^2 = r^2 + 2 \cdot r \cdot \frac{1}{2} a_R \cdot \Delta t^2 + \frac{1}{4} a_R^2 \cdot \Delta t^4
$$
Der Term $r^2$ steht auf beiden Seiten der Gleichung und kürzt sich heraus. Desweiteren gibt es in jedem Summanden den Term $\Delta t^2$, der ebenfalls
herausgekürzt wird. Es entsteht die Gleichung:
$$
v_1^2 = 2 \cdot r \cdot \frac{1}{2} a_R + \frac{1}{4} a_R^2 \cdot \Delta t^2
$$
Da eine Bewegung auf einer Kreisbahn nicht in einem Sägezahnmuster abläuft, sondern
eine kontinuierliche Bewegung ist, wird der Term $\Delta t = 0$ gesetzt.
Somit erhält man: \begin{align} v_1^2 & = 2 \cdot r \cdot \frac{1}{2} a_R \\ v_1^2 & = r \cdot a_R \\ a_R & = \frac{v_1^2}{r} \end{align} Da die Bedingung für $a_R$ natürlich zu jedem Zeitpunkt und für jeden Punkt auf der Kreisbahn gilt, folgt: $$ a_R = \frac{v^2}{r} \quad \text{oder} \quad a_Z = \frac{v^2}{r} $$ Diese Größe nennt man Radialbeschleunigung oder Zentripetalbeschleunigung und ist notwendig, wenn es eine Kreisbewegung geben soll. Die Einheit ist wie bei der (Bahn-)Beschleunigung Meter pro Sekunde zum Quadrat. $$ \text{Radialbeschleunigung} \; a_R \\ \text{Zentripetalbeschleunigung} \; a_Z \\ [a_Z] = 1 \; \frac{ \text{m}}{ \text{s}^2} $$
Nach dem zweiten Newtonschen Axiom gilt: $$ F = m \cdot a $$ Mit der Zentripetalbeschleunigung $a_Z$ gibt es also eine Zentripetalkraft $F_Z$ (bzw. eine Zentralkraft oder Radialkraft), für die gilt: $$ F_Z = m \cdot a_Z $$ Also: $$ \text{Zentripetalkraft} \; F_Z \\ [F_Z] = 1 \; \text{N} $$ Wie schon bei der Zentripetalbeschleunigung ist die Zentripetalkraft notwendig, damit eine Kreisbewegung stattfinden kann.
© mondbrand MMXX