

Mit der Hilfe von linearen Funktionen können Geraden beschrieben und proportionale Zusammenhänge deutlich gemacht werden. Die allgemeine Form einer linearen Funktion ist:
$$ f(x) = m \cdot x + b $$ Neben dieser allgemeinen Form gibt es noch weitere Darstellungsmöglichkeiten, auf die am Rande auch eingegangen wird.Die einzelnen Bestandteile des Funktionsterms sind neben der Variablen $x$ und dem dazugehörigen Funktionswert $f(x)$ die Steigung $m$ und der $y$-Achsenabschnitt $b$.
Der Betrag der Steigung $m$ gibt an, um wieviel der Graph der Funktion ansteigt, wenn die Variable sich um eine Einheit vergrößert. Der $y$-Achsenabschnitt $b$ bezeichnet den Schnittpunkt des Graphen mit der $y$-Achse. Gilt $b = 0$, so stellt die Funktion eine Proportionalität dar: der Graph verläuft durch den Koordinatenursprung.
Eine lineare Funktion ist eindeutig definiert, wenn zwei Punkte der Funktion bekannt sind. Mit den Koordinaten $x_1, y_1$ und $x_2, y_2$ der beiden Punkte $P_1$ und $P_2$ lässt sich die allgemeine Funktionsgleichung aufstellen.

Es sind die beiden Punkte $P_1$ und $P_2$ gegeben. Die Koordinaten sind: \begin{align} P_1 &\left(-2 \mid -1 \right) \\ P_2 &\left( 4 \mid 1 \right) \end{align} also $x_1 = -2$, $y_1 = -1$ und $x_2 = 4$, $y_2 = 1$.
Durch die gegebenen Punkte verläuft die Gerade $g_1$. Mit ihr folgt die Geradengleichung: \begin{align} g_1: y = m \cdot x + b \end{align}
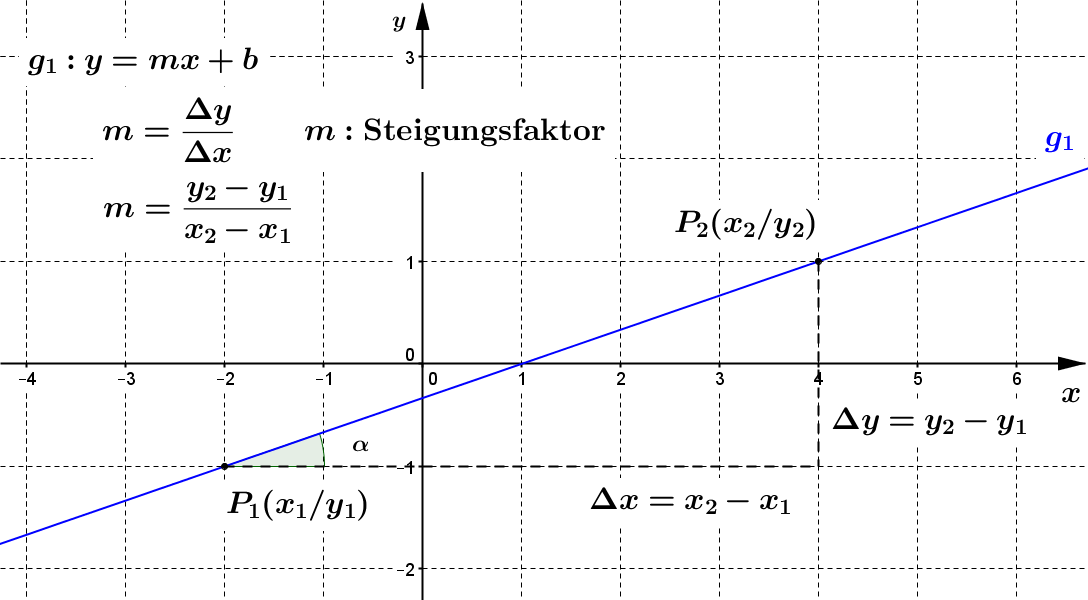
Die Steigung eines Graphen ist bestimmt durch den Quotienten aus der Differenz der $y$-Koordinaten und der Differenz der $x$-Koordinaten zweier Punkte. Im Beispiel hieße das: \begin{align} m &= \frac{\Delta y}{\Delta x} = \frac{y_2 - y_1}{x_2 - x_1} \\ \\ m &= \frac{1 - (-1)}{4 - (-2)} = \frac{2}{6} \\ \\ m &= \frac{1}{3} \end{align}
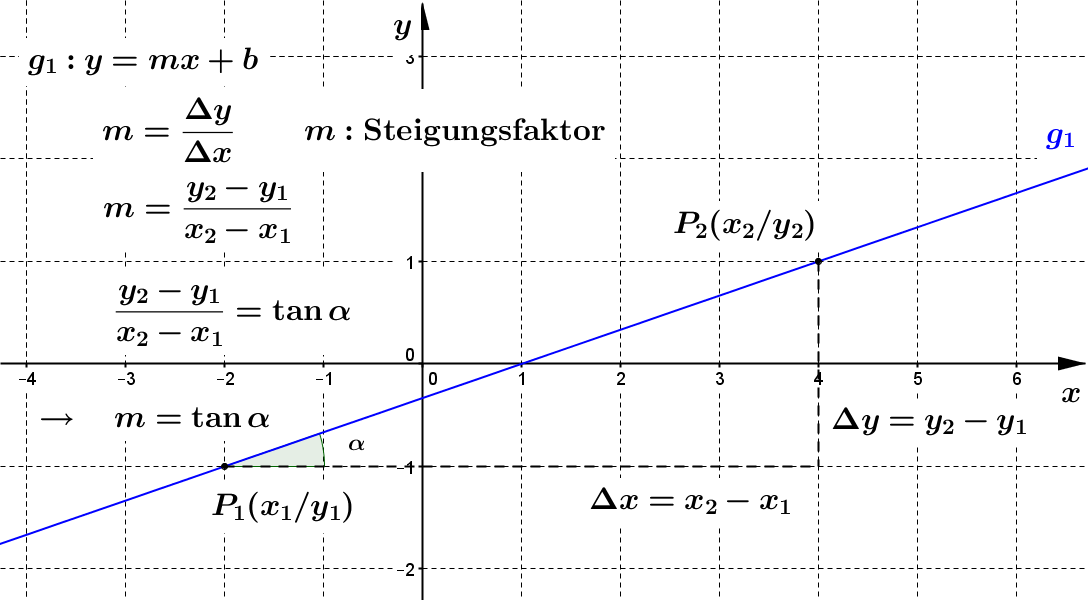
Das sogenannte Steigungsdreieck ermöglicht es immer, die Steigung einer direkten Verbindungslinie (= Gerade) zwischen zwei Punkten zu bestimmen. Die Aussage der Steigung $m = \frac{1}{3}$ ist, dass man drei Einheiten nach rechts und eine Einheit nach oben gehen muss, um von einem Punkt auf einen anderen Punkt des Graphen zu kommen. Das gleich gilt natürlich auch für vielfache von 3 bzw. 1.
Der Quotient aud $\Delta y$ und $\Delta x$ im (rechtwinkligen) Steigungsdreieck ist auch der Tangens des (Steigungs-)Winkels $\alpha$. $$ m = \tan \alpha $$
Also folgt: \begin{align} \tan \alpha &= \frac{1}{3} \\ \alpha &= \tan^{-1} \left( \frac{1}{3} \right) \\ \alpha &= 18,4\text{°} \end{align} Der Graph steigt also um 18,4° an.
Mit der bekannten Steigung $m$ und einem bekannten Punkt $P$ kann man nun den unbekannten Achsenabschnitt $b$ bestimmen: \begin{align} y &= m \cdot x + b \\ y &= \frac{1}{3} \cdot x + b \quad \text{mit} \quad P_2 \left( 4 \mid 1 \right) \\ 1 &= \frac{1}{3} \cdot 4 + b \\ b &= 1 - \frac{4}{3} \\ b &= - \frac{1}{3} \end{align}
Damit erhält man die Funktionsgleichung des oben abgebildeten Graphen: $$ y = \frac{1}{3} \cdot x - \frac{1}{3} $$
Gegeben sind die Punkte $P \left( 0 \mid 2 \right)$ und $Q \left( 3 \mid -1 \right)$.
Aus $m = \frac{\Delta y}{\Delta x}$ folgt: \begin{align} m &= \frac{-1 - 2}{3 - 0} \\ m &= - 1 \end{align} Und mit $P \left( 0 \mid 2 \right)$ folgt für $b$: \begin{align} 2 &= -1 \cdot 0 + b \\ b &= 2 \end{align} Also ergibt sich als Funktionsgleichung: $$ y = - x + 2 $$
Gegeben sind die Steigung $m_1$ und der Punkt $P_1 (x_1/ y_1)$.
In der Normalform lautet die Funktionsgleichung
$$
y = m \cdot x + b
$$
Mit den gegebenen Daten lautet die Gleichung
\begin{align}
y_1 &= m_1 \cdot x_1 + b \\
b &= y_1 - m_1 \cdot x_1
\end{align}
Wird der Ausdruck für $b$ in die allgemeine Form eingesetzt, ergibt sich durch Umformung
\begin{align}
y &= m \cdot x + y_1 - m_1 \cdot x_1 \\
&\Downarrow \\
y - y_1 &= m \cdot \left( x - x_1 \right)
\end{align}
Mit dieser Punkt-Steigungs-Form kann die Funktionsgleichung relativ einfach ermittelt werden. Wie oben schon erwähnt, stellen $x$ und $y$
die allgemeinen Variablen dar, die auch in der Funktionsgleichung auftauchen. $x_1$ und $y_1$ sind die Koordinaten eines Punktes $P_1$, der
offensichtlich bekannt ist, oder der aus anderen Angaben ermittelt werden kann.
Bei der Ermittlung der Punkt-Steigungs-Form macht man sich zunutze, dass die Steigung $m$ immer dieselbe ist: $m = m_1$.
Mit dem gleichen Argument kann man für die Steigung also schreiben:
$$
m = \frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}
$$
Das erste Gleichheitszeichen folgt aus der Punkt-Steigungs-Form, das zweite aus der allgemeinen Ermittlung der Steigung durch das Steigungsdreieck.
So erhält man die Zwei-Punkte-Form:
$$
\frac{y - y_1}{x - x_1} = \frac{y_2 - y_1}{x_2 - x_1}
$$
© mondbrand MMXIX