Der waagerechte Wurf

Die wesentliche Grundlage für die Möglichkeit, solche Probleme wie den waagerechten Wurf bearbeiten zu können, ist die Erkenntnis, dass sich Bewegungen unabhängig voneinander überlagern können. Das wird durch das nachfolgende Video demonstriert:

Die unabhängige Überlagerung bedeutet, dass jede beliebige Bewegung als zwei Bewegungen in eine x-Richtung und in eine y-Richtung aufgefasst werden kann.
Um das tun zu können muss zunächst ein Koordinatensystem vorgegeben werden, wobei der Ursprung frei wählbar ist. Allerdings gibt es natürlich sinnvolle Möglichkeiten für die Wahl des Ursprungs und weniger sinnvolle. Die Folge von weniger sinnvollen Positionen ist aber nur, dass es etwas mehr Rechenaufwand bedarf um zu Lösungen zu kommen.

Beispiele für einen waagerechten Wurf

Eine solche Bewegung wird durchgeführt, wenn sich ein Körper mit einer konstanten horizontalen Geschwindigkeit im Schwerefeld der Erde bewegt. Das ist z.B. der Fall, wenn ein Objekt von einer Tischoberfläche gestoßen wird, wenn ein Wasserstrahl aus einem waagerecht gehaltenen Schlauch austritt oder wenn etwas aus einem fliegenden Flugzeug fallen gelassen wird.

Analyse der Bewegungen

Zunächst zur Bewegung in x-Richtung (waagerecht):

Hierbei handelt es sich um eine gleichförmige Bewegung, da der Körper sich mit einer konstanten Geschwindigkeit in x-Richtung bewegt und keine weiteren Kräfte in dieser Richtung auf ihn einwirken. Es gilt also: \begin{align} s_x &= v_x \cdot t \\ v_x &= v_0 \\ a_x &= 0 \end{align}

Zur Bewegung in y-Richtung (senkrecht):

Die Bewegung in y-Richtung ist eine Bewegung mit einer konstanten Beschleunigung, der Fallbeschleunigung. Es gelten die Gesetze des freien Falls: \begin{align} s_y &= - \frac{1}{2} \cdot a_y \cdot t^2 \\ v_y &= - \, a_y \cdot t \\ a_y &= g \end{align} Woher kommen die Minuszeichen? Die kommen daher, weil ein sinnvolles Koordinatensystem seinen Ursprung in der Abwurfstelle hat. Die Bewegung nach unten, also die konstant beschleunigte Bewegung, erfolgt in die negative y-Richtung, da ein kartesisches Koordinatensystem immer so aufgebaut ist, dass die y-Achse nach oben weist, wenn die x-Achse nach rechts zeigt.

Skizze

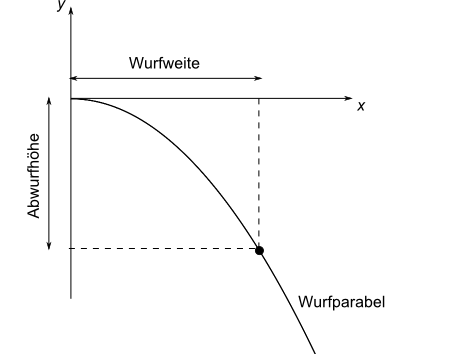
Für die Wurfweite gilt: $s_x = v_0 \cdot t$ und für die Abwurfhöhe: $s_y = - \frac 12 \cdot g \cdot t^2$

Aufstellen der Parabelgleichung

Setzt man $s_x = x$ und $s_y = y$ folgt: \begin{align} x &= v_0 \cdot t \\ t &= \frac{x}{v_0} \\ \\ y &= - \frac 12 \cdot g \cdot t^2 \\ y &= - \frac 12 \cdot g \cdot \left( \frac{x}{v_0} \right)^2 \\ y &= - \frac 12 \cdot \frac{g}{v_0^2} \cdot x^2 \end{align}

Beispielaufgabe

Anatoly Timoschtschuk, ehemaliger Spieler des FC Bayern München, hat am 14.Mai 2011 mit 134,3 km/h eine Rekord-Schussgeschwindigkeit im Fussball erreicht (Quelle). Angenommen, er schafft das noch einmal und schießt einen am Rande einer 10 m hohen Klippe liegenden Ball waagerecht mit eben derselben Geschwindigkeit nach vorn.
Berechne die Stelle, an der der Ball den Boden berührt. Bestimme die Flugzeit des Balls. Gib an, unter welchem Winkel der Ball auf dem Boden aufkommt.

Zunächst muss die Geschwindigkeit in die richtige Einheit umgerechnet werden: $$ 134 \frac{\text{km}}{\text{h}} = \frac{134}{3,6} \frac{\text{m}}{\text{s}} = 37,22 \frac{\text{m}}{\text{s}} $$ Es gilt: \begin{align} y &= - \frac 12 \cdot g \cdot t^2 \\ t &= \sqrt{\frac{2 y}{g}} \\ t &= \sqrt{\frac{2 \cdot 10 \text{ m}}{9,81 \frac{\text{m}}{\text{s}^2}}} \\ t &= 1,428 \text{ s} \end{align} Berücksichtigt wurde hier u.a., dass die Höhe der Klippe über dem Boden gleich der Tiefe des Bodens unter der Klippe ist. Damit ist $y = - 10 \text{ m}$. Weiterhin wurde die zweite Lösung für die Quadratwurzel, hier die negative, vernachlässigt, da sie physikalisch sinnlos ist.
Mit der jetzt bekannten Zeit lässt sich die Schussweite bestimmen: \begin{align} x &= v_0 \cdot t \\ x &= 37,22 \frac{\text{m}}{\text{s}} \cdot 1,428 \text{ s} \\ x &= 53,15 \text{ m} \end{align} Der Auftreffwinkel lässt sich mit Hilfe der Parabelgleichung bestimmen: \begin{align} y &= - \frac 12 \cdot \frac{g}{v_0^2} \cdot x^2 \\ y &= - \frac 12 \cdot \frac{9,81 \frac{\text{m}}{\text{s}^2}}{\left( 37,22 \frac{\text{m}}{\text{s}} \right)^2} \cdot x^2 \\ y &= -0,00354 \text{ m}^{-1} \cdot x^2 \end{align} Der Winkel ergibt sich aus der Steigung der Parabel an der Stelle $x = 53,15 \text{ m}$. Es folgt: \begin{align} m &= \frac{dy}{dx} = - 0,00708 \text{ m}^{-1} \cdot x = - 0,00708 \text{ m}^{-1} \cdot 53,15 \text{ m} \\ m &= - 0,3763 \\ \\ \alpha &= arctan (- 0,3763) \\ \alpha &= - 20,62° \end{align} Der Auftreffwinkel beträgt also 20,62° bei einer Entfernung von 53,15 m von der Klippe. Die Flugzeit beträgt 1,43 s.