

Zunächst wurde das Doppelspaltexperiment 1802 von Thomas Young durchgeführt. Das Ziel war die Bestätigung des Wellencharakters von Licht. Durch die Interferenzphänomene, die durch den Durchgang monochromatischen Lichts durch zwei schmale und dicht beieinanderliegende Spalte entstehen, konnte Licht als Welle identifiziert werden. Der Streit zwischen der Wellentheorie und der Korpuskeltheorie, die von Newton und seit dem immer wieder thematisiert wurde, schien mit dem Doppelspaltexperiment endgültig entschieden zu sein.
Der typische Aufbau des Doppelspaltexperiments ist seitdem im wesentlichen unverändert geblieben.
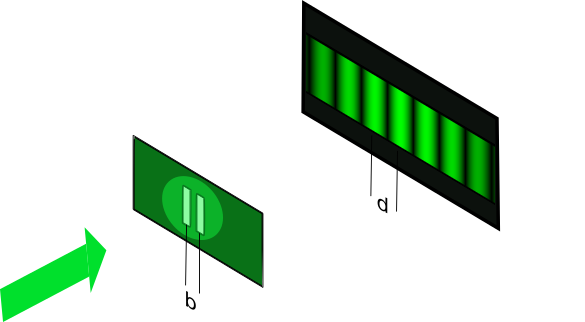
Ein Doppelspalt, zwei schmale und dicht beieinander liegende Spalte werden mit monochromatischem Licht bestrahlt. Auf einem Schirm in
einiger Entfernung wird ein sogenanntes Interferenzmuster erkennbar. Dieses besteht aus hellen und dunklen Bereichen, wobei in der Mitte, also
genau in der Flucht der Mitte zwischen den Spalten ein zentraler heller Bereich beobachtet werden kann. Dieser Bereich wird als nulltes Maximum
bezeichnet. Neben dem nullten Maximum befindet sich das erste Minimum, ein Bereich, in dem kein Licht detektiert werden kann. In einem bestimmten
Abstand folgt ein erstes Maximum, dem ein zweites Minimum folgt, usw.
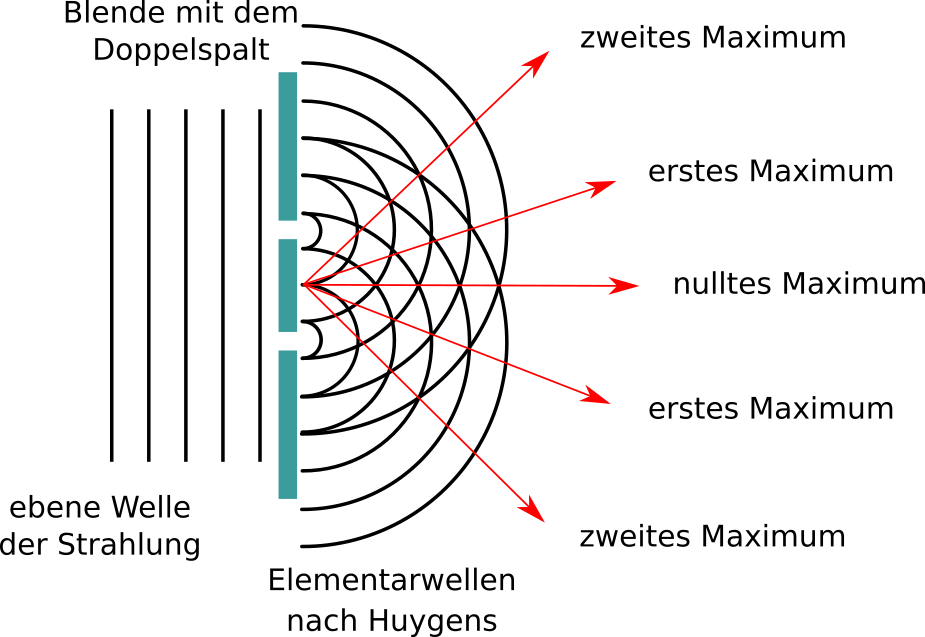
Die Lichtwelle, die an dem Doppelspalt ankommt, kommt näherungsweise als ebene Welle dort an. Hinter den Spalten entstehen nach dem Prinzip
von Huygens zwei Elementarwellen, die sich im weiteren Verlauf überlagern. Da sie aus derselben ebenen Welle entstanden sind, besitzen die beiden
Elementarwellen dieselbe Frequenz und sie bewegen sich in dieselbe Richtung, also wird die Überlagerung als Interferenz bezeichnet. Als Maximum
auf dem Schirm werden nun die Bereiche bezeichnet, an denen die beiden Elementarwellen konstruktiv interferieren. Die Minima sind dann die Bereiche
der destruktiven Interferenz.
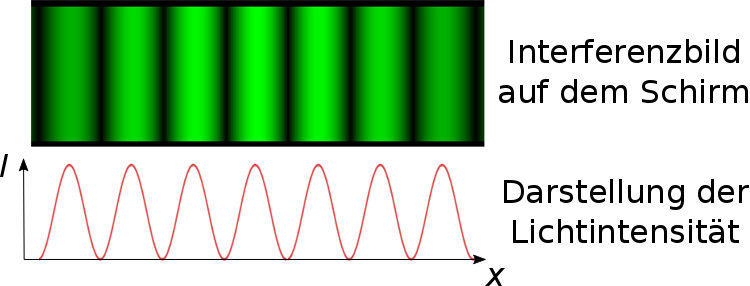
Diese Abfolge von Minima und Maxima lässt sich auch durch die folgende Darstellung illustrieren:
Die Auswertung erfolgt zunächst mit ein wenig Geometrie. Mit $b$ wird der Abstand der beiden Spalte bezeichnet, $d$ bezeichnet den Abstand des
ersten vom nullten Maximum. $l$ ist der Abstand des Schirms vom Doppelspalt.
Der Abstand $l$ ist dabei sehr viel größer als der Spaltabstand $b$. Es gilt: $l \gg b$
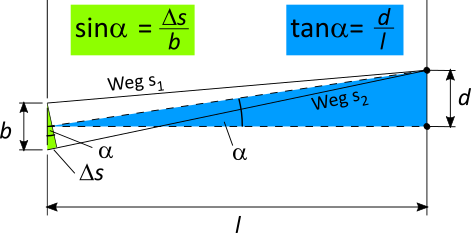
Die Lichtwelle, die durch den oberen Spalt an der Position des ersten Maximums auf den Schirm trifft, legt den Weg $s_1$ zurück. Die Welle, die
durch den unteren Spalt an derselben Stelle auf den Schirm trifft, legt den Weg $s_2$ zurück.
Die Länge der beiden Wege unterscheiden sich um den Betrag $\Delta s$. Damit auf dem Schirm eine konstruktive Interferenz auftritt, muss der Wegunterschied ein ganzzahliges Vielfaches der Wellenlänge des Lichts sein. Die Bedingung für konstruktive Interferenz lautet: $$ \Delta s = n \cdot \lambda $$ Wegen $l \gg b$ gilt weiterhin, dass die beiden mit $\alpha$ bezeichneten Winkel ungefähr gleich groß sind. Das ist die sogenannte Kleinwinkelnäherung. Damit gilt auch: $\sin \alpha \approx \tan \alpha$ und folglich: $$\frac{\Delta s}{b} = \frac{d}{l}$$ $$\frac{n \cdot \lambda}{b} = \frac{d}{l}$$ $$\lambda = \frac{b \cdot d}{l}$$ wenn n = 1 ist, es sich also um das erste Maximum handelt.
Für die Minima muss für $\Delta s$ gelten: $$ \Delta s = \left( n - \frac12 \right) \cdot \lambda $$ Der Wegunterschied der beiden Elementarwellen muss einem ungeradzahligen Vielfachen der halben Wellenlänge entsprechen (also etwa $\frac12 \lambda$, $\frac32 \lambda$, $\frac52 \lambda$, ...). Damit ergibt sich für das erste Minimum: $$\frac{\Delta s}{b} = \frac{d}{l}$$ $$\frac{\left(n-\frac12 \right) \cdot \lambda}{b} = \frac{d}{l}$$ $$\lambda = 2 \cdot \frac{b \cdot d}{l}$$
© mondbrand MMXIX