Jede physikalische Arbeit $W$ ist die Veränderung der Energie eines Systems. Wenn ein System also eine bestimmte Energie hat, kann es durch Abgabe dieser Energie Arbeit verrichten. Andererseits ist es möglich, durch Arbeit an einem System diesem Energie zuzuführen.
Ein Beispiel dafür sind die Pumpspeicherkraftwerke.
Mit Hilfe nicht benötigter elektrischer Energie wird Wasser in ein höher gelegenes
Reservoir gepumpt und dort gespeichert (Stausee). Wird die elektrische Energie benötigt, kann man das Wasser in einer kontrollierten Menge
wieder aus dem Reservoir herausfließen lassen. Dadurch wird eine Turbine bewegt, die durch einen Generator elektrische Energie erzeugt.
Links ist eine Stausee-Anlage in Österreich zu sehen (Quelle).
Arbeit bedeutet also Veränderung von Energie. $$ W = \Delta E $$
Arbeit ist meist auf mechanische Energieübertragungen beschränkt. Wärmekraftmaschinen etwa übertragen Energie durch die
Wärme $Q$.
Das durch den Begriff "Wärmekraft" natürlich auf eine mechanische Wirkung, nämlich die der Kraft hingewiesen wird, macht die
Angelegenheit manchmal etwas unübersichtlich. Hier bleibt festzuhalten:
Arbeit $W$ und Wärme $Q$ sind Möglichkeiten, den Energieinhalt eines Systems zu verändern.
Die Einheit der Arbeit und auch der Wärme ist dabei wie die Einheit der Energie das Joule. \begin{align} \text{Arbeit} \; W \qquad &[W]=1 \; \text{J} \\ \text{Wärme} \; Q \qquad &[Q]=1 \; \text{J} \\ \text{Energie} \; E \qquad &[E]=1 \; \text{J} \end{align}
Arbeit ist das Produkt aus Kraft und Weg. Wenn eine Kraft $F$ auf einen Körper der Masse $m$ ausgeübt wird, wird der Körper
anfangen sich zu bewegen. Je länger die Kraft entlang des Weges einwirkt, umso schneller wird der Körper werden. Der Körper wird auch
dann schneller, wenn die Kraft größer wird. Insgesamt ergibt sich für den einfachsten Fall, das die Kraft und der Weg in dieselbe
Richtung zeigen, folgendes:
$$
E = F \cdot s
$$
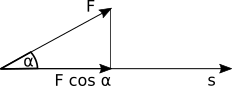Im Allgemeinen sind Kraft und Weg aber nicht parallel zueinander, sondern es gibt einen Winkel zwischen den Richtungen. Dann muss der Anteil
der Kraft, der parallel zum Weg verläuft, bestimmt werden. Nach der Skizze ist das der Term $F \cdot \cos \alpha$. Für die Energie
erhält man damit:
$$
E = F \cdot s \cdot \cos \alpha
$$
Wenn man etwas anheben möchte, muss man mindestens die Gewichtskraft des anzuhebenen Körpers aufbringen. Wenn die Kraft größer als die Gewichtskraft ist, gibt es eine resultierende Kraft in Heberichtung, und die Hebebewegung ist eine beschleunigte Bewegung. Sind beide Kräfte allerdings gleich groß, befindet sich der anzuhebene Körper im Gleichgewicht. Da nun aber keine resultierende Kraft in Heberichtung auftritt, dauert das Anheben um einen beliebigen Weg unendlich lange.
Das ist aber kein Problem, da in den idealisierten Fällen, die am Ende zu den Formeln führen, erstens die Zeit keine Rolle spielt und zweitens jeder Prozess so abläuft, dass die Körper zu jedem Zeitpunkt im Gleichgewicht sind.
Für die Hubarbeit eines vollen Kaffeebechers mit $m = 670 \text{ g}$ um $h = 0,3 \text{ m}$ etwa ergibt sich die folgende Rechnung: \begin{align} W_{Hub} &= F_G \cdot h \\ &= m \cdot g \cdot h \\ &= 0,67 \text{ kg} \cdot 9,81 \, \frac{\text{m}}{\text{s}^2} \cdot 0,3 \text{ m} \\ &= 1,97 \text{ J} \end{align}
Durch die geleistete Hubarbeit wurde dem Becher die Energie $E = 1,97 \text{ J}$ hinzugefügt. Die Energie des Bechers wird potentielle Energie genannt.
Die potentielle Energie eines Körpers ist die Energie, die der Körper aufgrund seiner Höhe über einer Bezugsebene hat. Andere Begriffe sind Höhenenergie oder Lageenergie.
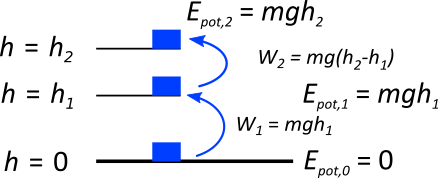Die potentielle Energie des Körpers auf der Bezugsebene ist dann immer $E_{pot} = 0$. Merke: Die geleistete Hubarbeit führt dazu,
dass sich die potentielle Energie erhöht und nicht, dass sie der geleisteten Arbeit entspricht.
$$E_{pot,1} = E_{pot,0} + W_1$$
$$E_{pot,2} = E_{pot,1} + W_2$$
Wenn der Becher nun diese Energie bekommen hat, wird er, sofern er nicht daran gehindert wird, diese Energie wieder abgeben wollen. Das passiert am einfachsten, indem er der Erdanziehung folgt und herunterfällt.
Für den freien Fall gelten die Zusammenhänge: \begin{align} s = \frac{1}{2} \cdot g \cdot t^2 \\ v = g \cdot t \end{align} mit der Beschleunigung $g = 9,81 \frac{\text{ m}}{\text{ s}^2}$.
Eingesetzt in die Formel für die potentielle Energie ergibt sich: \begin{align} E = m \cdot g \cdot h \\ E = m \cdot g \cdot \frac{1}{2} \cdot g \cdot t^2 \\ E = \frac{1}{2} \cdot m \cdot g^2 \cdot t^2 \\ E = \frac{1}{2} \cdot m \cdot v^2 \end{align} Die Fallhöhe $h$ ist dabei der zurückgelegte Weg $s$.
In der Energieformel taucht neben der Masse $m$ die Geschwindigkeit $v$ auf. Die Energie ist also die kinetische Energie oder Bewegungsenergie, die ein Maß für den Energiebetrag aufgrund der Bewegung darstellt.
Dasselbe Ergebnis erhält man, wenn man von $E = F \cdot s$ und $F = m \cdot a$ ausgeht und dabei die Bewegungsgleichungen $s = \frac{1}{2} a t^2$ sowie $ v = a t$ einsetzt.
Dabei wird berücksichtigt, dass dem System keine weitere Energie zugeführt wird, dass also keine weitere Arbeit an ihm geleistet wird. Die Gesamtenergie des Systems bleibt konstant, die gesamte potentielle Energie wird komplett in die kinetische Energie überführt.
Wenn einem System keine Energie zugeführt wird und wenn ein System auch keine Energie abgibt, nennt man das System energetisch abgeschlossen. In einem abgeschlossenen System bleibt die Gesamtenergie, also die Summe der einzelnen Energieformen, konstant. Es gilt: $$ \Sigma E = \text{konstant} $$
In dem Beispiel gilt also, dass die Summe der potentiellen und der kinetischen Energie vor dem Fall genau so groß ist wie die Summe der potentiellen und kinetischen Energie zu jedem Zeitpunkt des Falls, z.B. auch genau zum Zeitpunkt des Aufpralls. $$ E_{pot,vor} + E_{kin,vor} = E_{pot, Aufprall} + E_{kin,Aufprall} $$ Der Zeitpunkt des Aufpralls ist nicht der Zeitpunkt nach dem Fall. Vor dem Fall ist die potentielle Energie maximal und die kinetische Energie ist Null, d.h. die Gesamtenergie ist gleich der potentiellen Energie. Die Gesamtenergie bleibt konstant. Also ist beim Aufprall die Gesamtenergie gleich der Summe der potentiellen und der kinetischen Energie. Die potentielle Energie beim Aufprall ist aber Null (Aufprall = Höhe Null), also ist die kinetische Energie gleich der Gesamtenergie.
Nach dem Fall ist sowohl die potentielle als auch die kinetische Energie Null. Das System hat also Energie abgegeben (= der Becher ist kaputt). \begin{align} E = \frac{1}{2} m v^2 \\ v = \sqrt{\frac{2E}{m}} \\ v = \sqrt{\frac{2 \cdot 1,97 \text{ J}}{0,67 \text{ kg}}} \\ v = 2,425 \, \frac{\text{m}}{\text{s}} \end{align} Der Becher kommt also mit einer Geschwindigkeit von $2,425 \, \frac{\text{m}}{\text{s}} = 8,73 \, \frac{\text{km}}{\text{h}}$ auf dem Boden auf.
Die dritte mechanische Energieform ist die Energie, die in einer elastischen Verformung steckt. Die Benennung ist unterschiedlich; mal wird sie als Federenergie, mal als Spannenergie oder auch als elastische Energie bezeichnet. Hier soll der Begriff elastische Energie genutzt werden.
Sie wird im Falle einer gespannten Feder bestimmt, indem der Zusammenhang zwischen Kraft und Weg genutzt wird: $$ E = F \cdot s $$ Eine der Haupteigenschaften einer Feder ist, dass der Kraftaufwand, die Feder auseinanderzuziehen, mit zunehmender Länge der Feder auch zunimmt. Die Kraft $F$ ist also abhängig von der Federverlängerung: $F(s)$.
Mit der Annahme, dass die Kraft von Null bis zum Maximum der Kraft linear zunimmt, gilt:
$$
\overline{F} = \frac{1}{2} \cdot F_{max}
$$
Hier ist $\overline{F}$ der durchschnittliche und damit der als konstant anzunehmende Betrag der Kraft. Mit dem Zusammenhang $F = D \cdot s$ aus
der Federkraft folgt:
$$
E = \overline{F} \cdot s \\
E = \frac{1}{2} \cdot F_{max} \cdot s \\
E = \frac{1}{2} \cdot D \cdot s^2
$$
Dabei ist $D$ die Federkonstante des elastischen Systems und $s$ die Größe der Verformung. (zur Federkraft)
In der Praxis tritt Reibarbeit immer dann auf, wenn sich zwei Körper relativ zueinander bewegen. Damit verbunden ist die Umwandlung von kinetischer Energie in Wärme (Energieentwertung). Reibung bewirkt immer, dass dem System Energie entzogen wird.
Mit dem allgemeinen Zusammenhang $E = F \cdot s$ kann man die Reibarbeit bestimmen, wenn die Reibkraft $F_R$ bekannt ist. (zur Reibkraft)
Bei der Rotation eines Körpers handelt es sich um eine Drehbewegung um ein Drehzentrum, dass nicht unbedingt innerhalb des Körpers liegen muss. Aus diesem Grund wird die Rotationsenergie auch kinetische Energie der Rotation genannt, d.h. es handelt sich um eine Form der Bewegungsenergie. Die bisher betrachtete Form der Bewegungsenergie wird somit zur kinetischen Energie der Translation, d.h. der geradlinigen Bewegung.
© mondbrand MMXIX