

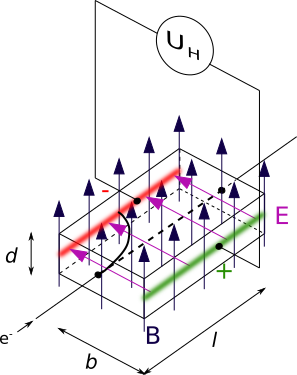
Die Abbildung umfasst bereits alle wesentlichen Elemente, die bei der Beschreibung des Hall-Effekts eine Rolle spielen werden.
Zunächst betrachtet man einen Block aus leitfähigem Material. Dieser Block hat die Abmessungen Länge $l$, Breite $b$ und Dicke $d$. Durch eine Leitung treten von vorne Elektronen in den Block ein und hinten wieder aus. Die Elektronen werden sich nahezu geradlinig durch den Block bewegen (gestrichelte Linie).
Nun wird der gesamte Block mit einem nach oben gerichteten Magnetfeld $B$ durchsetzt. In der Abbildung sind das die dunkelblauen Pfeile. Die sich bewegenden Elektronen, die gerade in den Block und damit auch in das Magnetfeld eintreten, erfahren eine Lorentzkraft, die sie zwingt, ihre Bewegungsrichtung zu verändern. Mit der Linke-Hand-Regel kann man nachprüfen, dass die Elektronen sich nach links ablenken lassen.
(Linke-Hand-Regel: Der Daumen weist in die Bewegungsrichtung der Elektronen, der Zeigefinger zeigt die Magnetfeldrichtung an und der Mittelfinger zeigt in die Wirkungsrichtung der Lorentzkraft.)
Mit der Zeit wandern alle in das Magnetfeld eintretenden Elektronen nach links und sammeln sich auf dieser Seite des Blocks. Es bildet sich ein Elektronenüberschuss und damit negative Ladung auf der linken Seite. In der Abbildung wird das durch den roten Streifen angedeutet. In Folge dessen wird die rechte Seite als positiv geladen betrachtet (Positiv im Vergleich zu der linken Seite!), angedeutet durch den grünen Streifen. Die beiden Seiten können nun als die beiden Platten eines Plattenkondensators betrachtet werden. Zwischen diesen bildet sich ein elektrisches Feld $E$ aus, was in der Abbildung durch die violetten Pfeile zu sehen ist.
Beide Felder, das magnetische B-Feld und das elektrische E-Feld üben eine Kraft auf die Elektronen aus. Das B-Feld treibt die Elektronen nach links und das E-Feld treibt sie nach rechts. Solange das B-Feld stärker ist als das E-Feld, werden die Elektronen nach links wandern. Der Radius der Kreisbewegung der Elektronen wird dabei immer größer, die Elektronen treffen immer später auf die linke Seite des Blocks auf. Sobald die beiden Kräfte gleichgroß sind, bewegen sich die Elektronen wieder geradlinig durch den Block. Es hat sich ein dynamisches Gleichgewicht zwischen den beiden Kräften eingestellt. Von der linken Seite werden immer wieder Elektronen den Block verlassen können, worauf das E-Feld schwächer wird. Aufgrund des jetzt wieder stärkeren B-Feldes werden die nächsten Elektronen wieder nach links abgelenkt und stellen somit das Gleichgewicht wieder her.
Den Ladungsunterschied zwischen der linken und der rechten Seite kann durch die Messung der sogenannten Hall-Spannung $U_{H}$ bestimmt werden. Aus der Definition der Spannung in einer Plattenkondensatoranordnung, $U = E \cdot b$, folgt die Kenntnis der elektrischen Feldstärke, die zum Kräftegleichgewicht führt.
Die Hall-Spannung wird erst im Gleichgewicht bestimmt, d.h., wenn die Elektronen sich geradlinig durch den Block bewegen. Dieses Gleichgewicht besteht zwischen der elektrischen Kraft $F_E$ und der Lorentzkraft $F_L$. Also: \begin{align} F_E &= F_L \\ e \cdot E &= e \cdot v \cdot B \\ E &= v \cdot B \end{align} Mit $E = \frac{U}{b}$ folgt: \begin{align} U &= b \cdot v \cdot B \\ U_H &= b \cdot v \cdot B \end{align} Die Geschwindigkeit $v$ der Elektronen ist hier nicht ohne Weiteres zu bestimmen. Sie hängt neben der Stromstärke u.a. von der Dichte der Ladungsträger in dem verwendeten Material ab.
Die Ladungsträgerdichte $n$ ist die Anzahl der Ladungsträger $N$ pro Volumen $V$. Es gilt: \begin{align} n &= \frac{N}{V} \\ n &= \frac{N}{b \cdot l \cdot d} \end{align} Nimmt man eine mittlere Geschwindigkeit der Elektronen (Ladungsträger) $v = \frac{l}{t}$ an, mit $l$ als der in der Zeit $t$ zurückgelegte Weg $s$ einer gleichförmigen Bewegung, folgt für die Stromstärke: \begin{align} I &= \frac{Q}{t} \\ I &= \frac{N \cdot e}{t} \\ I &= N \cdot e \cdot \frac{v}{l} \end{align} Damit erhält man für die Geschwindigkeit $v$ den Ausdruck \begin{align} v &= \frac{I \cdot l}{N \cdot e} \end{align} Mit $N = n \cdot b \cdot l \cdot d$ folgt \begin{align} v &= \frac{I}{ n \cdot b \cdot d \cdot e} \end{align} Wird die Geschwindigkeit nun in die Gleichung für die Hall-Spannung eingesetzt, erhält man \begin{align} U_H &= \frac{I \cdot B}{n \cdot e \cdot d} \\ \\ U_H &= \frac{1}{n \cdot e} \cdot \frac{I}{d} \cdot B \end{align} Der Faktor $\frac{1}{n \cdot e}$ wird als Hall-Konstante $R_H$ bezeichnet. Also: \begin{align} U_H = R_H \cdot \frac{I}{d} \cdot B \end{align} mit $R_H = \frac{1}{n \cdot e}$.
© mondbrand MMXIX