Der sogenannte äußere photoelektrische Effekt wurde erstmals 1839 von Alexandre Becquerel beobachtet. Er stellte die Freisetzung von Ladungsträgern aus einer in einem Elektrolyten befindlichen blanken Metalloberfläche fest, wenn sie mit Licht bestrahlt wird. Dieser Effekt wurde demzufolge auch Becquerel-Effekt genannt.
Heinrich Hertz beobachtete 1886 den Einfluss von UV-Strahlung auf die Metalloberflächen einer Funkenstrecke. Dabei äußert sich die UV-Strahlung in einer Verlängerung der Funken. Wird die UV-Strahlung dagegen abgeschirmt, verkürzen sich die Funken. Für diesen Effekt gab es die Erklärung, dass durch die UV-Strahlung aus den Elektroden Elektronen freigesetzt werden, die im Anschluss bei einer deutlich kleineren Feldstärke die Funkenstrecke bilden, da sie nicht erst aus dem Metall heraustreten müssen.
Hertz' damaliger Assistent, Wilhelm Hallwachs, führte systematische Untersuchungen zu diesem Effekt durch, wodurch die Bezeichnung Hallwachs-Effekt gebräuchlich wurde. Er stellte u.a. fest, dass sich eine Metallplatte elektrisch aufladen lässt, wenn man sie mit einer Lichtbogenlampe bestrahlt.
Im Jahre 1899 konnte Phillip Lenard durch Experimente im Hochvakuum feststellen, dass es sich bei den durch den Photoeffekt freigesetzten Ladungsträgern um Elektronen handelt. Er maß die spezifische Ladung der Ladungsträger durch ihre Ablenkung in einem Magnetfeld. Weiterhin konnte er die Abhängigkeit des Effekts von der Frequenz und der Bestrahlungsstärke feststellen.
Albert Einstein konnte 1905 in seiner Arbeit „ Ueber einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt“ die korrekte Erklärung des Effekts liefern. Er erhielt dafür 1921 den Nobelpreis für Physik.
Robert Millikan konnte zwischen 1912 und 1915 mit der Gegenfeldmethode die übereinstimmung des Proportionalitätsfaktors in der Einstein-Gleichung mit dem Planck'schen Wirkungsquantum $h$ feststellen: $$E_{kin} = h \cdot f - E_A$$
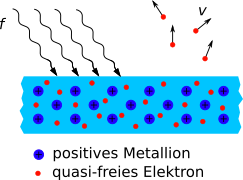Licht strahlt mit einer Frequenz $f$ bzw. einer Energie $hf$ auf eine Metalloberfläche. Die Energie des Lichts wird von den quasi-freien Elektronen des
Metalls aufgenommen. Wenn die Energie der Elektronen ausreicht, d.h. mindestens so groß ist wie die Austrittsarbeit des Metalls, können sie das
Metall verlassen und sich dann frei mit einer Geschwindgkeit $v$, d.h. mit der kinetischen Energie $E_{kin}$ bewegen.
Die Energie des Lichts wird somit in Austrittsarbeit und Bewegungsenergie der Elektronen umgewandelt.
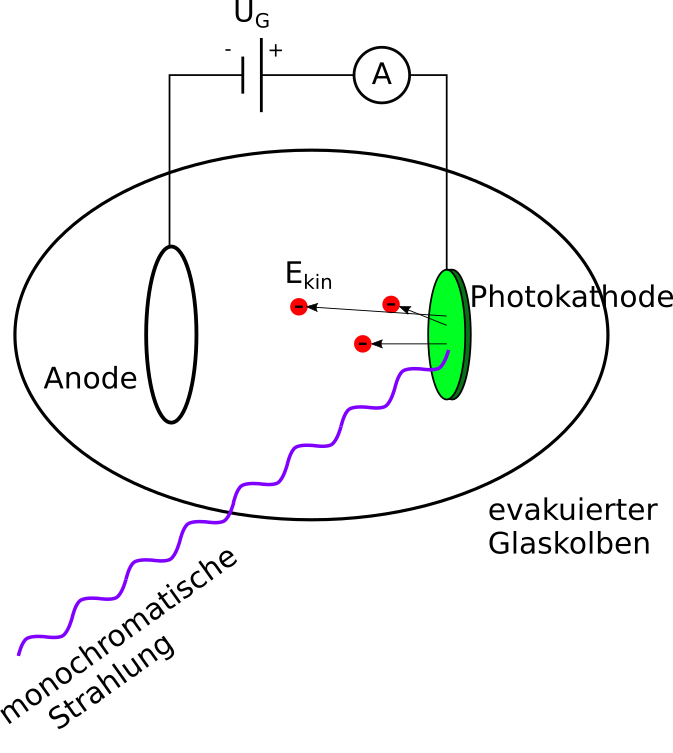
Die Gegenfeld-Methode wurde von Millikan verwendet, um den Photoeffekt zu vermessen. Bei der Methode wird eine Metall-Kathode (auch Photokathode)
mit monochromatischem Licht bestrahlt. Durch
den Photoeffekt treten Elektronen aus der Metalloberfläche aus, die sich aufgrund ihrer kinetischen Energie u.a. in Richtung einer Anode bewegen.
Der so entstehende Stromfluss wird durch ein empfindliches Ampèremeter gemessen.
Zwischen der Kathode und der Anode wird nun eine Spannung angelegt, die dem Stromfluss entgegengerichtet ist, d.h. die Kathode wird auf positives Potential gelegt. Dadurch werden die Elektronen abgebremst. Ab einer bestimmten Gegen-Spannung kommen keine Elektronen mehr an der Anode an.
Der Versuch wird mit Licht verschiedener Frequenzen durchgeführt; die entsprechenden Gegenspannungen werden notiert.
Es entsteht z.B. eine solche Tabelle:
| $f$ in $10^{14} \, \text{Hz}$ | 7,5 | 6,7 | 6,0 | 5,5 | 5,0 |
| $U_G$ in $\text{V}$ | 1,25 | 0,90 | 0,62 | 0,40 | 0,17 |
| $f$ in $10^{14} \, \text{Hz}$ | 7,5 | 6,7 | 6,0 | 5,5 | 5,0 |
| $E_{kin}$ in $\text{eV}$ | 1,25 | 0,90 | 0,62 | 0,40 | 0,17 |
Die Werte für $E_{kin}$ werden über $f$ aufgetragen. Verbindet man die Punkte im Koordinatensystem durch eine Gerade, entstehen zwei wichtige
Punkte: der Schnittpunkt mit der $y$-Achse und der Schnittpunkt mit der $x$-Achse.
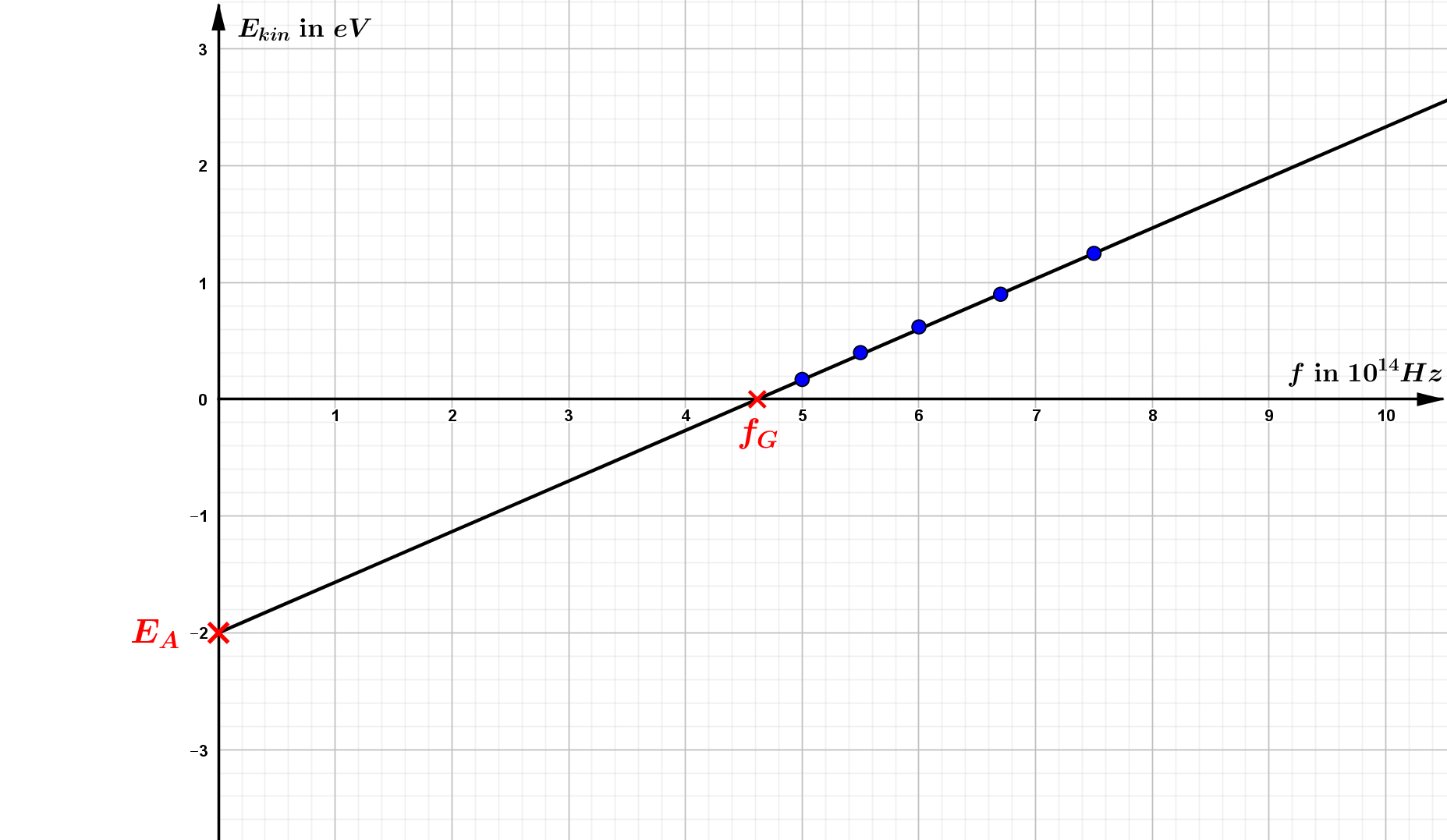
Den Schnittpunkt mit der $x$-Achse kann man so interpretieren, dass bei dieser Frequenz überhaupt erst Elektronen aus der Metalloberfläche emittiert
werden, die dann die kinetische Energie Null haben, sich also nicht bewegen. Diese Frequenz wird Grenzfrequenz $f_G$ genannt.
Die Energie, die die Elektronen aufwenden müssen, um den Metallverband verlassen zu können, wird mit Austrittsarbeit $E_A$, bezeichnet. Diese Energie wird durch den Schnittpunkt mit der $y$-Achse bezeichnet.
Die Gesamtenergie wird durch die Summe der kinetischen Energie der Elektronen und der Austrittsarbeit gebildet und ist gleich der Energie der verwendeten Bestrahlung.
In dem Beispiel ergibt sich eine Grenzfrequenz von $f_G = 4,6 \cdot 10^{14} \, \text{Hz}$ (das entspricht etwa einem rot-orangen Licht) und eine Austrittsarbeit von $E_A = 2 \, \text{eV}$ (möglicherweise Cäsium).
Für die Austrittsarbeit und die Grenzfrequenz gilt der Zusammenhang $$ E_A = h \cdot f_G $$ Interessant ist noch die Steigung der Geraden, die sich aus dem Quotienten der Energiedifferenz und der dazugehörigen Differenz der Frequenzen bestimmt. Dafür muss die Energiedifferenz wieder in der Einheit Joule angegeben werden. Es gilt $1 \, \text{eV} = 1,602 \cdot 10^{-19} \, \text{J}$ $$ \frac{\Delta E}{\Delta f} = \frac{(1,25 - 0,17) \cdot 1,602 \cdot 10^{-19} \, \text{J}}{(7,5 - 5,0) \cdot 10^{14} \, \text{Hz}} = 6,92 \cdot 10^{-34} \, \text{Js} $$ Das entspricht in etwa dem Planckschen Wirkungsquantum $h = 6,626 \cdot 10^{-34} \, \text{Js}$. Die Gerade folgt dem Funktionsterm $$ E_{kin} = h \cdot f - E_A $$ was einer linearen Funktion mit der Steigung $h$ und dem Achsenabschnitt $E_A$ entspricht.
© mondbrand MMXIX