Das Modell des linearen Potentialtopfs

Hintergrund

Der lineare Potentialtopf ist eine Darstellungsform, durch die eine Aussage über den Aufenthaltsort von Elektronen getroffen werden kann. Dabei wird zunächst das Atom insgesamt außen vor gelassen. Für den Potentialtopf gelten bestimmte Randbedingungen, die nicht unbedingt von einem Atom abhängen, sondern auch z.B. für Moleküle oder ähnliche Objekte gelten können, in denen sich Elektronen aufhalten.

Die Bedingungen für den Potentialtopf sind folgende:

Innerhalb des Topfs ist die potentielle Energie der Elektronen Null
Außerhalb des Topfs ist die potentielle Energie unendlich
Der Topf hat eine Länge $L$

Durch die Forderung $E_{pot} = 0$ bewegt sich das Elektron kräftefrei und damit ohne Einfluss einer weiteren Ladung. Das bedeutet, dass für das Modell des linearen Potentialtopfs zunächst kein Atomkern, der eine positive Ladung darstellt, vorhanden ist. Wegen der unendlich hohen potentiellen Energie außerhalb kann sich das Elektron nicht außerhalb des Topfs aufhalten. Es ist somit innerhalb des Topfs gefangen.

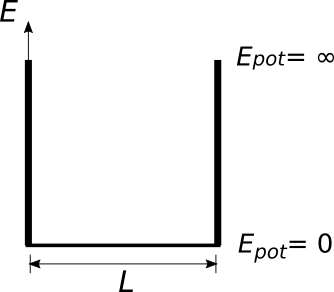
Ein Elektron, das in einem bestimmten Bereich eingesperrt ist, kann durch eine stehende Welle beschrieben werden. Das Quadrat der Wellenamplitude kann dabei als Wahrscheinlichkeit, das Elektron an diesem Ort anzutreffen, gedeutet werden.

Eine stehende Welle entsteht dann, wenn eine Welle an zwei festen Enden reflektiert wird. Dabei gilt, dass es verschiedene Modi der stehenden Welle gibt. Im ersten Modus entspricht die Länge des Bereichs zwischen den Enden genau der halben Wellenlänge $\left( L = \frac{\lambda}{2} \right)$, im zweiten Modus genau einer Wellenlänge $\left( L = \lambda \right)$, im dritten drei halben Wellenlängen $\left( L = \frac{3 \lambda}{2} \right)$, usw. Insgesamt gilt für die Länge des Bereichs also $\left( L = \frac{n \lambda}{2} \right)$.

Energiewerte

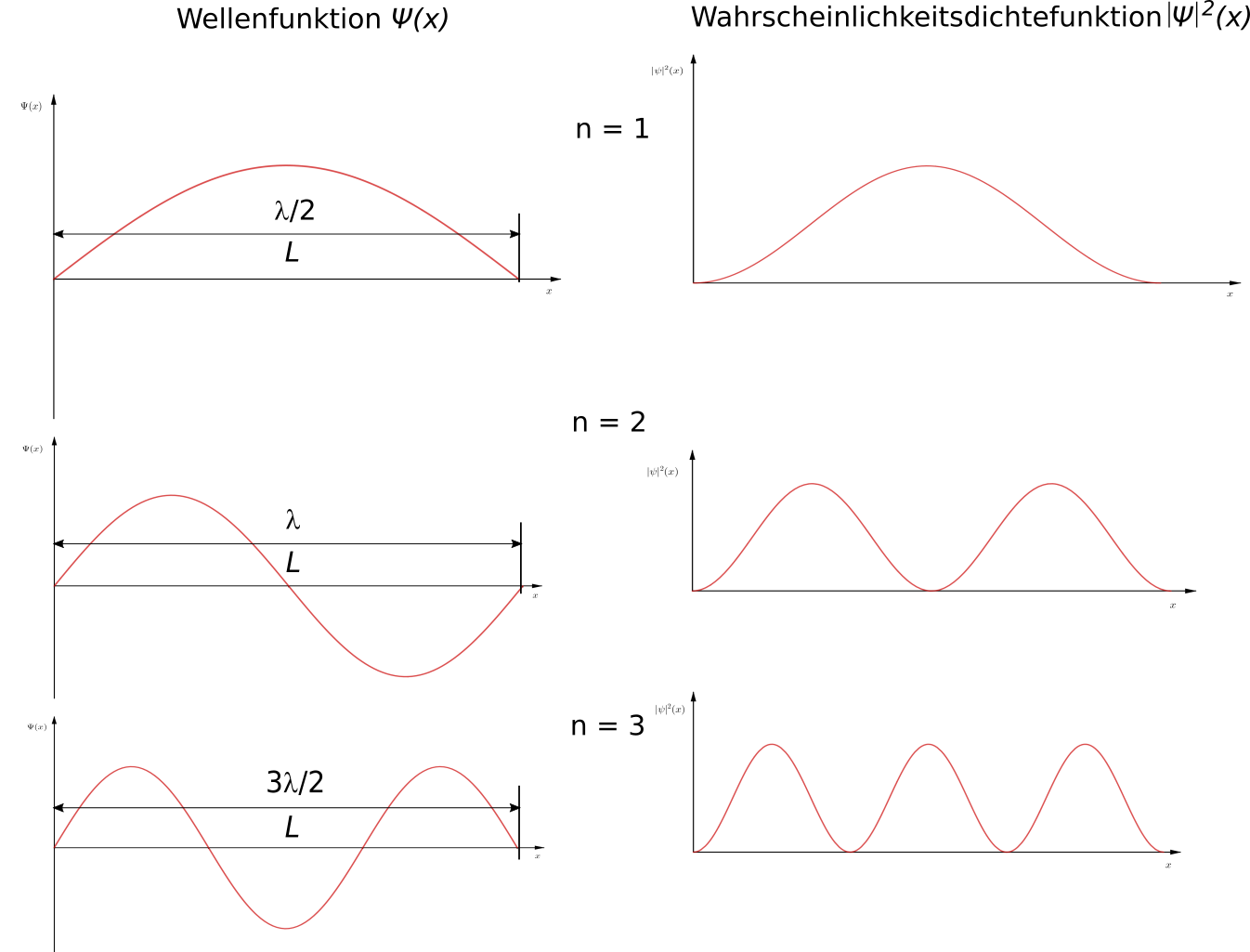
Die gesamte Energie eines Elektrons teilt sich in potentielle und kinetische Energie auf. Da aber innerhalb des Potentialtopfs die potentielle Energie gleich Null gesetzt wurde, entspricht die Energie eines Elektrons im Potentialtopf der kinetischen Energie. Es gilt also: $$ E = E_{kin} = \frac12 mv^2 $$ Mit $p = mv$ führt das zu $$ E = \frac{p^2}{2m} $$ Weiterhin gilt $\lambda = \frac{2L}{n}$ und nach de Broglie $\lambda = \frac{h}{p}$. Damit erhält man $$ \frac{2L}{n} = \frac{h}{p} $$ Umgestellt nach $p$ und in die Energieformel eingesetzt: $$ E = \frac{h^2}{8mL^2} \cdot n^2 $$ Die Energiewerte, die ein Elektron im Potentialtopfmodell annehmen kann, hängen also von $n^2$ ab. Da $n$ aber eine natürliche Zahl ist, bedeutet dies, dass die Energie der Elektronen gequantelt ist. Das ist auch eine der wesentlichen Aussagen aus dem Modell.

Weiterhin hängt die Energie auch von der Länge des Potentialtopfs ab. Es gilt: $E \sim \frac{1}{L^2}$. Wenn der Aufenthaltsbereich für das Elektron kleiner wird, steigt die Energie. Berechnet man die Energie für ein Wasserstoffatom mit $L \approx 10^{-10} \text{ m}$ und $n = 1$, folgt: $$ E = \frac{h^2}{8mL^2} \cdot n^2 \\ \\ E \approx 37,6 \text{ eV} $$ Dieser Wert entspricht nicht dem aus den Ansätzen nach Bohr. Das liegt unter anderem daran, dass es sich um ein Modell mit sehr starker Vereinfachung handelt, es gibt z.B. keine Zentralladung (Atomkern). Allerdings stimmen die Größenordnungen der Energie und auch aus dem Ansatz mit dem Potentiatopf und dem Elektron als stehende Welle innerhalb des Topfs geht hervor, dass die Energieen, die ein Elektron annehmen kann, gequantelt sein müssen.

Erweiterung des Modells

Fügt man in die Darstellung der Wellenfunktion den Atomkern hinzu, folgt für die Wahrscheinlichkeitsdichte für $n = 1$ etwa der folgende Verlauf:

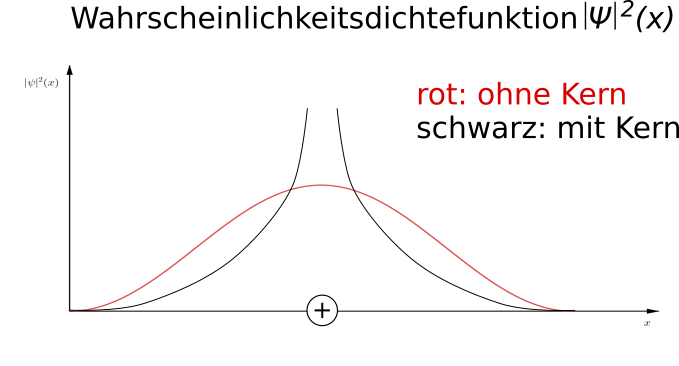
Die Wahrscheinlichkeitsdichte nimmt in Kernnähe sehr stark zu, da das Elektron natürlich vom Kern angezogen wird.

Die Darstellung der Wahrscheinlichkeitsdichte führt zu der tatsächlichen Wahrscheinlichkeit über den folgenden Ansatz:

Unterteilt man das Volumen um den Kern herum in gleichdicke Kugelschalen, entspricht die Wahrscheinlichkeit dem Produkt aus Wahrscheinlichkeitsdichte und dem Volumen der Schale. Für die Wahrscheinlichkeit $w$, in einem Abstand $x$ vom Kern ein Elektron anzutreffen, gilt somit: $$ w(x) = \vert \Psi \vert ^2 (x) \cdot \text{d}V $$ Für die Bereiche in Kernnähe, deren Wahrscheinlichkeitsdichte sehr groß sind, folgt eine kleine Wahrscheinlichkeit, weil das Schalenvolumen sehr klein ist. Bereiche, die weit vom Kern entfernt sind, haben ebenfalls eine kleine Wahrscheinlichkeit, da zwar das Schalenvolumen groß, dafür aber die Wahrscheinlichkeitsdichte sehr klein ist. Für einen bestimmten Abstand vom Kern folgt mit diesem Ansatz ein Maximum der Wahrscheinlichkeit. Dieser Abstand entspricht bei einer entsprechenden Berechnung genau dem Bohrschen Radius.

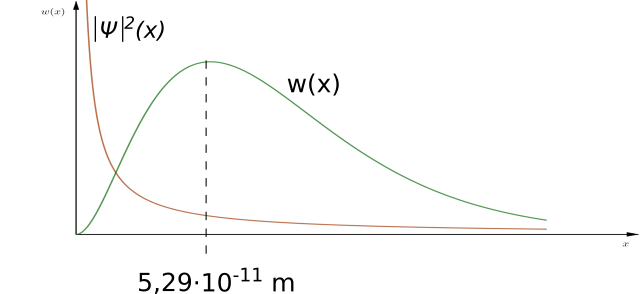
Während sich das Elektron nach dem Bohrschen Atommodell nur genau auf diesem Radius aufhalten kann, ergibt sich im quantenmechanischen Atommodell dieser Radius als der Abstand mit der größten Aufenthaltswahrscheinlichkeit.

Das quantenmechanische Orbitalmodell ist der Versuch, die Wahrscheinlichkeitsdichteverteilung für verschiedene Energieniveaus bildlich darzustellen. Dazu sei hier auf das HydrogenLab verwiesen, welches von der Universität Karlsruhe und dem Karlsruher Physikkurs betrieben wird.