Der schweizer Mathematiker und Physiker Johann Jakob Balmer untersuchte Gasentladungen in Wasserstoff und das dadurch ausgesandte Licht. Er vermutete einen
Zusammenhang zwischen dem Licht und dem Atomaufbau. Das emittierte Licht wurde durch ein Gitter spektral zerlegt und zeigte vier diskrete Linien im
sichtbaren Bereich, das sogenannte Linienspektrum.
Die zu sehenden Linien haben für kleinere Wellenlängen kürzere Abstände vonenander. Balmer kombinierte die Daten geschickt
miteinander und konnte schließlich eine Formel aufstellen, die das Auftreten der Linien reproduzieren konnte. Die sogenannte Balmer-Formel lautet:
$$
\lambda = A \cdot \left( \frac{n^2}{n^2 - 2^2} \right) \qquad ; \qquad n \geq 3
$$
Dabei bezeichnet $A$ eine empirische Konstante, eine Wellenlänge im UV-Bereich des Spektrums mit $A = 364,568 \text{ nm}$.
Balmer hielt seine Formel für einen Spezialfall einer umfassenderen Gleichung, die auch für andere Atomsorten gültig wäre. Durch spätere Untersuchungen
wurde diese Vermutung tatsächlich bestätigt. Balmer selbst hatte allerdings für die Konstante $A$ und für die Bedeutung von $n$ in seiner Formel keine
Erklärung.
Wird die Balmer-Formel nach dem Kehrwert der Wellenlänge, der Wellenzahl $k$, wobei $k = \frac{1}{\lambda}$ ist, umgeformt, entsteht der folgende Ausdruck: \begin{align} \lambda &= A \cdot \left( \frac{n^2}{n^2 - 2^2} \right) \\ \\ \frac{1}{\lambda} &= \frac1A \cdot \left( \frac{n^2 - 2^2}{n^2} \right) \\ \\ k &= \frac1A \left( 1 - \frac{2^2}{n^2} \right) \\ \\ k &= \frac{2^2}{A} \left( \frac{1}{2^2} - \frac{1}{n^2} \right) \\ \\ k &= \frac4A \left( \frac{1}{2^2} - \frac{1}{n^2} \right) \\ \\ k &= \frac{4}{364,568 \cdot 10^{-9} \text{ m}} \left( \frac{1}{2^2} - \frac{1}{n^2} \right) \\ \\ k &= 1,09737 \cdot 10^7 \frac{1}{\text{m}} \left( \frac{1}{2^2} - \frac{1}{n^2} \right) \end{align} Darin ist die Rydberg-Konstante $R_\infty = 1,09737 \cdot 10^7 \frac{1}{\text{m}}$.
Johannes Rydberg, ein schwedischer Physiker, verallgemeinerte die Balmer-Formel in der folgenden Weise: $$ k = R_\infty \left(\frac{1}{n_1^2} - \frac{1}{n_2^2} \right) $$ Wobei $n_2 > n_1$ gilt. Das ist die sogenannte Rydberg-Formel. Für die bekannten Linien im Wasserstoffspektrum, die der Balmer-Formel zugrunde lagen, ist somit $n_1 = 2$. Mit dieser Verallgemeinerung sagte Rydberg noch zu findende Linien im Spektrum voraus. Diese zusätzlichen Linien wurden 1906 von Theodore Lyman für $n_1 = 1$ und 1908 von Friedrich Paschen für $n_1 = 3$ gefunden. Die Verallgemeinerung wurde damit also bestätigt, allerdings gab es noch keine Theorie zu dieser Formel.
Mit Hilfe des Zusammenhangs zwischen Frequenz und Wellenlänge, $\lambda \cdot f = c$, lässt sich die Rydberg-Konstante auch so schreiben: $$ f_R = c \cdot R_\infty $$ Die Konstante $f_R$ bezeichnet die sogenannte Rydberg-Frequenz mit $f_R = 3,2898 \cdot 10^{15} \text{ Hz}$.
Damit wird die Rydberg-Formel zu \begin{align} f = f_R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \end{align} So kann direkt die Frequenz der emittierten Strahlung bestimmt werden. Für die Energie der Strahlung folgt, wegen $E = h \cdot f$, \begin{align} E = h \cdot f_R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \end{align}
Bohr interpretierte die Rydberg-Formel in der Energie-Version als Differenz zweier Energiewerte, die von $n_1$ bzw. $n_2$ abhängen.
\begin{align}
\Delta E &= h f_R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \\ \\
\Delta E &= \frac{h f_R}{n_1^2} - \frac{h f_R}{n_2^2}
\end{align}
Er entwickelte das Rutherfordsche Atommodell weiter, indem er den Elektronen einzelne Energieniveaus zuordnete. Die Niveaus sind dabei
gleichbedeutend zu Bahnen, die kreisförmig um den Atomkern herum führen. Das führte wiederum zu dem Schalenmodell des Atoms, das als
Bohrsches Atommodell bekannt ist.
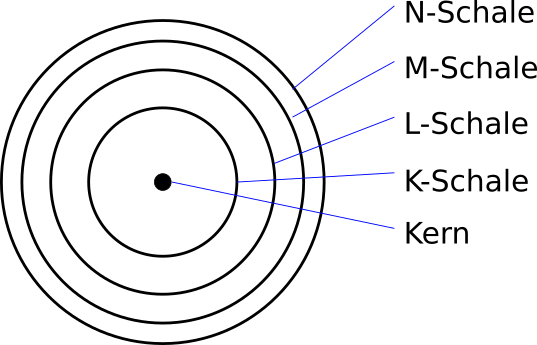
Die Schalen können als Energieniveaus interpretiert werden. Sie werden dafür von innen nach außen durchnummeriert. Die K-Schale
entspricht also $n = 1$, die L-Schale $n = 2$ usw.
Die Energiedifferenz aus der Rydberg-Formel entspricht nach diesem Modell der Energie, die notwendig ist, um ein Elektron von einer Schale auf
die nächst höhere Schale zu heben, z.B. von $n = 1$ auf $n = 2$. Sie entspricht auch der Energie, die frei wird, wenn ein Elektron von einer Schale
auf die nächst tiefere Schale fällt, z.B. von $n = 4$ auf $n = 3$.
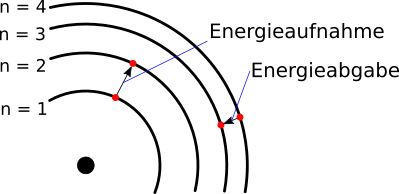
Mit der Interpretation der Schalenstruktur als Energieniveau umging Bohr das Problem, dass ein geladenes Objekt, das sich auf einer Kreisbahn bewegt, zu jedem Zeitpunkt eine Radialbeschleunigung erfahren muss, um auf der Kreisbahn zu bleiben. Deswegen muss ständig Energie aufgewendet werden, die in diesem Fall vom Objekt selbst kommen muss, indem es kinetische Energie abgibt. Es muss also immer langsamer werden, was dazu führen muss, dass die Kreisbahn einen immer kleineren Radius hätte. Das geladene Objekt würde so in kurzer Zeit in den Kern stürzen und es gäbe keine stabilen Atome. Mit den Energieniveaus hat jedes Elektron einen bestimmten Energiewert, der von der Schale abhängt, auf der sich das Elektron befindet.
Für die einzelnen Energieniveaus ergeben sich die folgenden Energiewerte: \begin{align} n &= 1: E_1 = \frac{h f_R}{1^2} = 2,18 \cdot 10^{-18} \text{ J} = 13,61 \text{ eV} \\ \\ n &= 2: E_2 = \frac{h f_R}{2^2} = 5,45 \cdot 10^{-19} \text{ J} = 3,40 \text{ eV} \\ \\ n &= 3: E_3 = \frac{h f_R}{3^2} = 2,42 \cdot 10^{-19} \text{ J} = 1,51 \text{ eV} \\ \\ &\vdots \end{align}
Die oben angegebenen Werte entstammen immer noch der empirisch erstellten Balmer-Formel und der Interpretation von Bohr. Bohr hatte allerdings
eine Theorie, mit der die empirisch gewonnenen Daten erklärt werden konnten. Dazu stellt Bohr drei Postulate vor:
1. Ein Elektron in einem Atom kann nur diskrete Energiewerte $E_n$ annehmen.
2. Wechselt ein Elektron zwischen diesen diskreten Werten, wird die Energiedifferenz als Strahlung emittiert bzw. die Energie wird absorbiert. Es
gilt: $\Delta E = h \cdot f$
3. Der Umlauf der Elektronen erfolgt auf diskreten Bahnen, auf denen sie keine Energie abstrahlen. Dafür müssen die Bahnen die folgenden Quantenbedingung
erfüllen: $2 \cdot \pi \cdot r_n \cdot m_e \cdot v_n = n \cdot h$
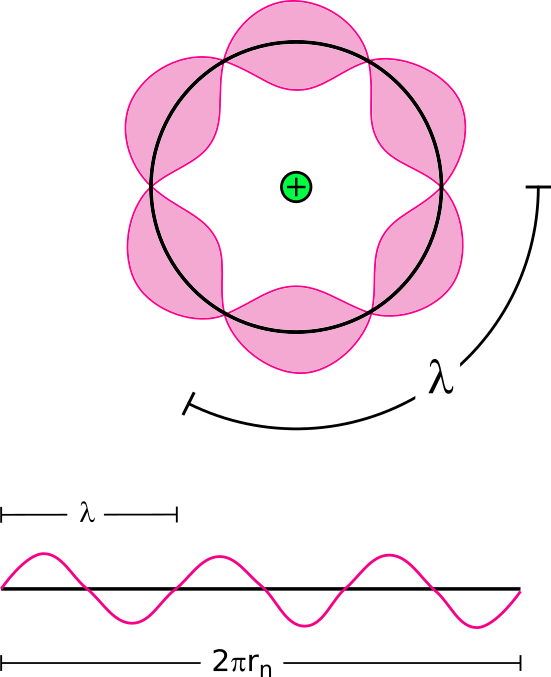Die von Bohr aufgestellte Quantenbedingung stammt aus der Überlegung, dass ein Elektron als (zeitlich stabile) Welle mit einer Wellenlänge $\lambda$
nur dann existieren kann, wenn die Länge der Kreisbahn, also der Umfang eines Kreises mit dem Radius $r_n$, einem ganzzahligen Vielfachen der
Wellenlänge entspricht. Das heißt:
\begin{align}
U_n = 2 \cdot \pi \cdot r_n &= n \cdot \lambda \qquad \qquad \mathsf{de Broglie: } \, \lambda = \frac hp = \frac{h}{m_e \cdot v_n} \\ \\
2 \cdot \pi \cdot r_n &= \frac{n \cdot h}{m_e \cdot v_n} \\ \\
2 \cdot \pi \cdot r_n \cdot m_e \cdot v_n &= n \cdot h
\end{align}
Der Wellenansatz für das Elektron auf seiner Bahn führt also zu der Quantenbedingung von Bohr.
Des weiteren kann für eine Kreisbewegung immer der folgende Ansatz gemacht werden:
$$
F_Z = F_C
$$
Die für die Kreisbewegung notwendige Zentripetalkraft kann nur durch die Coulombkraft aufgebracht werden. Also:
\begin{align}
\frac{m_e \cdot v_n^2}{r_n} &= \frac{e^2}{4 \cdot \pi \cdot \epsilon_0 \cdot r_n^2} \\ \\
m_e \cdot r_n \cdot v_n^2 &= \frac{e^2}{4 \cdot \pi \cdot \epsilon_0} \\ \\
\end{align}
Die Quantenbedingung wird mit $v_n$ multipliziert und durch $2 \cdot \pi$ geteilt:
\begin{align}
2 \cdot \pi \cdot r_n \cdot m_e \cdot v_n &= n \cdot h \\ \\
r_n \cdot m_e \cdot v_n^2 &= \frac{n \cdot h \cdot v_n}{2 \cdot \pi} \\ \\
m_e \cdot r_n \cdot v_n^2 &= \frac{n \cdot h \cdot v_n}{2 \cdot \pi}
\end{align}
Mit dem Ansatz aus der Zentripetalkraft und der Quantenbedingung folgen zwei Ausdrücke, in denen erstens die beiden unbekannten Größen
$r_n$, der Radius der Kreisbahn, und $v_n$, die Geschwindigkeit des Elektrons, vorkommen und in denen zweitens auf der jeweils linken Seite
der Gleichung derselbe Ausdruck steht. Das heißt, die rechte Seite ist auch gleich:
\begin{align}
\frac{n \cdot h \cdot v_n}{2 \cdot \pi} &= \frac{e^2}{4 \cdot \pi \cdot \epsilon_0} \\ \\
v_n &= \frac{e^2}{2 \cdot \epsilon_0 \cdot h \cdot n}
\end{align}
Der Ausdruck für die Geschwindigkeit kann nun z.B. in die Quantenbedingung eingesetzt werden:
\begin{align}
2 \cdot \pi \cdot r_n \cdot m_e \cdot v_n &= n \cdot h \\ \\
2 \cdot \pi \cdot r_n \cdot m_e \cdot \frac{e^2}{2 \cdot \epsilon_0 \cdot h \cdot n} &= n \cdot h \\ \\
r_n &= \frac{\epsilon_0 \cdot h^2 \cdot n^2}{\pi \cdot m_e \cdot e^2}
\end{align}
Beide Ausdrücke, sowohl für den Radius $r_n$ als auch für die Geschwindigkeit $v_n$ enthalten neben dem Parameter $n$ nur Konstanten.
Nach dem ersten Bohrschen Postulat besitzt ein Elektron im Atom die Energie $E_n$. Die Gesamtenergie setzt sich zusammen aus der Summe der
kinetischen Energie der Bewegung und der potentiellen Energie des Coulombfeldes (Die positive Ladung des Kerns erzeugt ein elektrisches Feld, das
sich auf das Elektron auswirkt.) Es gilt:
$$
E_n = E_{kin} + E_{pot}
$$
Für die kinetische Energie folgt:
\begin{align}
E_{kin} &= \frac12 \cdot m_e \cdot v_n^2 \\ \\
E_{kin} &= \frac12 \cdot m_e \cdot \left(\frac{e^2}{2 \cdot \epsilon_0 \cdot h \cdot n}\right)^2 \\ \\
E_{kin} &= \frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2 \cdot n^2}
\end{align}
Und für die potentielle Energie:
\begin{align}
E_{pot} &= - \frac{e^2}{4 \cdot \pi \cdot \epsilon_0 \cdot r_n} \\ \\
E_{pot} &= - \frac{e^2}{4 \cdot \pi \cdot \epsilon_0 \cdot \frac{\epsilon_0 \cdot h^2 \cdot n^2}{\pi \cdot m_e \cdot e^2}} \\ \\
E_{pot} &= - \frac{m_e \cdot e^4}{4 \cdot \epsilon_0^2 \cdot h^2 \cdot n^2}
\end{align}
Für die Gesamtenergie folgt damit:
$$
E_n = - \frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2 \cdot n^2}
$$
Mit dem zweiten Bohrschen Postulat lässt sich der Übergang eines Elektrons von einem Niveau $E_{n2}$ auf ein Niveau $E_{n1}$ folgendermaßen
schreiben:
\begin{align}
\Delta E_n &= E_{n1} - E_{n2} \\ \\
\Delta E_n &= - \frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2 \cdot n_1^2} - \left(- \frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2 \cdot n_2^2} \right) \\ \\
\Delta E_n &= - \frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2} \cdot \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right)
\end{align}
Mit dieser Gleichung wird die Rydberg-Formel begründet. In der Rydberg-Formel steht als Vorfaktor der Ausdruck $h \cdot f_R$, was dem Ausdruck
$\frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2}$ entspricht. Der Klammerausdruck ist identisch. Bohr konnte mit seinen Postulaten
der empirisch gefundenen Rydberg- bzw. Balmer-Formel eine theoretische Begründung geben.
Mit Hilfe von $E_n = - \frac{m_e \cdot e^4}{8 \cdot \epsilon_0^2 \cdot h^2 \cdot n^2}$ können die einzelnen Energiewerte bestimmt und
in dem Energieniveauschema notiert werden.
Die Differenz $E_\infty - E_1$ entspricht der Energie, die dem Elektron im Grundzustand hinzugefügt werden muss, um es aus dem Atom herauszuheben. Diese Energie nennt man auch Ionisierungsenergie. In dem Fall handelt es sich um ein einfach positiv geladenes Wasserstoffatom, ein $H^+$-Ion.
© mondbrand MMXIX