Lösung zu Aufgabe 2 (Elektrische Felder)
Ein Kügelchen $(m = 50 \text{ g})$ trägt die Ladung $q = -10 \text{ nC}$ und hängt an einem Faden der Länge $l = 1 \text{ m}$. Das Kügelchen
befindet sich im homogenen Feld eines Plattenkondensators mit dem Plattenabstand $d = 10 \text{ cm}$. Zwischen den Kondensatorplatten
liegt eine Spannung von $U = 150 \text{ V}$ an.
a) Bestimmen Sie die Stärke des homogenen elektrischen Feldes.
b) Berechnen Sie den Ausschlag der Kugel.
Es geht um einen Plattenkondensator. Für diesen gilt der Zusammenhang: $$ E = \frac{U}{d} $$ Mit den Werten für $U = 150 \text{ V}$ und $d = 10 \text{ cm} = 0,1 \text{ m}$ folgt für die Feldstärke: \begin{align} E &=\frac{150 \text{ V}}{0,1 \text{ m}} \\ E &= 1500 \, \frac{\text{V}}{\text{m}} \end{align}
Für den Ausschlag des Kügelchens zunächst eine Skizze für die Ausgangssituation und für die Situation, dass das Feld das Kügelchen ausgelenkt hat:
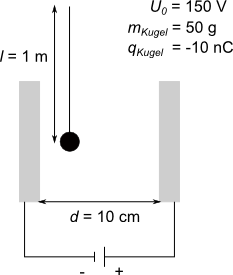
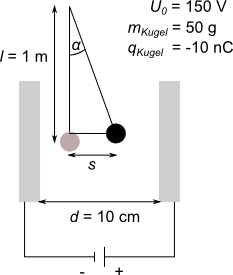
Aus den Skizzen folgt zunächst die Überlegung, dass sich das Kügelchen im ausgelenkten Zustand nicht mehr bewegt. Aus einem konstanten
Bewegungszustand (Stillstand) folgt, dass sich der Körper in einem Kräftegleichgewicht befindet. Die Kräfte, die hier auf das Kügelchen wirken,
sind die Gewichtskraft $F_G$ und die Coulomb-Kraft $F_C$.
Um dies zu verdeutlichen, benutzt man das sogenannte Kräftebild. Analog zu der tatsächlichen Situation werden nur die wirkenden Kräfte gezeichnet. In
dem vorliegenden Fall sieht das so aus, wie links gezeigt.
Für die wirkende Gewichtskraft berechnet man
\begin{align}
F_G &= m \cdot g \\
F_G &= 50 \text{ g} \cdot 9,81 \, \frac{\text{m}}{\text{s}^2} \\
F_G &= 0,05 \text{ kg} \cdot 9,81 \, \frac{\text{m}}{\text{s}^2} \\
F_G &= 0,4905 \text{ N}
\end{align}
Die Coulomb-Kraft ist
\begin{align}
F_C &= E \cdot q \\
F_C &= 1500 \, \frac{\text{V}}{\text{m}} \cdot \left( - 10 \text{ nC} \right) \\
F_C &= 1500 \, \frac{\text{N}}{\text{C}} \cdot \left( - 10 \cdot 10^{-9} \text{ C} \right) \\
F_C &= - 1,5 \cdot 10^{-5} \text{ N}
\end{align}
Das negative Vorzeichen für die Coulomb-Kraft rührt daher, das eine Kraft mit positivem Vorzeichen diejenige Kraft ist, die auf eine positive Probeladung wirkt.
Hier wäre das eine Kraft, die in Richtung der negativen Kondensatorplatte wirkt. Da aber eine negative Probeladung vorliegt, hat die wirkende
Coulomb-Kraft auch ein negatives Vorzeichen. Die Skizze im Kraft-Bild zeigt aber die tatsächliche Wirkungsrichtung an.
Der in den Skizzen auftauchende Winkel $\alpha$ taucht in der Darstellung der tatsächlichen Situation folgendermaßen auf:
$$
\sin \left( \alpha \right) = \frac{s}{l}
$$
Im Kraft-Bild taucht er hingegen so auf:
$$
\tan \left( \alpha \right) = \frac{F_C}{F_G}
$$
Unter der Berücksichtigung, dass der Winkel $\alpha$ klein ist, bzw. dass der Ausschlag klein ist gegenüber der Fadenlänge, gilt die sogenannte
Kleinwinkelnäherung: $\sin \left( \alpha \right) \approx \tan \left( \alpha \right)$
Damit erhält man:
\begin{align}
\frac{s}{l} &= \frac{F_C}{F_G} \\
s &= \frac{F_C}{F_G} \cdot l \\
s &= \frac{E \cdot q}{m \cdot g} \cdot l \\
s &= \frac{1,5 \cdot 10^{-5} \text{ N}}{0,4905 \text{ N}} \cdot 1 \text{ m} \\
s &= 3 \cdot 10^{-5} \text{ m}
\end{align}