Lösung zu Aufgabe 6 (Elektrische Felder)
Zwei Ladungen $Q_1$ und $Q_2$ befinden sich in einem Abstand von $10 \text{ cm}$ voneinander.
Es seien $Q_1 = 5 \text{ nC}$ und $Q_2 = 10 \text{ nC}$.
a) Berechnen Sie die Kraft, die auf eine Probeladung $q = 1 \text{ nC}$ in der Mitte zwischen den Ladungen wirkt.
b) Bestimmen Sie die Position der Probeladung, an der keine Kraft auf sie wirkt.
c) Skizzieren Sie aufgrund ihrer Ergebnisse das elektrische Feld.
Die Kraft ist eine gerichtete Größe, die aufgrund des Superpositionsprinzips unabhängig voneinander berechnet und im Anschluss zusammengefasst werden kann. Damit berechnet man zunächst die Kraft, die die Ladung $Q_1$ auf die Probeladung ausübt, danach die Kraft, die durch die Ladung $Q_2$ auf die Probeladung ausgeübt wird. Zum Schluss werden beide (Einzel-)Kräfte zu einer resultierenden (Gesamt-)Kraft zusammengefasst.
Für die Ladung $Q_1$: \begin{align} F_1 &= \frac{1}{4 \cdot \pi \cdot \epsilon_0} \cdot \frac{Q_1 \cdot q}{r^2} \\ \\ F_1 &= \frac{1}{4 \cdot \pi \cdot \epsilon_0} \cdot \frac{5 \text{ nC} \cdot 1 \text{ nC}}{\left( 5 \text{ cm} \right)^2} \\ F_1 &= 1,80 \cdot 10^{-5} \text{ N} \end{align} Da beide Ladungen positiv sind, handelt es sich um eine abstoßende Kraft. Sie weist also am Ort der Probeladung von $Q_1$ weg.
Für die Ladung $Q_2$: \begin{align} F_2 &= \frac{1}{4 \cdot \pi \cdot \epsilon_0} \cdot \frac{Q_2 \cdot q}{r^2} \\ \\ F_2 &= \frac{1}{4 \cdot \pi \cdot \epsilon_0} \cdot \frac{10 \text{ nC} \cdot 1 \text{ nC}}{\left( 5 \text{ cm} \right)^2} \\ F_2 &= 3,60 \cdot 10^{-5} \text{ N} \end{align} Da auch hier beide Ladungen positiv sind, weist die Kraft am Ort der Probeladung von $Q_2$ weg.
Die Probeladung befindet sich zwischen den Feldladungen, d.h. die drei Ladungen liegen auf einer Linie. Damit liegen die wirkenden Kräfte auch auf einer Linie. Sie können also einfach addiert werden, wenn berücksichtigt wird, dass sie in die entgegengesetzten Richtungen weisen. Es folgt also: \begin{align} F &= F_1 + (- F_2) \\ F &= 1,80 \cdot 10^{-5} \text{ N} - 3,60 \cdot 10^{-5} \text{ N} \\ F &= - 1,80 \cdot 10^{-5} \text{ N} \end{align} Die Kraft, die insgesamt auf die Probeladung wirkt, beträgt $1,8 \cdot 10^{-5} \text{ N}$. Das Vorzeichen berücksichtigt lediglich die Richtung der Kraftwirkung, die hier aber nicht gefragt war.
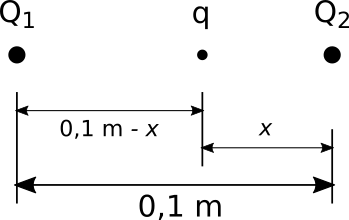Die allgemeine Situation mit der Probeladung zwischen den Feldladungen sieht etwa so wie in der Abbildung aus. Der Abstand der Probeladung von einer
Feldladung (hier: $Q_2$) ist x, der Abstand von der anderen Feldladung $Q_1$ entsprechend 0,1 - x.
Da die Probeladung kräftefrei sein soll, müssen sich die beiden Coulombkräfte aufgrund der Feldladungen gegenseitig aufheben. Es gilt also: $$ F_1 = F_2 $$ Für die jeweiligen Abstände $r$ in den Ausdrücken für $F_1$ uns $F_2$ setzt man dann entsprechend $x$, bzw. $0,1 - x$ ein: \begin{align} \frac{1}{4 \cdot \pi \cdot \epsilon_0} \cdot \frac{Q_1 \cdot q}{\left(0,1 - x \right)^2} &= \frac{1}{4 \cdot \pi \cdot \epsilon_0} \cdot \frac{Q_2 \cdot q}{x^2} \\ \\ \frac{Q_1 \cdot q}{4 \cdot \pi \cdot \epsilon_0} \cdot x^2 &= \frac{Q_2 \cdot q}{4 \cdot \pi \cdot \epsilon_0} \cdot \left(0,1 - x \right)^2 \\ \end{align} Der Ausdruck $\frac{q}{4 \cdot \pi \cdot \epsilon_0}$ ist auf beiden Seiten der Gleichung identisch und kürzt sich somit heraus. Es verbleibt: \begin{align} Q_1 \cdot x^2 &= Q_2 \cdot \left(0,1 - x \right)^2 \\ \frac{Q_1}{Q_2} \cdot x^2 &= 0,01 - 0,2 \cdot x + x^2 \\ \left( \frac{Q_1}{Q_2} - 1 \right) \cdot x^2 + 0,2 \cdot x - 0,01 &= 0 \\ \\ x^2 + \frac{0,2}{\left( \frac{Q_1}{Q_2} - 1 \right)} \cdot x - \frac{0,01}{\left( \frac{Q_1}{Q_2} - 1 \right)} &= 0 \\ \\ x_{1,2} &= 0,2 \pm \sqrt{0,04 - 0,02} \\ x_1 &= 0,34 \\ x_2 &= 0,06 \end{align} Die erste Lösung führt zu einem Punkt, der außerhalb der beiden Feldladungen liegt. Diese Lösung wird hier vernachlässigt. Die zweite Lösung führt zu dem Punkt, an dem sich die Kräfte auf eine Probeladung gegenseitig aufheben. Der Punkt hat von der Ladung $Q_2$ den Abstand 6 cm und von der Ladung $Q_1$ den Abstand 4 cm.