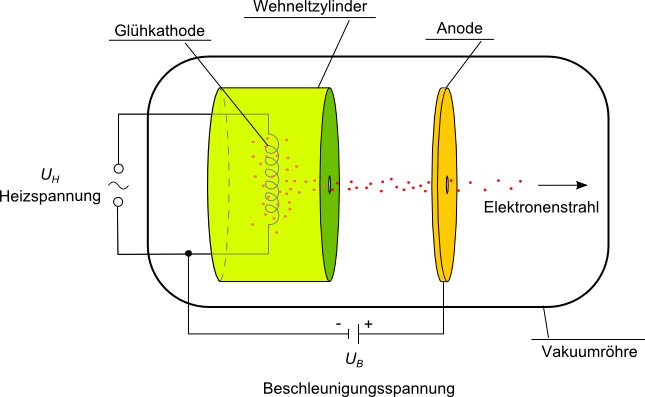
Wird ein Glühdraht an eine geringe Wechselspannung (ca. 4 - 6 V; Heizspannung $U_H$) angeschlossen, bewegen sich die Elektronen innerhalb des Drahtes ständig hin und her.
Dabei stoßen sie an die Atomrümpfe und erzeugen Wärme; der Draht fängt an zu glühen. Einzelne Elektronen erhalten durch die Stöße genug Energie um den
Atomverband des Drahtes zu verlassen. Es entsteht eine Elektronenwolke um den Draht herum. Die Elektronen in der Wolke haben unterschiedlich viel
Energie, sie bewegen sich also mit unterschiedlichen Geschwindigkeiten in alle möglichen Richtungen.
Zwischen dem Glühdraht und einer Metallplatte mit einem Loch in der Mitte wird eine Gleichspannung angelegt (mehrere kV; Beschleunigungsspannung $U_B$). Der Draht wird als Kathode, die Metallplatte als Anode angeschlossen. Dadurch werden die freien Elektronen zu der Anode hin beschleunigt. Da sie sich aber überall um den Draht herum befinden, würden sie sich auch relativ ungeordnet in Richtung Anode bewegen.
Um die Elektronen zu fokussieren, wird zwischen Draht und Metallplatte der sogenannte Wehneltzylinder eingesetzt. Durch eine geringe negative Spannung werden die Elektronen von allen Seiten des Zylinders abgestoßen. Durch die enorme Anziehungskraft der Anode werden sie so nach und nach alle durch das Loch in der Mitte des Zylinders gedrängt. So entsteht ein fokussierter Strahl einzelner Elektronen mit einer bestimmten, durch die Beschleunigungsspannung einstellbaren Geschwindigkeit.
Der ganze Aufbau muss sich in einem Vakuum befinden, da die Elektronen durch Stöße mit den Luftmolekülen in alle Richtungen abgelenkt und nach der Anode auch ihre Geschwindigkeit verlieren würden.
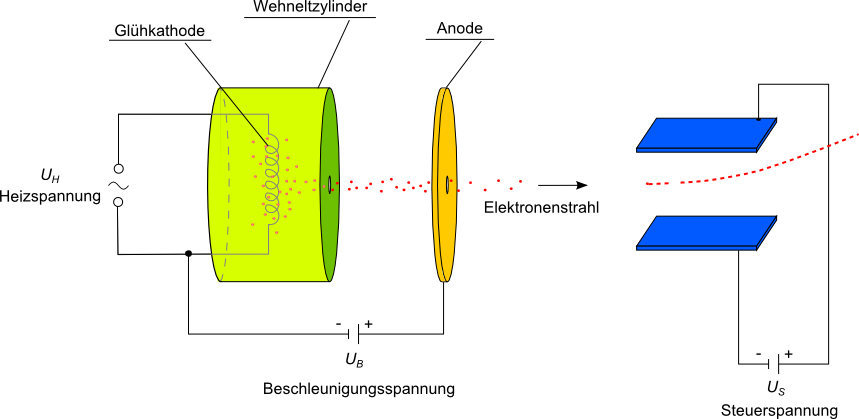
Das eigentliche Ablenksystem besteht aus zwei Platten einer Plattenkondensatoranordnung. Die Elektronen treten mittig in den Plattenkondensator
ein und werden durch die im Kondensator herrschenden Feldkräfte abgelenkt.
Mit zwei Anordnungen hintereinander können die Elektronen zunächst nach oben und unten (vertikal) abgelenkt werden und anschließend nach rechts und links (horizontal). So kann durch eine entsprechende Regelung der Steuerspannungen an den Kondensatorplatten ein Bildschirm am Ende der Vakuumröhre Punkt für Punkt mit Elektronen beschossen werden.
Die Braunsche Röhre wurde im Jahre 1897 von Karl Ferdinand Braun entwickelt. Er erhielt gemeinsam mit Guglielmo Marconi für die Leistungen in der Funk- und
Fernsehtechnik 1909 den Physiknobelpreis.
Die Röhre ist unten als Prinzipskizze abgebildet. Sie bildete die Grundlage für die Fernsehtechnik bis ins 21. Jahrhundert hinein und aktuell auch
noch für den Betrieb von Oszilloskopen.
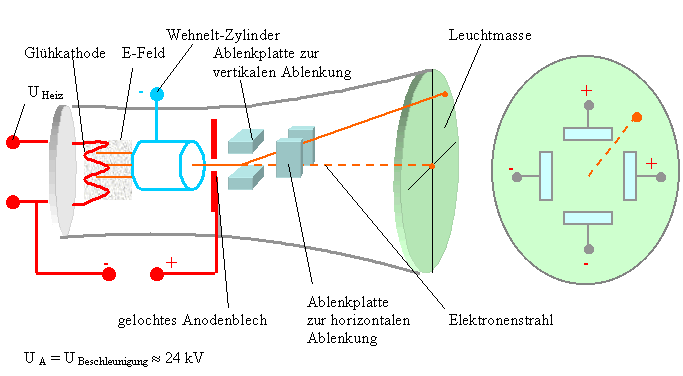
Eine Glühkathode emittiert Elektronen, die durch eine Spannung von 2 kV zur Anode hin beschleunigt werden.
Für die Bewegung der Elektronen gilt die Energieerhaltung, d.h., die kinetische Energie der Elektronen an der Anode entspricht der elektrischen Energie, die durch die Spannung geliefert wird. Es gilt: \begin{align} W_C &= E_{kin} \\ q \cdot U &= \frac{1}{2} \cdot m \cdot v^2 \\ e \cdot U &= \frac{1}{2} \cdot m_e \cdot v^2 \\ v &= \sqrt{\frac{2 \cdot e \cdot U}{m_e}} \\ \\ v &= \sqrt{\frac{2 \cdot 1,602 \cdot 10^{-19} \text{ C} \cdot 2000 \text{ V}}{9,1 \cdot 10^{-31} \text{ kg}}} \\ v &= 2,65 \cdot 10^7 \frac{\text{ m}}{\text{ s}} \end{align}
Ein Elektron mit der Geschwindigkeit $v_x = 2,65 \cdot 10^7 \frac{\text{ m}}{\text{ s}}$ tritt senkrecht zu den Feldlinien mittig in einen Plattenkondensator ein. Der Kondensator hat die Länge $l = 2 \text{ cm}$, die Platten haben einen Abstand $d = 1 \text{ cm}$. Am Kondensator liegt eine Spannung von $U = 200 \text{ V}$ an.
Für die Zeit, die das Elektron für den Durchflug durch den Kondensator benötigt, gilt: \begin{align} t &= \frac{s_x}{v_x} \\ t &= \frac{x}{v_x} \\ \\ t &= \frac{2 \cdot 10^{-2} \text{ m}}{2,65 \cdot 10^7 \frac{\text{ m}}{\text{ s}}} \\ t &= 7,55 \cdot 10^{-10} \text{ s} \end{align} Während dieser Zeit wirkt auf das Elektron die Coulombkraft $F_C$ des elektrischen Feldes. Es gilt: \begin{align} F_C &= q \cdot E \\ F_C &= e \cdot \frac{U}{d} \\ \\ F_C &= 1,602 \cdot 10^{-19} \text{ C} \cdot \frac{200 \text{ V}}{1 \cdot 10^{-2} \text{ m}} \\ F_C &= 3,20 \cdot 10^{-15} \text{ N} \end{align} Es gilt weiterhin: \begin{align} F &= m \cdot a \\ a &= \frac{F}{m} \\ a &= \frac{F_C}{m_e} \\ \\ a &= \frac{3,20 \cdot 10^{-15} \text{ N}}{9,1 \cdot 10^{-31} \text{ kg}} \\ a &= 3,52 \cdot 10^{15} \frac{\text{ m}}{\text{ s}^2} \end{align} Die Beschleunigung erfolgt in Richtung der positiven Kondensatorplatte, z.B. nach oben. Für die Bewegung in y-Richtung folgt: \begin{align} y &= \frac{1}{2} \cdot a \cdot t^2 \\ \\ y &= \frac{1}{2} \cdot 3,52 \cdot 10^{15} \frac{\text{ m}}{\text{ s}^2} \cdot \left( 7,55 \cdot 10^{-10} \text{ s} \right)^2 \\ y &= 1,00 \cdot 10^{-3} \text{ m} \end{align} In einem allgemeinen Fall erhält man für die Bewegung eines geladenen Teilchens der Masse m in einem homogenen elektrischen Feld (senkrecht zur ursprünglichen Bewegung in x-Richtung) den folgenden Term: \begin{align} y = \frac{q \cdot U}{2 \cdot d \cdot m \cdot v_x^2} \cdot x^2 \end{align} Das Teilchen bewegt sich also auf einer parabelförmigen Bahn, wenn es sich zwischen den Kondensatorplatten befindet.
Für die Geschwindigkeit in y-Richtung erhält man: \begin{align} v_y &= a \cdot t \\ \\ v_y &= 3,52 \cdot 10^{15} \frac{\text{ m}}{\text{ s}^2} \cdot 7,55 \cdot 10^{-10} \text{ s} \\ v_y &= 2,66 \cdot 10^6 \frac{\text{ m}}{\text{ s}} \end{align} Der Elektronenstrahl tritt unter dem Winkel $\alpha$ aus dem Kondensator aus. Für den gilt: \begin{align} \alpha &= tan^{-1} \left( \frac{v_y}{v_x} \right) \\ \\ \alpha &= tan^{-1} \left( \frac{2,66 \cdot 10^6 \frac{\text{ m}}{\text{ s}}}{2,65 \cdot 10^7 \frac{\text{ m}}{\text{ s}}} \right) \\ \alpha &= 5,73 ^{ \circ} \end{align}
© mondbrand MMXIX