

Bei der Erstellung von Gleichstromkreisen gibt es eine Liste von Symbolen, die zu verwenden sind. Dazu sollte beachtet werden, dass nur senkrechte oder waagerechte Linien gezeichnet werden.
Die Symbole und ihre Bedeutung:
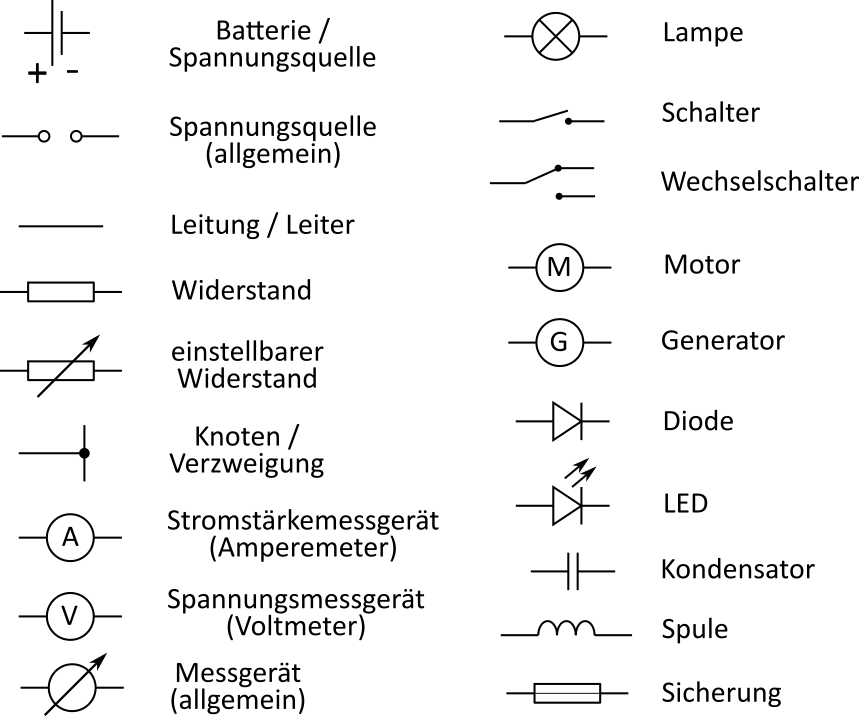
Unverzweigt bedeutet, dass es nur einen Strompfad gibt, der von der Spannungsquelle bis zur Spannungsquelle verläuft, und dabei ein oder mehrere Bauteile (Verbraucher) durchläuft. Die Verbraucher sind in Reihe verschaltet.
Ein solcher Stromkreis wird auch Masche genannt. Für eine Masche gilt:
Die Summe aller Spannungen, die über den Verbrauchern abfallen ist gleich der Speisespannung.
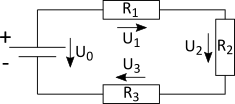
In dem gezeigten Beispiel führt das zu der folgenden Gleichung:
Zweite Kirchhoffsche Regel (Maschenregel):
$$ U_1 + U_2 + U_3 = U_0 \\ \\ U_1 + U_2 + U_3 - U_0 = 0 $$Weiterhin gilt, dass die Stromstärke an jeder Stelle des unverzweigten Stromkreises konstant bleibt. Es gilt also $$ I_0 = I_1 = I_2 = I_3 $$
Mit der Gleichung $U = R \cdot I$ führt das zu $$ R_1 \cdot I_1 + R_2 \cdot I_2 + R_3 \cdot I_3 = R_E \cdot I_0 \\ \\ \left( R_1 + R_2 + R_3 \right) \cdot I = R_E \cdot I $$ $R_E$ bezeichnet dabei einen sogenannten Ersatzwiderstand, der lediglich virtuell vorhanden ist und der alle sich in einem Stromkreis befindlichen Widerstände zusammenfasst. Der Ansatz ist dabei, dass einzelne Ströme und Spannungen, die in einem Stromkreis auftreten, so besser berechnet werden können.
Der Ersatzwiderstand lässt sich also so bestimmen: $$ R_E = R_1 + R_2 + ... + R_n $$ Das gilt für n Widerstände, die in Reihe geschaltet sind.
Damit wird der oben gezeigte Stromkreis umgewandelt in einen Ersatzstromkreis:
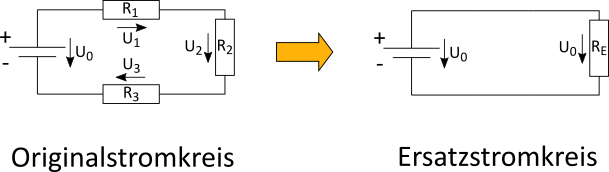
Beispiel
Es seien $R_1 = 150 \; \Omega, R_2 = 200 \; \Omega, R_3 = 400 \; \Omega$ und $U_0 = 15 \text{ V}$. Dann ergibt sich für die Stromstärke:
\begin{align} I &= \frac{U_0}{R_E} \\ \\ R_E &= R_1 + R_2 + R_3 \\ R_E &= 150 \; \Omega + 200 \; \Omega + 400 \; \Omega \\ R_E &= 750 \; \Omega \\ \\ I &= \frac{15 \text{ V}}{750 \; \Omega} \\ I &= 0,02 \text{ A} = 20 \text{ mA} \end{align}Damit können alle Spannungen, die über den Widerständen abfallen, bestimmt werden:
\begin{align} U_1 &= R_1 \cdot I \\ U_1 &= 150 \; \Omega \cdot 0,02 \text{ A} \\ U_1 &= 3 \text{ V} \\ \\ U_2 &= R_2 \cdot I \\ U_2 &= 200 \; \Omega \cdot 0,02 \text{ A} \\ U_2 &= 4 \text{ V} \\ \\ U_3 &= R_3 \cdot I \\ U_3 &= 400 \; \Omega \cdot 0,02 \text{ A} \\ U_3 &= 8 \text{ V} \end{align}Die Summe aller drei Spannungen ist gleich der Speisespannung $\left( 3 \text{ V} + 4 \text{ V} + 8 \text{ V} = 15 \text{ V} \right)$. Wichtig ist hier, dass die Stromstärke durch alle Widerstände konstant ist $\left( I = I_1 = I_2 = I_3 = 0,02 \text{ A} \right)$.
Verzweigt bedeutet, dass es nur einen Strompfad gibt, der sich in zwei oder mehrere Pfade aufteilt. Der durch den Pfad fließende Strom teilt sich auf, fließt gleichzeitig durch die Verbraucher in dem jeweiligen Pfad, und vereinigt sich anschließend wieder zu einem Strompfad. Die Verbraucher sind parallel verschaltet.
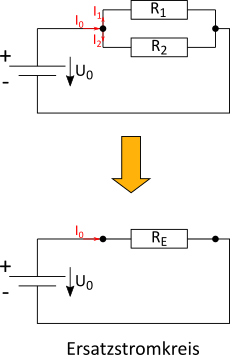
Die Aufteilung des Stroms findet an den Knoten statt. Die Knoten können keinen Strom speichern oder entstehen lassen. Daher muss gelten, dass alle Ströme, die in einen Knoten hineinfließen, auch wieder herausfließen müssen. Es gilt:
Erste Kirchhoffsche Regel (Knotenregel):
$$ I_0 = I_1 + I_2 \\ \\ I_0 - I_1 - I_2 = 0 $$Die Knoten sind jeweils mit einer Seite der Spannungsquelle verbunden. Daher fällt zwischen den Knoten genau die Spannung $U_0$ ab. Deswegen fällt auch über jedem der Widerstände die Spannung $U_0$ ab. Es gilt: $U_0 = U_1 = U_2$
Daraus folgt:
\begin{align} I_0 &= I_1 + I_2 \\ \\ \frac{U_0}{R_E} &= \frac{U_1}{R_1} + \frac{U_2}{R_2} \\ \frac{1}{R_E} \cdot U_0 &= \left( \frac{1}{R_1} + \frac{1}{R_2} \right) \cdot U_0 \\ \\ \frac{1}{R_E} &= \frac{1}{R_1} + \frac{1}{R_2} \end{align}Das ist die Berechnungsvorschrift für den Ersatzwiderstand, wenn es sich um parallel verschaltete Widerstände handelt.
Beispiel
Es seien $R_1 = 200 \; \Omega, R_2 = 400 \; \Omega$ und $U_0 = 10 \text{ V}$. Dann folgt: \begin{align} I_0 &= \frac{U_0}{R_E} \\ \\ \frac{1}{R_E} &= \frac{1}{R_1} + \frac{1}{R_2} \\ \frac{1}{R_E} &= \frac{1}{200 \; \Omega} + \frac{1}{400 \; \Omega} \\ \frac{1}{R_E} &= \frac{3}{400 \; \Omega} \\ R_E &= 133,3 \; \Omega \\ \\ I_0 &= \frac{10 \text{ V}}{133,3 \; \Omega} \\ I_0 &= 0,075 \text{ A} = 75 \text{ mA} \end{align} Und weiter: \begin{align} I_1 &= \frac{U_1}{R_1} \\ I_1 &= \frac{10 \text{ V}}{200 \; \Omega} \\ I_1 &= 0,05 \text{ A} \\ \\ I_2 &= \frac{U_2}{R_2} \\ I_2 &= \frac{10 \text{ V}}{400 \; \Omega} \\ I_2 &= 0,025 \text{ A} \\ \\ I_0 &= I_1 + I_2 \\ I_0 &= 0,05 \text{ A} + 0,025 \text{ A} \\ I_0 &= 0,075 \text{ A} \end{align} Das wäre in diesem speziellen Fall auch ein alternativer Weg, um $I_0$ zu bestimmen.
Die erste Kirchhoffsche Regel
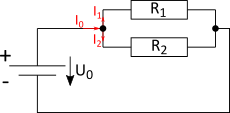
Die Summe aller in einen Knoten hineinfließenden Ströme ist gleich der Summe aller aus dem Knoten herausfließender Ströme.
$I_0 = I_1 + I_2$
Die zweite Kirchhoffsche Regel

Die Summe aller Spannungen, die in einer Masche abfallen ist gleich der Speisespannung.
$U_1 + U_2 + U_3 = U_0$
Widerstände in Reihenschaltung
Der Ersatzwiderstand ist gleich der Summe der Einzelwiderstände.
$R_E = R_1 + R_2 + R_3 + ... + R_n$
Widerstände in Parallelschaltung
Der Kehrwert des Ersatzwiderstands ist gleich der Summe der Kehrwerte der Einzelwiderstände.
$\frac{1}{R_E} = \frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+ ... + \frac{1}{R_n}$
© mondbrand MMXIX