Näherung für kleine Winkel

Die sogenannte Kleinwinkelnäherung vereinfacht viele Ausdrücke und Ansätze und ermöglicht oft erst eine akzeptable Vorgehensweise bei der Bearbeitung von Aufgaben.
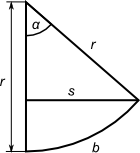
Die Näherung lautet: \begin{align} sin \, \alpha &\approx \alpha \\ sin \, \alpha &\approx tan \, \alpha \end{align} In der Abbildung sind die für die Näherung wesentlichen Ausdrücke gezeigt. Intuitiv lässt sich erkennen, dass für kleine Winkel $\alpha$ die Längen $s$ und $b$ ungefähr gleich groß sind und dass im rechtwinkligen Dreieck in der Abbildung die Hypothenuse ungefähr so lang ist wie die Ankathete.
Allgemein werden $s$ und $b$ so berechnet: \begin{align} sin \, \alpha &= \frac{s}{r} \\ s &= r \cdot sin \, \alpha \\ \\ b &= r \cdot \frac{\pi}{180^\circ} \cdot \alpha \end{align} Mit der folgenden Tabelle soll die Ähnlichkeit von $s$ und $b$ gezeigt werden:

$\alpha$	$s$	$b$
0	0	0
0,1	0,0017	0,0017
0,2	0,0035	0,0035
0,3	0,0052	0,0052
0,4	0,0070	0,0070
0,5	0,0087	0,0087
1,0	0,0175	0,0175
2,0	0,0349	0,0349
3,0	0,0523	0,0523
4,0	0,0698	0,0698
5,0	0,0872	0,0873
10,0	0,1736	0,1745
15,0	0,2588	0,2618