

Für die Untersuchung des Ladevorgangs muss zunächst der Stromkreis definiert werden. Es handelt sich um einen sogenannten RC-Kreis, ein Kreis,
in dem eine Spannungsquelle, ein Widerstand $R$ und ein Kondensator $C$ enthalten sind. In der Abbildung ist ein solcher RC-Kreis zu sehen.
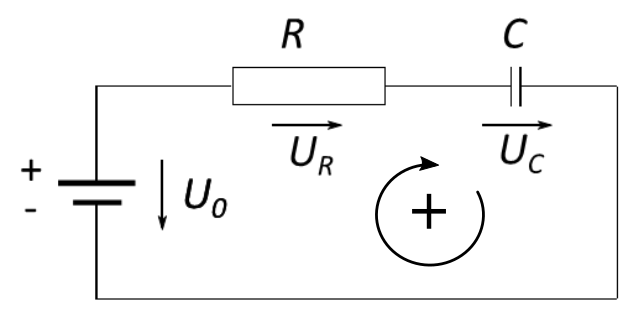
Der Maschenumlauf besagt nun, wie sich die Spannungen, die in einem solchen Kreis an jedem Bauteil abfallen, addieren. Die Pfeile in der Abbildung zeigen an, in welche Richtung die Spannung jeweils abfällt. Mit der Beachtung der Richtung ergibt es sich , dass die Summe der Spannung der beiden Verbraucher gleich der Quellspannung sein muss. Mit $$ - U_0 + U_R + U_C = 0 $$ folgt also: $$ U_0 = U_R + U_C $$
Was passiert an dem Widerstand $U_R$? Nach dem ohmschen Gesetz gilt dort: $$ U = R \cdot I $$ Die Spannung ist proportional zum Stromfluss. Der Stromfluss wiederum ist die Bewegung von Ladung pro Zeit. Es gilt also: $$ I = \frac{\Delta Q}{\Delta t}$$ Zusammengefasst heißt das für die Spannung über den Widerstand: $$ U_R = R \cdot \frac{\Delta Q}{\Delta t} $$
Für die Spannung, die über dem Kondensator abfällt, gilt: $$ U_C = \frac{Q}{C} $$ Damit erhält man für den gesamten Maschenumlauf die folgende Gleichung: $$ U_0 = R \cdot \frac{\Delta Q}{\Delta t} + \frac{Q}{C} $$
In dieser Gleichung kommt sowohl die Ladung $Q$ als auch die zeitliche Veränderung der Ladung $\frac{\Delta Q}{\Delta t}$ vor. Eine Gleichung dieser Art nennt man Differentialgleichung (Dgl).
Eine Differentialgleichung wird nicht durch Zahlen gelöst, sondern durch Funktionen. Hier ist eine Funktion gesucht, die die zeitliche Veränderung der Ladung und die Ladungsmenge beschreibt. Für Differentialgleichungen gibt es eine Vielzahl von Lösungswegen, die, jeweils angepasst an die Art der Dgl, durch einen bestimmten Algorithmus beschrieben werden.
Eine Dgl der Form $$U_0 = R \cdot \frac{\Delta Q}{\Delta t} + \frac{Q}{C}$$ hat für den Ladevorgang die folgende Lösung: \begin{align} Q(t) &= C U_0 \left( 1 - e^{- \frac{t}{RC}} \right) \\ \\ Q(t) &= Q_0 \left( 1 - e^{- \frac{t}{RC}} \right) \end{align}
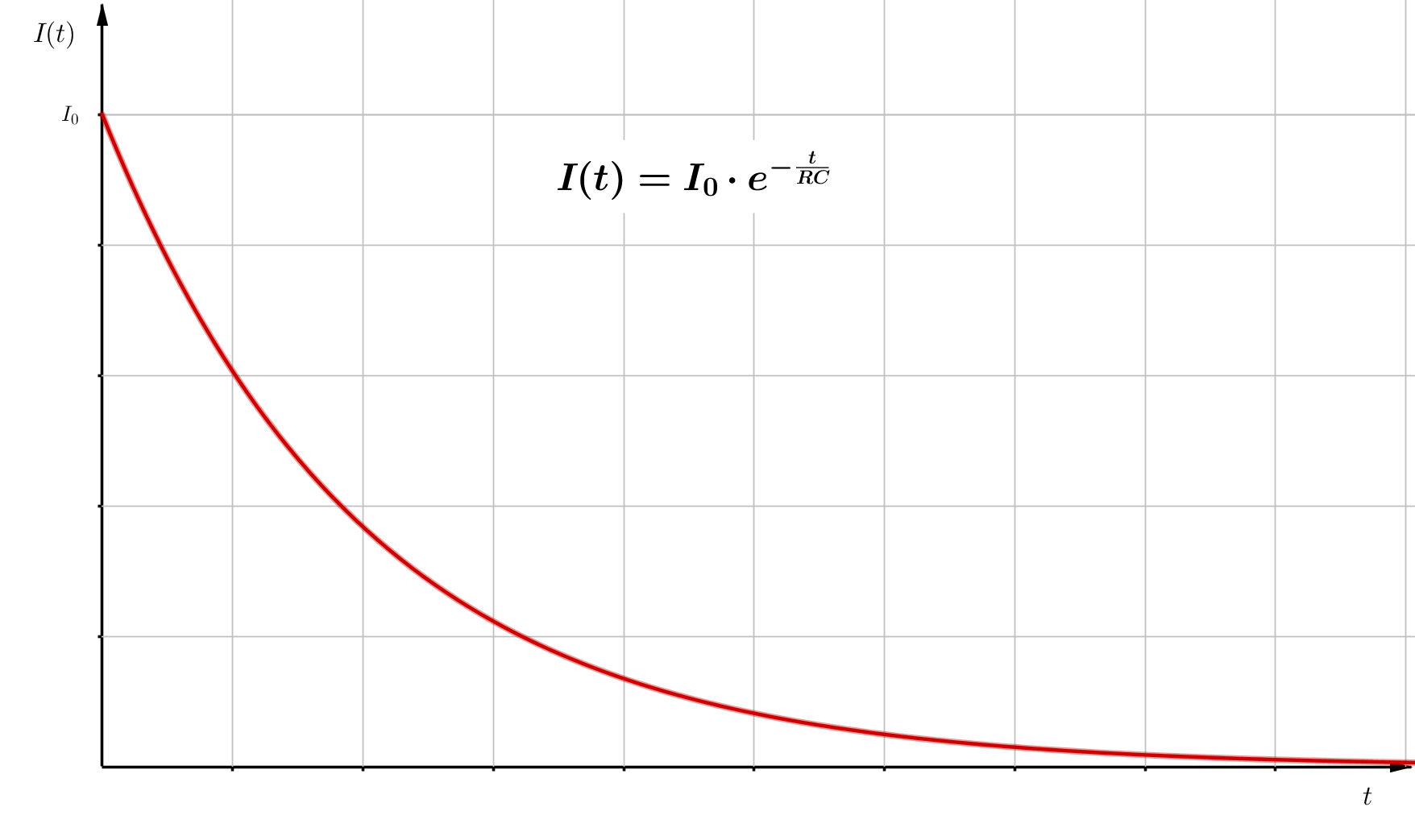
Die Stromstärke ist durch die Änderung der Ladung gegeben. Damit folgt für die zeitabhängige Stromstärke der folgende Ausdruck: \begin{align} I(t) &= \frac{dQ}{dt} \\ \\ I(t) &= \frac{Q_0}{RC} \cdot e^{- \frac{t}{RC}} \\ \\ I(t) &= I_0 \cdot e^{- \frac{t}{RC}} \end{align}
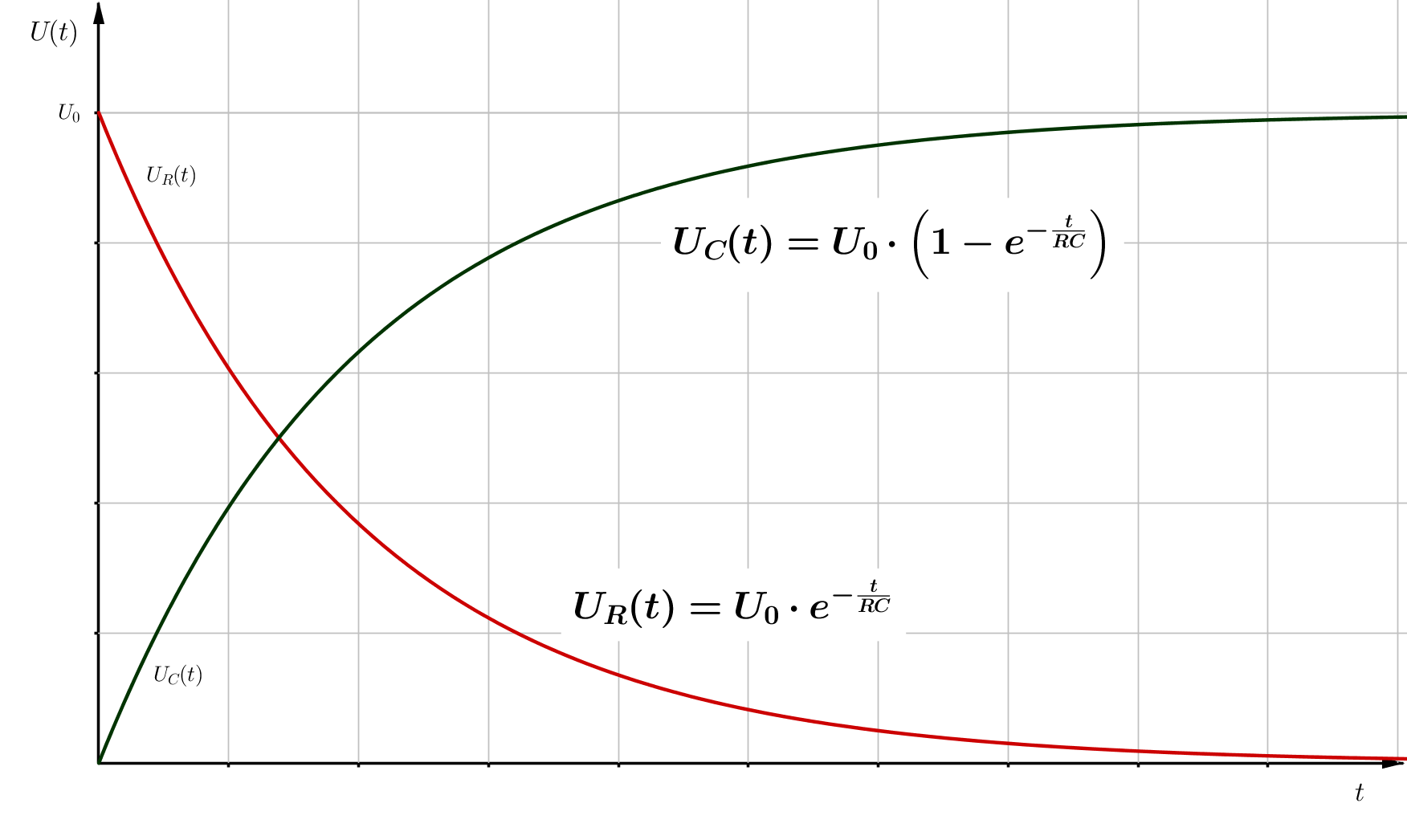
Damit folgt, dass in einem RC-Kreis zunächst ein Strom $I_0$ fließt, der durch den Widerstand $R$ und die Speisespannung $U_0$ gegeben ist. Im weiteren zeitlichen Verlauf sinkt die Stromstärke bis auf Null ab. Das geschieht dann, wenn der Kondensator komplett aufgeladen ist und die Spannung, die über dem Kondensator abfällt, der Speisespannung entspricht. Über dem Widerstand fällt dann keine Spannung ab. \begin{align} U_R(t) &= R \cdot I(t) \\ \\ U_R(t) &= R \cdot I_0 \cdot e^{- \frac{t}{RC}} \\ \\ U_R(t) &= U_0 \cdot e^{- \frac{t}{RC}} \end{align} für die Spannung über dem Widerstand und \begin{align} U_C(t) &= \frac{Q(t)}{C} \\ \\ U_C(t) &= \frac{C U_0}{C} \cdot \left( 1 - e^{- \frac{t}{RC}} \right) \\ \\ U_R(t) &= U_0 \cdot \left( 1 - e^{- \frac{t}{RC}} \right) \end{align} für die Spannung über dem Kondensator.
Für die Zeitkonstante $\tau$ gilt: $\tau = R \cdot C$.
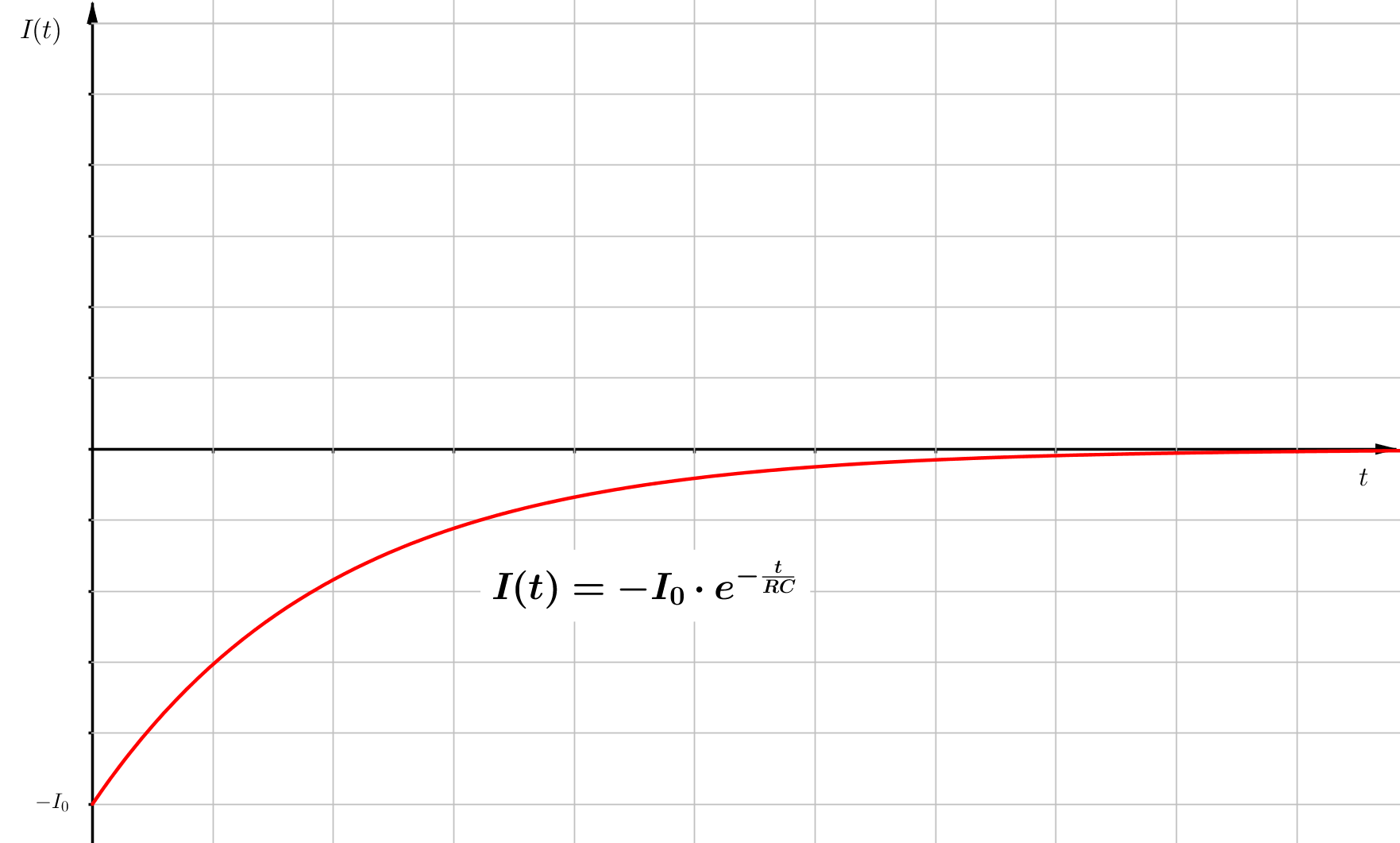
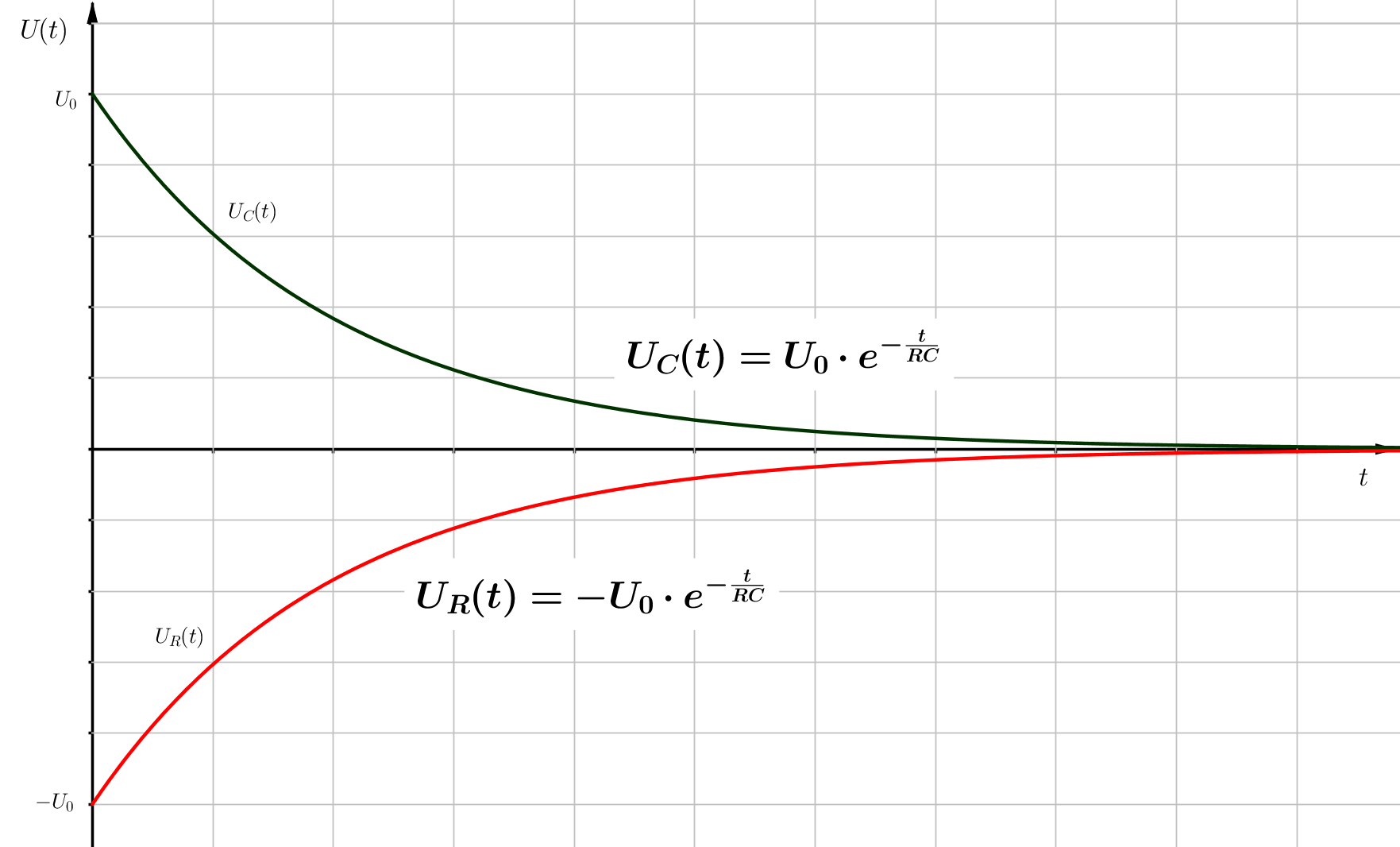
Für den Entladevorgang muss die Speisespannung kurzgeschlossen werden. Dann entläd sich der Kondensator mit einem Strom, der entgegen der Ladestromrichtung fließt. Für die Entladung gilt also die folgende Dgl. und die dazugehörende Anfangsbedingung: \begin{align} 0 &= R \cdot \frac{\Delta Q}{\Delta t} + \frac{Q}{C} \\ \\ Q(t = 0) &= Q_0 \end{align} Als Lösung ergibt sich die Funktion $Q(t)$ mit \begin{align} Q(t) = Q_0 \cdot e^{- \frac{t}{RC}} \end{align} Daraus folgen die Funktionsgleichungen für die Stromstärke $I(t)$, für die Kondensatorspannung $U_C$ und für die Spannung über dem Widerstand $U_R$: \begin{align} I(t) &= - I_0 \cdot e^{- \frac{t}{RC}} \\ \\ U_C(t) &= U_0 \cdot e^{- \frac{t}{RC}} \\ \\ U_R(t) &= - U_0 \cdot e^{- \frac{t}{RC}} \end{align}
© mondbrand MMXIX