Der Millikan-Versuch
Mit dem Öltröpfchen-Versuch schaffte es Robert Millikan 1910, den Betrag der Elementarladung zu berechnen. Er erhielt 1923 für seine
Leistung den Physik-Nobelpreis.
Für die Durchführung des Versuchs existieren verschiedene Messmethoden. Hier soll die Schwebemethode erläutert werden.
Der prinzipielle Versuchsaufbau
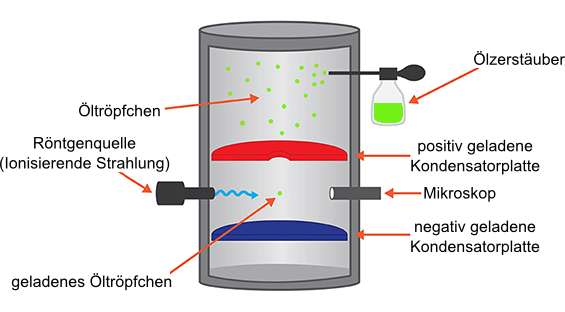Der Aufbau besteht aus einer Kammer, in der sich eine Plattenkondensatoranordnung befindet. Über der oberen Kondensatorplatte befindet sich ein
freier Bereich.
Mit Hilfe eines Zerstäubers wird Öl in der Form kleiner Tröpfchen in diesen freien Bereich gesprüht. Die Tröpfchen fallen nun durch ein kleines
Loch in der Mitte der oberen Kondensatorplatte und befinden sich jetzt zwischen den Kondensatorplatten. Durch die Bewegung der Öltröpfchen entsteht
auch Reibung, die dazu führt, dass die Tröpfchen eine unbestimmte Anzahl von Ladungen enthalten.
In einer anderen Versuchsanordnung wird der Bereich, durch den die Tröpfchen fallen, mit Röntgenstrahlung bestrahlt. Dadurch wird die Luft ionisiert
und die entstandenen freien Ladungen werden durch die Öltröpfchen in unterschiedlicher Anzahl aufgenommen.
Der Bereich zwischen den Kondensatorplatten kann von außen beobachtet werden.
Die Schwebemethode
Es müssen zwei Messungen durchgeführt werden. In einer ersten Messung wird bei einer bestimmten Spannung zwischen den Kondensatorplatten ein
Schwebezustand eines Öltröpfchens eingestellt. Diese Spannung wird notiert.
Die zweite Messung ist notwendig, weil das erste Messergebnis von dem Radius der Öltröpfchen abhängt, der ohne weiteres nicht zu messen ist. Bei der
zweiten Messung wird die Spannung zwischen den Kondensatorplatten auf Null gestellt und der Fall eines Öltröpfchens beobachtet. Dabei wird die
Geschwindigkeit bestimmt. Mit diesem Ansatz kann der Tröpfchenradius bestimmt werden.
Der Messansatz
Für den Schwebezustand gilt, dass sich die Gewichtskraft $F_G$ der Tröpfchen, die Coulombkraft $F_C$ des elektrischen Feldes und die Auftriebskraft $F_A$ der Tröpfchen
aufheben müssen.
\begin{align}
F_C &= F_G - F_A
\end{align}
Für die Coulombkraft gilt: $F_C = q \cdot E = q \cdot \frac {U}{d}$. Die Gewichtskraft lautet: $F_G = m \cdot g$. Die Masse eines Tröpfchens ist
gleich der Dichte des Öls multipliziert mit dem Volumen des Tröpfchens. Die Tröpfchen werden als Kugel angenommen, also gilt:
$m = \rho_Ö \cdot V_{Kugel} = \rho_Ö \cdot \frac{4}{3} \pi r^3$. Für die Auftriebskraft wird das von dem Öltröpfchen auf dem Weg nach oben verdrängte
Volumen betrachtet. Es gilt also: $F_A = m \cdot g = \rho_L \cdot V_{Kugel} \cdot g = \rho_L \cdot \frac{4}{3} \pi r^3 \cdot g$.
Insgesamt:
\begin{align}
q \cdot \frac{U}{d} &= \rho_Ö \cdot \frac{4}{3} \pi \cdot r^3 \cdot g - \rho_L \cdot \frac{4}{3} \pi \cdot r^3 \cdot g \\
q \cdot \frac{U}{d} &= \frac{4}{3} \pi \cdot r^3 \cdot g \cdot (\rho_Ö - \rho_L)
\end{align}
In der Gleichung bedeuten:
\begin{align}
U &: \text{Spannung am Kondensator} \\
d &: \text{Abstand der Kondensatorplatten} \\
\rho_Ö &: \text{Dichte des Öls} \\
\rho_L &: \text{Dichte der Luft} \\
r &: \text{Radius des Tröpfchens} \\
g &: \text{Ortsfaktor}
\end{align}
Umgestellt nach der Ladung erhält man:
\begin{align}
q = \frac {(\rho_Ö - \rho_L) \cdot \frac{4}{3} \pi \cdot g \cdot d \cdot r^3}{U}
\end{align}
Für die zweite Messung wird folgender Ansatz verwendet:
Das fallende Tröpfchen unterliegt der Gewichtskraft $F_G$, der Auftriebskraft $F_A$ an Luft und der sogenannten
Stokes-Reibung $F_R$, die geschwindigkeitsabhängig und als Reibkraft der Bewegung entgegengesetzt ist. Nach kurzer Zeit stellt sich eine
konstante Sinkgeschwindigkeit ein und es gilt:
\begin{align}
F_R + F_A &= F_G
\end{align}
Für die Stokes-Reibung gilt: $F_R = 6 \pi \cdot \eta \cdot r \cdot v$, wobei $\eta$ die Viskosität von Luft bezeichnet.
\begin{align}
6 \pi \cdot \eta \cdot r \cdot v + \rho_L \cdot \frac{4}{3} \pi \cdot r^3 \cdot g &= \rho_Ö \cdot \frac{4}{3} \pi \cdot r^3 \cdot g
\end{align}
Die Gleichung wird nach $r$ umgestellt. Man erhält:
\begin{align}
r = \sqrt{\frac{9 \eta v}{2 g (\rho_Ö - \rho_L)}}
\end{align}
Die Geschwindigkeit des Tröpfchen ist also proportional zum Quadrat des Radiusses, da alle anderen Werte wie die Dichten von Luft und Öl sowie die
Viskosität von Luft als konstant angenommen werden.
Es wird die Zeit gemessen, die das Tröpfchen für einen bestimmten Weg benötigt. Damit hat man die Geschwindigkeit und auf indirektem Weg auch den
Radius.
Eingesetzt in die Gleichung für die Ladung erhält man: \begin{align} q = \frac{9 \pi d}{U} \sqrt{\frac{2 \eta^3 v^3}{g (\rho_Ö - \rho_L)}} \end{align} Die Werte für $U$ und $v$ werden in den zwei Messungen nacheinander ermittelt und in die Gleichung eingesetzt.
Die Auswertung
In den jeweiligen Messungspaaren kann jeweils nur ein Tröpfchen beobachtet werden. Es müssen also eine Vielzahl von Messungen durchgeführt werden, um ein Ergebnis zu erhalten, dass in etwa so aussehen kann:
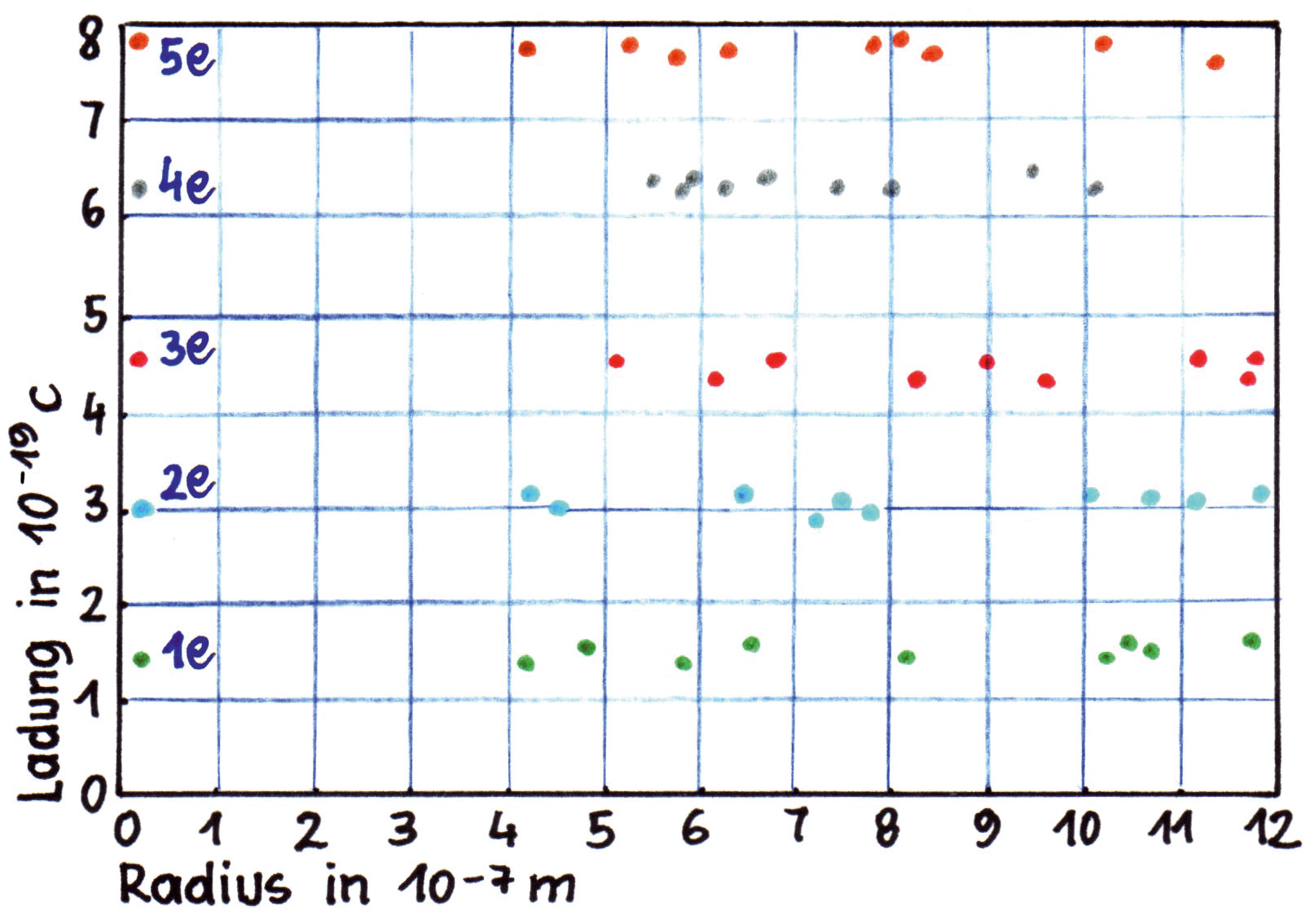
Quelle: https://www.oebv.at/system/files/celum/377624_23-09.jpg
Es ergibt sich, dass alle Messungen zu Ladungsmengen führen, die sich jeweils um einen Betrag unterscheiden, nämlich um den Betrag von $1,602 \cdot 10^{-19} \text{ C}$. Das wurde von Millikan so interpretiert, dass es eine kleinste Ladungsmenge, die sogenannte Elementarladung $e$, geben müsse.