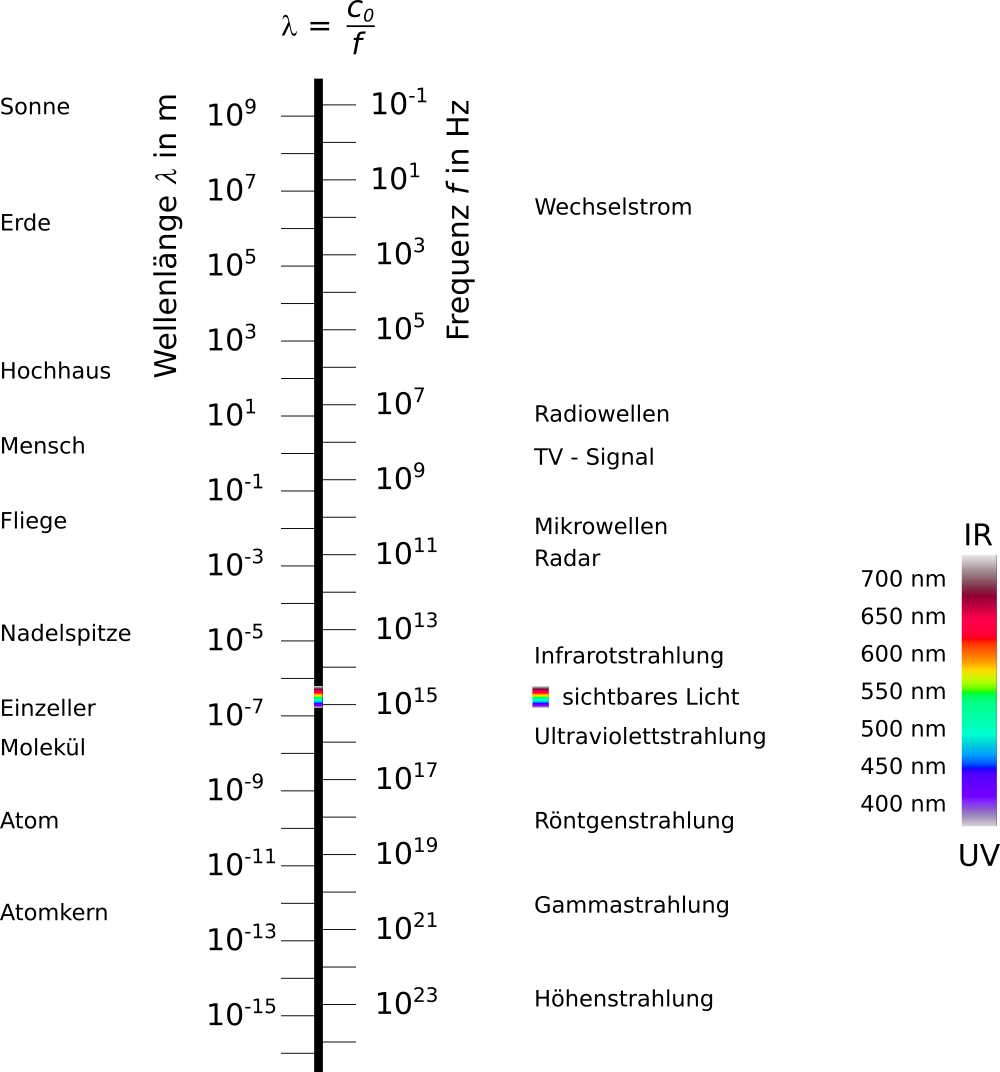Das elektromagnetische Spektrum
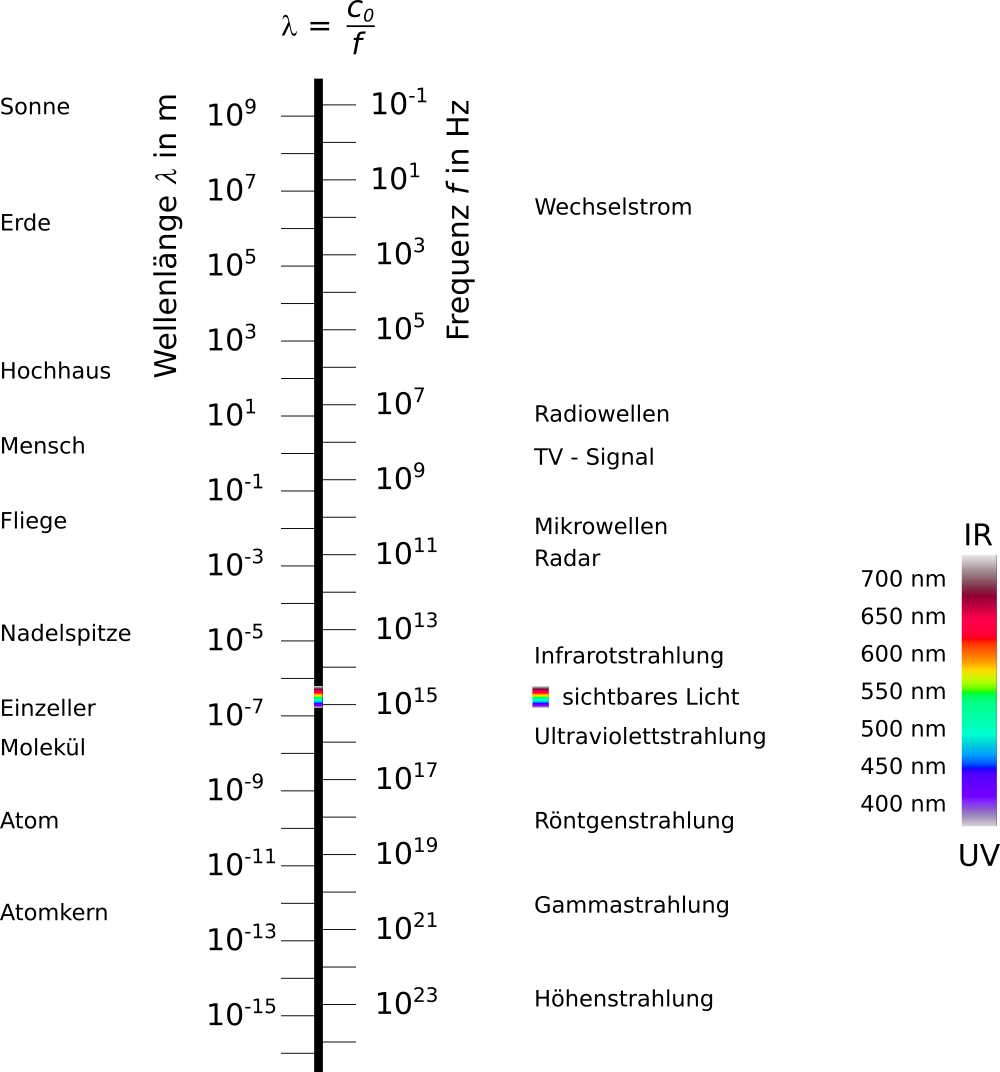
Die Frequenzbereiche und die Größenvergleiche der Wellenlängen sind nicht absolut zu sehen. In verschiedenen Quellen zum elektromagnetischen
Spektrum gibt es mehr oder weniger starke Unterschiede für die Frequenzbereiche der einzelnen Strahlungen.
Die einzelnen Bereiche
\begin{align}
& & \text{Wellen}&\text{länge} \qquad & \text{Fre}&\text{quenz} \\ \\
\text{Niederfrequenzbereich} &\qquad& 1 \cdot 10^5 \, \text{km} &- 10 \, \text{km} \qquad & 3 &- 3 \cdot 10^{4} \, \text{Hz} \\ \\
\text{Radiowellen} &\qquad& 10 \, \text{km} &- 300 \, \text{mm} \qquad & 3 \cdot 10^{4} &- 1 \cdot 10^{9} \, \text{Hz} \\ \\
\text{Mikrowellen} &\qquad& 300 \, \text{mm} &- 1 \, \text{mm} \qquad & 1 \cdot 10^{9} &- 3 \cdot 10^{11} \, \text{Hz} \\ \\
\text{Infrarotstrahlung} &\qquad& 1 \, \text{mm} &- 780 \, \text{nm} \qquad & 3 \cdot 10^{11} &- 4 \cdot 10^{14} \, \text{Hz} \\
\text{rotes Licht} &\qquad& 780 \, \text{nm} &- 650 \, \text{nm} \qquad & 4 \cdot 10^{14} &- 4,6 \cdot 10^{14} \, \text{Hz} \\
\text{oranges Licht} &\qquad& 650 \, \text{nm} &- 585 \, \text{nm} \qquad & 4,6 \cdot 10^{14} &- 5,1 \cdot 10^{14} \, \text{Hz} \\
\text{gelbes Licht} &\qquad& 585 \, \text{nm} &- 575 \, \text{nm} \qquad & 5,1 \cdot 10^{14} &- 5,2 \cdot 10^{14} \, \text{Hz} \\
\text{grünes Licht} &\qquad& 575 \, \text{nm} &- 490 \, \text{nm} \qquad & 5,2 \cdot 10^{14} &- 6,1 \cdot 10^{14} \, \text{Hz} \\
\text{blaues Licht} &\qquad& 490 \, \text{nm} &- 420 \, \text{nm} \qquad & 6,1 \cdot 10^{14} &- 7,1 \cdot 10^{14} \, \text{Hz} \\
\text{violettes Licht} &\qquad& 420 \, \text{nm} &- 380 \, \text{nm} \qquad & 7,1 \cdot 10^{14} &- 7,9 \cdot 10^{14} \, \text{Hz} \\
\text{Ultraviolettstrahlung} &\qquad& 380 \, \text{nm} &- 10 \, \text{nm} \qquad & 7,9 \cdot 10^{14} &- 3 \cdot 10^{16} \, \text{Hz} \\ \\
\text{Röntgenstrahlung} &\qquad& 10 \, \text{nm} &- 10 \, \text{pm} \qquad & 3 \cdot 10^{16} &- 3 \cdot 10^{19} \, \text{Hz} \\ \\
\text{Gammastrahlung} &\qquad& 10 \, \text{pm} &- 30 \, \text{fm} \qquad & 3 \cdot 10^{19} &- 1 \cdot 10^{22} \, \text{Hz} \\ \\
\text{Höhenstrahlung} &\qquad& 30 \, \text{fm} &- 1 \, \text{fm} \qquad & 1 \cdot 10^{22} &- 3 \cdot 10^{23} \, \text{Hz}
\end{align}