Die drei wesentlichen Aggregatzustände sind fest, flüssig und gasförmig. Sie unterscheiden sich im Allgemeinen dadurch, dass sie für jedes Material bei unterschiedlichen Temperaturen vorliegen. Der feste Zustand liegt bei einer niedrigeren Temperatur vor, der gasförmige Zustand bei einer höheren Temperatur. Dazwischen befindet sich der flüssige Zustand.
Daneben gibt es noch weitere Zustände von Materie, die als Aggregatzustand beschrieben werden können. Liegt das Material bereits in der Gasphase vor und die Temperatur wird weiter erhöht, können sich die Valenzelektronen, also die äußersten Elektronen der Atome von den Atomen lösen. Es entstehen positiv geladene Ionen und negativ geladene freie Elektronen. Diesen Zustand nennt man Plasma.
Wird feste Materie weiter abgekühlt, kann ein sogenanntes Bose-Einstein-Kondensat entstehen, was ebenfalls einen speziellen Materiezustand beschreibt. In diesem Kondensat verhalten sich alle Teilchen zusammen wie ein einziges Teilchen, was zu neuen Eigenschaften führt und deswegen als neuer Aggregatzustand bezeichnet wird.
In der folgenden Tabelle sind die Aggregatzustände zusammengefasst. Dazu werden die wesentlichen Eigenschaften, die sich mit Hilfe des Teilchenmodells erklären lassen, aufgelistet.
| Übersicht Aggregatzustände | ||
|---|---|---|
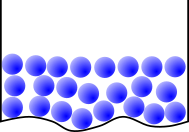
| fest (s) | flüssig (l) | gasförmig (g) |
 |
 |
 |
| Teilchen bilden den Körper | Teilchen nehmen die Unterseite der Gefäßform an und bilden oben eine ebene Oberfläche | jede Gefäßform wird gefüllt |
| konstantes Volumen (nicht komprimierbar) |
konstantes Volumen (nicht - oder nur sehr wenig - komprimierbar) |
Volumen ist druck- und temperaturabhängig (starke Komprimierbarkeit) |
| Teilchen sitzen auf Plätzen einer regelmäßigen gitterförmigen Struktur | keine regelmäßige Struktur, aber es gibt direkte Nachbarn | keine Struktur, keine Nachbarn |
| geringe Abstände zwischen den Teilchen | geringe Abstände zwischen den Teilchen | große Abstände zwischen den Teilchen |
| starke Kräfte zwischen den Teilchen | schwache Kräfte zwischen den Teilchen | keine Kräfte zwischen den Teilchen |
Im festen Zustand sind die Kräfte zwischen den Teilchen sehr groß. Die Kräfte werden durch die Bindungen symbolisiert, die als Federn
aufgefasst werden können. Federn können stark (große Federkonstante) oder schwach (kleine Federkonstante) sein und so starke
Bindungen und große Kräfte bzw. schwächere Bindungen und kleinere Kräfte darstellen. Die Federn erlauben kleine Bewegungen der
Teilchen um ihre eigentliche Gitterposition herum. Das führt dazu, dass die Teilchen keine großen Bewegungen ausführen können,
sondern nur kleine Schwingungsbewegungen um ihre Gleichgewichtsposition.
Wenn die Temperatur auf ihrem absoluten Nullpunkt ist $\left( T = 0 \text{ K} \right)$, liegen immer noch die sogenannten Nullpunktsbewegungen vor. Mit steigender Temperatur werden die Bewegungen immer stärker. Ab einer bestimmten Temperatur, die abhängig ist vom Material, kann es dazu kommen, dass eine Bewegung so stark ist, dass die Bindung abreisst. Geschieht das mehrfach und an unterschiedlichen Orten, spricht man davon, dass der Körper schmilzt. Es findet eine Umwandlung vom festen in den flüssigen Zustand statt.
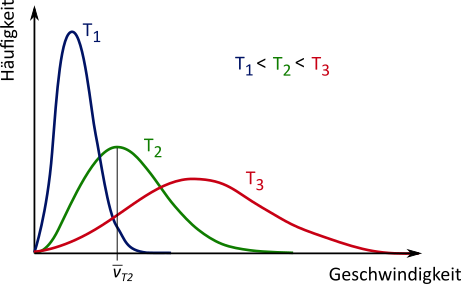
In einem Wassertropfen bewegen sich die Wasserteilchen mit einer mittleren Geschwindigkeit $\overline v$ unkontrolliert in alle möglichen
Richtungen. Wenige Teilchen bewegen sich mit einer wesentlich geringeren Geschwindigkeit, wenige mit einer wesentlich höheren Geschwindigkeit,
die meisten mit der mittleren Geschwindigkeit. Die Verteilung der Geschwindigkeiten der Teilchen hängt von der Temperatur ab. In der Abbildung ist
beispielhaft dargestellt, wie die Verteilung bei unterschiedlichen Temperaturen aussehen kann.
Ist die Geschwindigkeit eines Teilchens ausreichend hoch, reicht die Bewegungsenergie dieses Teilchens aus, um von der flüssigen in die gasförmige Phase zu wechseln; das Teilchen verlässt den Tropfen. Die in dem Tropfen verbliebenen Teilchen besitzen nun eine etwas geringere mittlere Geschwindigkeit. Das bedeutet, der Tropfen kühlt ab.
Wegen des jetzt bestehenden Temperaturunterschieds zwischen dem Tropfen und seiner Umgebung bzw. seiner Unterlage kommt es zu einem Temperaturausgleich, so dass die Temperaturen wieder im Gleichgewicht sind. Die Temperatur des Tropfens ist leicht angestiegen, die der Umgebung/Unterlage ist leicht abgesunken. Die Geschwindigkeitsverteilung der Teilchen im Tropfen ist wieder wie am Anfang und der Prozess kann mit einem anderen Teilchen wieder beginnen.
Durch den Temperaturausgleich zwischen Tropfen und Umgebung/Unterlage kühlt die Umgebung/Unterlage ab. Das ist das Prinzip „Verdunstungskühlung“, zu dem auch das Schwitzen gehört.
Die ausreichende Geschwindigkeit der Teilchen für diesen Prozess ist die mittlere Geschwindigkeit bei der Siedetemperatur. Das bedeutet, dass einzelne Teilchen immer und bei jeder Temperatur eine Geschwindigkeit haben, die der mittleren Geschwindigkeit bei der Siedetemperatur entspricht. Der Verdunstungsprozess findet bei jeder Temperatur statt. Je höher die Temperatur dabei ist, desto größer ist der Anteil der Teilchen, die in die Gasphase übertreten können.
Teilchen, die sich an der Oberfläche des Tropfens bewegen, können leichter in die Gasphase übertreten als Teilchen, die sich im Inneren des Tropfens befinden. Die Größe der Oberfläche des Tropfens spielt für den Verdunstungsprozess eine wichtige Rolle. Je größer die Oberfläche, desto mehr Teilchen befinden sich am Rande des Tropfens und können ihn leichter verlassen. Damit wird der Verdunstungsprozess schneller erfolgen.
Der Unterschied zwischen der beschriebenen Verdunstung und der Verdampfung ist eigentlich nur sprachlicher Natur. Physikalisch handelt es sich um denselben Prozess. Man spricht von „Verdampfung“, wenn der Übertritt in die Gasphase bei der Siedetemperatur stattfindet, und von „Verdunstung“ bei jeder anderen Temperatur.
Vermischen sich zwei Phasen, können verschiedene Prozesse ablaufen. Zunächst können sich die beiden Phasen komplett miteinander vermischen. Im Endergebnis würde man keine der beiden ursprünglichen Phasen mehr erkennen. Man spricht in diesem Zusammenhang von einer vollkommenen Mischbarkeit der Phasen. Wird z.B. Tinte in Wasser getropft, vermischen sich beide Flüssigkeiten vollständig. Nachdem der Prozess abgeschlossen ist, gibt es kein reines Wasser und keine reine Tinte mehr; es existiert nur noch das Wasser-Tinte-Gemisch (Mischphase). Es liegt also nur noch eine Phase vor.
Eine andere Möglichkeit ist die vollständige Nicht-Mischbarkeit zweier Phasen. Im Falle von zwei Flüssigkeiten kann als Beispiel die Vermischung von Wasser und Öl dienen. Diese beiden Flüssigkeiten vermischen sich praktisch gar nicht, so dass bei Abschluss des Prozesses immer reines Wasser und reines Öl vorliegen (Phasengemisch). Hier liegen zwei Phasen vor.
Dazwischen gibt es alle möglichen Kombinationen von Mischbarkeit (Phasengemisch aus Mischphasen). Im Allgemeinen liegen bei zwei Flüssigkeiten drei Phasen vor, nämlich die reine Flüssigkeit 1, die reine Flüssigkeit 2 und die Mischphase aus beiden Flüssigkeiten.
Diese prinzipiellen Überlegungen gelten für alle möglichen Phasenvermischungen, auch von Phasen in unterschiedlichen Aggregatzuständen.
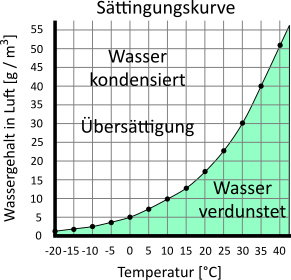
Ist ein Wasserteilchen aus einem Tropfen in die Gasphase übergetreten, wird das Teilchen seine Bewegungsenergie wieder abgeben und damit abkühlen. Somit müsste es also wieder in die flüssige Phase wechseln, also in der Luft kondensieren, und als Tropfen herabfallen. Die Luft als Phasengemisch hat allerdings die Fähigkeit, eine bestimmte Menge an flüssigem Wasser aufzunehmen, d.h. es gibt eine gewisse Mischbarkeit von gasförmiger Luft und flüssigem Wasser („Sättigung“). Diese Mischbarkeit ist temperaturabhängig und nimmt mit steigender Temperatur zu. Sie kann aus der Sättigungskurve entnommen werden.
Bei einer Temperatur von 10 °C etwa kann die Luft pro Kubikmeter (m3) 10 g Wasser aufnehmen.
Die relative Luftfeuchtigkeit, die in Hygrometern gemessen wird, ist das Verhältnis der tatsächlichen Feuchtigkeitsmenge zur Sättigungsfeuchtigkeit bei der entsprechenden Temperatur.
Beträgt bei einer Temperatur von 10 °C die tatsächliche Feuchtigkeitsmenge z.B. 5 g, dann führt das zu einer Luftfeuchtigkeit von 5 g / 10 g = 0,5, also 50%.
Befindet sich also viel Feuchtigkeit in der Luft (hohe relative Luftfeuchtigkeit), kann diese kaum noch weitere Feuchtigkeit aufnehmen. Der Verdunstungsprozess wird langsamer und kommt bei einer relativen Luftfeuchtigkeit von 100 % zum Erliegen. In diesem Fall wird das Wasser, was für die vorliegende Temperatur zu viel in der Luft ist, wieder kondensieren. Es entsteht z.B. Nebel oder Spiegeloberflächen beschlagen.
Um einen Stoff zu erwärmen, muss ihm Energie zugeführt werden. Die Energiemenge, die notwendig ist, um ein Kilogramm des Stoffes um
einen Grad Celsius zu erwärmen, wird spezifische Wärmekapazität c genannt. Die Einheit dieser Größe ist
$$
[ c ] = 1 \; \frac{\text{J}}{\text{kg}\cdot \text{K}}
$$
Die spezifische Wärmekapazität gilt ausschließlich nur für einen Aggregatzustand eines Stoffes. Dabei ist dann $c_s$ die
Bezeichnung für den festen Aggregatzustand (s: solid), $c_l$ für den flüssigen Zustand (l: liquid) und $c_g$ für den
gasförmigen Zustand (g: gaseous).
In den allermeisten Fällen gilt der Wert auch nur in einem sehr schmalen Temperaturbereich, da die spezifische
Wärmekapazität im Allgemeinen temperaturabhängig ist. In guter Näherung kann aber oft ein mittlerer Wert angenommen werden.
Für Wasser sind z.B. diese Werte tabelliert:
\begin{align} c_s &= 2060 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \\ \\ c_l &= 4186 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \\ \\ c_g &= 1870 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \end{align}Eine Liste verschiedener spezifischer Wärmekapazitäten gibt es z.B. hier
Für die Berechnung der zur Erwärmung benötigten Energiemenge $Q$ gilt:
$$ Q = c \cdot m \cdot \Delta T $$Dabei ist $c$ die spezifische Wärmekapazität des zu erwärmenden Stoffes, $m$ dessen Masse und $\Delta T$ die Temperaturdifferenz bei der Erwärmung. Für die Temperaturdifferenz gilt, dass $\Delta T$ in der Einheit Kelvin (K) gleich ist der Temperaturdifferenz $\Delta \theta$ in der Einheit Grad Celsius (°C).
Ein anderer wichtiger Energiewert betrifft nicht die Erwärmung oder Abkühlung eines Stoffes, sondern dessen Änderung des Aggregatzustands. Die Prozesse betreffen den Übergang von fest auf flüssig (und umgekehrt) sowie von flüssig auf gasförmig (und umgekehrt).
Die benötigte Energie, die den Übergang fest ➜ flüssig möglich macht, wird Schmelzwärme genannt. Der Übergang flüssig ➜ gasförmig wird durch die Verdampfungswärme möglich.
Alle Energien werden im Falle der Temperaturabsenkung frei, bei der Erwärmung muss sie hinzugefügt werden.
Die Schmelz- und die Verdampfungswärme wird mit $C$ bezeichnet. Dabei ist $$ C_S: \text{ Schmelzwärme} \\ C_V: \text{ Verdampfungswärme} $$ Die Einheit dieser Größe ist $$ [ C ] = 1 \; \frac{\text{J}}{\text{kg}} $$
Für Wasser sind die folgenden Werte tabelliert:
\begin{align} C_S &= 333,5 \; \frac{\text{kJ}}{\text{kg}} \\ \\ C_V &= 2257 \; \frac{\text{kJ}}{\text{kg}} \\ \\ \end{align}Für die Berechnung der benötigten Energiemenge $Q$ für den Übergang zwischen den Aggregetzuständen:
$$ Q = C \cdot m $$Dabei ist $C$ die Schmelz- bzw- Verdampfungswärme und $m$ die Masse des Stoffes.
Am Beispiel für Wasser soll der Energiebedarf bei verschiedenen Prozessen durchgerechnet werden.
1) 500 g Eis wird von -10 °C auf 15 °C erwärmt.
Für die Berechnung muss zuerst die Erwärmung des Eises auf die Schmelztemperatur berücksichtigt werden, dann die Zustandsänderung von fest auf flüssig, dann die weitere Erwärmung der Flüssigkeit auf die Endtemperatur. Es folgt also:
\begin{align} Q &= Q_1 + Q_2 + Q_3 \\ \\ Q_1 &= c_s \cdot m \cdot \Delta T \\ Q_1 &= 2060 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \cdot 0,5 \text{ kg} \cdot 10 \text{ K} \\ Q_1 &= 10300 \text{ J} \\ \\ Q_2 &= C_S \cdot m \\ Q_2 &= 333500 \; \frac{\text{J}}{\text{kg}} \cdot 0,5 \text{ kg} \\ Q_2 &= 166750 \text{ J} \\ \\ Q_3 &= c_l \cdot m \cdot \Delta T \\ Q_3 &= 4186 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \cdot 0,5 \text{ kg} \cdot 15 \text{ K} \\ Q_3 &= 31395 \text{ J} \\ \\ Q &= 10300 \text{ J} + 166750 \text{ J} + 31395 \text{ J} \\ Q &= 208445 \text{ J} \end{align}2) 2 l Wasser werden von 20 °C auf 95 °C erwärmt.
\begin{align} Q &= c_l \cdot m \cdot \Delta T \\ Q &= 4186 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \cdot 2 \text{ kg} \cdot 75 \text{ K} \\ Q_3 &= 627900 \text{ J} \end{align}3) 10 g Eis wird von -5 °C auf 110 °C erwärmt.
\begin{align} Q &= Q_1 + Q_2 + Q_3 + Q_4 + Q_5 \\ \\ Q_1 &= c_s \cdot m \cdot \Delta T \\ Q_1 &= 2060 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \cdot 0,01 \text{ kg} \cdot 5 \text{ K} \\ Q_1 &= 103 \text{ J} \\ \\ Q_2 &= C_S \cdot m \\ Q_2 &= 333500 \; \frac{\text{J}}{\text{kg}} \cdot 0,01 \text{ kg} \\ Q_2 &= 3335 \text{ J} \\ \\ Q_3 &= c_l \cdot m \cdot \Delta T \\ Q_3 &= 4186 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \cdot 0,01 \text{ kg} \cdot 100 \text{ K} \\ Q_3 &= 4186 \text{ J} \\ \\ Q_4 &= C_V \cdot m \\ Q_4 &= 2257000 \; \frac{\text{J}}{\text{kg}} \cdot 0,01 \text{ kg} \\ Q_4 &= 22570 \text{ J} \\ \\ Q_5 &= c_g \cdot m \cdot \Delta T \\ Q_5 &= 1870 \; \frac{\text{J}}{\text{kg} \cdot \text{K}} \cdot 0,01 \text{ kg} \cdot 10 \text{ K} \\ Q_5 &= 187 \text{ J} \\ \\ Q &= 103 \text{ J} + 3335 \text{ J} + 4186 \text{ J} + 22570 \text{ J} + 187 \text{ J} \\ Q &= 30381 \text{ J} \end{align}Wird der Prozess als Diagramm dargestellt, ergibt sich im Allgemeinen folgendes:
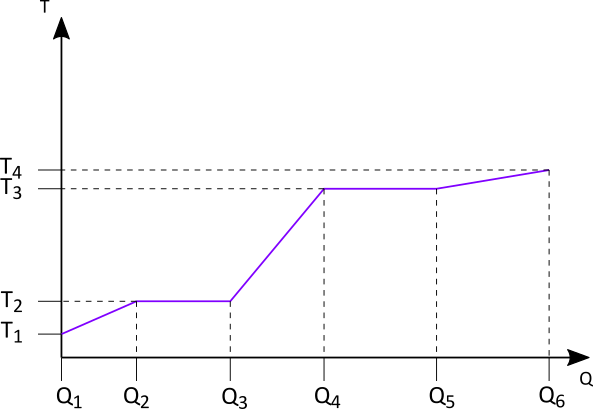
Der erste Prozess zeigt die Erhöhung der Temperatur von $T_1$ auf $T_2$ an. Dafür wird ein Energie- bzw. Wärmebetrag von $Q = Q_2 - Q_1$ benötigt.
Beim zweiten Prozess wird eine Energiemenge $Q = Q_3 - Q_2$ zugeführt, was zur Änderung des Aggregatzustands von fest auf flüssig führt. Es findet in dieser Phase keine Temperaturerhöhung statt. In diesem allgemeinen Beispiel wäre $T_2$ gleich der Schmelztemperatur des Stoffes.
Im dritten Prozess findet wieder eine Temperaturerhöhung von $T_2$ nach $T_3$ statt. Die dafür benötigte Energiemenge beträgt $Q = Q_4 - Q_3$.
Der Übergang von der flüssigen in die gasförmige Phase findet beim vierten Prozess statt. Bei konstanter Temperatur $T_3$, hier der Siedetemperatur, wird die Energiemenge $Q = Q_5 - Q_4$ benötigt.
Im fünften Prozess schließlich wird mit der Energiemenge $Q = Q_6 - Q_5$ die Temperatur von $T_3$ auf $T_4$ erhöht.
Die Steigungen im $Q-T-$Diagramm entsprechen dem Kehrwert der spezifischen Wärmekapazität $\left( \frac{1}{c \cdot m} \right)$. Denn aus $Q = c \cdot m \cdot \Delta T$ folgt $\Delta T = \frac{Q}{c \cdot m}$.
Die Bereiche konstanter Temperatur zeigen an, dass die zugeführte Energie für die Änderung des Aggregatzustands genutzt wird und nicht für die Erhöhung der Temperatur.
© mondbrand MMXIX