

Als geradlinige Bewegungen werden diejenigen Bewegungen bezeichnet, deren Weg eine bestimmbare Länge besitzen, z.B. weil der Weg eine geometrische Figur beschreibt oder weil eine mathematische Funktion dahintersteht.
 Die Bewegung der Erde um die Sonne ist eine Bewegung auf einer Kreisbahn. Diese Kreisbahn hat aber eine ganz bestimmte
Länge, in diesem Fall den Umfang eines Kreises mit dem Abstand der Erde von der Sonne als Radius, r = 150000000 km. Für den Umfang
gilt dann:
$$
U = 2 \cdot \pi \cdot r
$$
In diesem Beispiel wäre also die Länge des Weges, den die Erde im Laufe eines Jahres zurücklegt:
$$
U = 9,4 \cdot 10^8 \; \text{km}
$$
Die Bewegung der Erde um die Sonne ist eine Bewegung auf einer Kreisbahn. Diese Kreisbahn hat aber eine ganz bestimmte
Länge, in diesem Fall den Umfang eines Kreises mit dem Abstand der Erde von der Sonne als Radius, r = 150000000 km. Für den Umfang
gilt dann:
$$
U = 2 \cdot \pi \cdot r
$$
In diesem Beispiel wäre also die Länge des Weges, den die Erde im Laufe eines Jahres zurücklegt:
$$
U = 9,4 \cdot 10^8 \; \text{km}
$$
Der Begriff geradlinig ist also nicht wörtlich zu verstehen.
Der Weg, auf dem eine Bewegung stattfindet, wird i.A. mit dem Buchstaben $s$ bezeichnet. Die Standardeinheit für den Weg ist Meter. $$ \text{Strecke} \; s \\ [s] = 1 \; \text{m} $$ Für die Zeitspanne, die eine Bewegung andauert, wird der Buchstabe $t$ verwendet, mit der Einheit Sekunde. $$ \text{Zeit} \; t \\ [t] = 1 \; \text{s} $$
 Für die Beschreibung einer Bewegung ist es notwendig, die Veränderung der Position eines Objektes auf einer Strecke in
Abhängigkeit von der Zeit zu wissen.
Für die Beschreibung einer Bewegung ist es notwendig, die Veränderung der Position eines Objektes auf einer Strecke in
Abhängigkeit von der Zeit zu wissen.
Für die Veränderung der Position schreibt man $\Delta s$ und für die dafür benötigte Zeitspanne $\Delta t$. Der
Quotient aus den beiden Größen nennt man Geschwindigkeit $v$. Es gilt:
$$
v = \frac{\Delta s}{\Delta t} = \frac{s_1 - s_0}{t_1 - t_0}
$$
Die Größen $s_0$ und $t_0$ sind dabei immer die Größen am Anfang einer Messung. Die weiteren Größen, die im
Verlauf der Bewegung noch bestimmt werden, werden dann folgerichtig mit $s_1, t_1, s_2, t_2, $ usw. bezeichnet.
Im Gegensatz dazu bezeichnen die Größen $s$ und $t$ Variablen, d.h. unbekannte und veränderliche Größen.
Für die Geschwindigkeit $v$ erhält man die Einheit Meter pro Sekunde: $$ \text{Geschwindigkeit} \; v\\ [v]=1 \; \frac{\text{m}}{\text{s}}$$
Stellt man $v = \frac{\Delta s}{\Delta t}$ nach $\Delta s$ um, erhält man das Zeit-Weg-Gesetz: $$ \Delta s = v \cdot \Delta t $$
Die Strecke $s$ und die Zeit $t$ sind also proportional zueinander. Der Proportionalitätsfaktor ist dann die Geschwindigkeit $v$.
In manchen Fällen ist es sinnvoll, die zu beschreibende Bewegung als Diagramm darzustellen. Hier ist es üblich, auf der
$x-$Achse die Zeit $t$ aufzutragen und auf der $y-$Achse die Strecke $s$. Damit erhält man ein $t-s-$Diagramm:


Links ist der proportionale Verlauf der Strecke in Abhängigkeit von der Zeit zu sehen. Die Steigung der Geraden ist die
Geschwindigkeit, die somit auch mit Hilfe des Steigungsdreiecks ermittelt werden kann.
Rechts ist die Gerade um $s_0$ nach oben verschoben. Die Steigung und damit die Geschwindigkeit ist dieselbe wie in der linken
Abbildung.
Proportional bedeutet, dass die Gerade durch den Koordinatenursprung verlaufen muss. Daher ist in diesem Fall $s_0 = 0$ und $t_0 = 0$. So entsteht aus \begin{align} \Delta s &= v \cdot \Delta t \\ \left( s_1 - s_0 \right) & = v \cdot \left( t_1 - t_0 \right) \\ s_1 & = v \cdot t_1 \\ s(t) & = v \cdot t \end{align}
In der rechten Abbildung ist $s_0 \neq 0$, daher folgt aus $ \Delta s = v \cdot \Delta t$: \begin{align} \left( s_1 - s_0 \right) & = v \cdot \left( t_1 - t_0 \right) \\ s_1 & = v \cdot t_1 + s_0 \\ s(t) & = v \cdot t + s_0 \end{align}
 Eine andere Form der Darstellung ist das $t-v-$Diagramm. Hier wird auf der $y-$Achse die Geschwindigkeit $v$ aufgetragen.
Eine andere Form der Darstellung ist das $t-v-$Diagramm. Hier wird auf der $y-$Achse die Geschwindigkeit $v$ aufgetragen.
Das in der Abbildung markierte Viereck hat die Kantenlängen $a = v_1$ und $b = t_2 - t_1 = \Delta t$. Der Flächeninhalt des
Viereckes ist demnach $A = a \cdot b = v_1 \cdot \Delta t$. Das wiederum ist gleich der Strecke $s = v_1 \cdot \Delta t$.
In einem $t-v-$Diagramm kann man also die mit einer Geschwindigkeit $v$ zurückgelegten Strecke $s$ bestimmen, indem man
die Fläche unter der Geraden in dem betrachteten Zeitintervall $\Delta t$ berechnet.
Der Fall $s_0 \neq 0$ muss allerdings extra berücksichtigt werden, da der Fall im $t-v-$Diagramm nicht zu erkennen ist.
Im $t-v-$Diagramm wird deutlich, dass sich die Geschwindigkeit der Bewegung im Verlauf der Zeit nicht verändert. Man hat also eine konstante Geschwindigkeit. Ist das bei einer Bewegung der Fall, spricht man von einer gleichförmigen Bewegung.
In diesem Abschnitt sollen Ansätze für die Bearbeitung verschiedener Aufgaben aus dem Bereich der gleichförmigen Bewegungen gezeigt werden. Dabei soll bitte beachtet werden, dass es jeweils nur eine von mehreren Möglichkeiten ist, die entsprechende Aufgabe zu lösen. Andere Wege oder andere Ansätze sind auch (fast) immer möglich.
• Einfache Bewegung
Ein Radfahrer fährt mit einer konstanten Geschwindigkeit von A-dorf nach B-stedt. Beide Orte liegen 12 km voneinander entfernt. Der Radfahrer benötigt 45 Minuten für die Fahrt.
Berechne die durchschnittliche Geschwindigkeit des Radfahrers.
Es gilt:
\begin{align} v &= \frac{\Delta s}{\Delta t} \\ \\ v &= \frac{12 \text{ km}}{45 \text{ min}} \\ \\ v &= \frac{12 \text{ km}}{0,75 \text{ h}} \\ \\ v &= 16 \; \frac{\text{km}}{\text{h}} \end{align}Zu beachten ist hier auf jeden Fall, dass die Einheiten richtig eingesetzt werden. Eine Geschwindigkeitseinheit km/min ist zwar möglich und nicht falsch, aber unüblich. Die Einheit km/h ist üblich und für solche Bewegungsaufgaben, d.h. Aufgaben, in denen alltägliche Bewegungen beschrieben werden sollen, auch angemessen. Die eigentlich richtige Einheit ist allerdings m/s und würde in dem Beispiel noch eine Umrechnung erfordern $\left( v = 4,44 \; \frac{\text{m}}{\text{s}}\right)$
• Zwei Bewegungen in dieselbe Richtung
Ein 100 m-Läufer startet bei $t = 0 \text{ s}$ und läuft mit einer durchschnittlichen Geschwindigkeit von $v = 8 \; \frac{\text{m}}{\text{s}}$. Ein zweiter Läufer startet etwas später, nämlich bei $t = 2 \text { s}$ und läuft durchschnittlich mit $v = 10 \; \frac{\text{m}}{\text{s}}$.
Wer erreicht das Ziel zuerst?
Eine solche Aufgabe lässt sich oft mit dem $t - s-$Diagramm lösen.
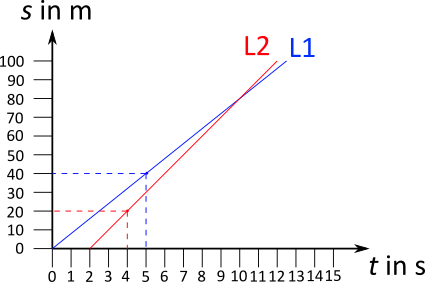
Zur Erstellung des Diagramms ist es sinnvoll, sich Punkte zu überlegen, die einfach in das Diagramm eingetragen werden können. Für den ersten Läufer ist das neben dem Punkt im Ursprung (Start bei t = 0 s) der Punkt bei 5 s und 40 m, denn 8 m/s bedeutet 16 m in 2 s und eben auch 40 m in 5 s. Bei dem zweiten Läufer kann man aus 10 m/s ganz einfach 100 m in 10 s machen. Zusammen mit dem um zwei Sekunden späteren Start ergibt das den Punkt 12 s und 100 m oder, wie im Diagramm markiert, 4 s und 20 m.
Die Frage, wer das Ziel zuerst erreicht, kann so sehr einfach beantwortet werden: Es ist Läufer Zwei.
Sollte die Frage jedoch lauten, wann und wo Läufer Zwei Läufer Eins überholt, d.h. wo sich der Schnittpunkt der beiden Geraden befindet, reicht das Diagramm u.U. nicht aus, da die Genauigkeit fehlt.
In einem solchen Fall bietet es sich an, mit dem Zeit-Weg-Gesetz zu arbeiten.
Es gilt:
\begin{align} s_1(t) &= 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 \\ s_2 (t) &= 10 \; \frac{\text{m}}{\text{s}} \cdot t_2 \end{align}$s_1$ und $s_2$ sind gleich: $s_1 = s_2 = s$. Für die Zeit $t_2$ gilt: $t_1 - 2 \text{ s}$, da Läufer 2 zwei Sekunden später startet. Es folgen die beiden Gleichungen:
\begin{align} s &= 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 \\ s &= 10 \; \frac{\text{m}}{\text{s}} \cdot \left(t_1 - 2 \text{ s} \right) \end{align}Gleichsetzen liefert:
\begin{align} 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= 10 \; \frac{\text{m}}{\text{s}} \cdot \left(t_1 - 2 \text{ s} \right) \\ \\ 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= 10 \; \frac{\text{m}}{\text{s}} \cdot t_1 - 20 \text{ m} \\ 8 \; \frac{\text{m}}{\text{s}} \cdot t_1 - 10 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= - 20 \text{ m} \\ - 2 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= - 20 \text{ m} \\ 2 \; \frac{\text{m}}{\text{s}} \cdot t_1 &= 20 \text{ m} \\ t_1 &= \frac{20 \text{ m}}{2 \; \frac{\text{m}}{\text{s}}} \\ t_1 &= 10 \text{ s} \end{align}Mit der Information kann nun auch der Ort angegeben werden:
\begin{align} s_1 (10 \text{ s}) &= 8 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} \\ s_1 &= 80 \text{ m} \end{align}Läufer 1 wird also nach 10 s und 80 m von Läufer 2 überholt.
• Zwei Bewegungen in entgegengesetzter Richtung
Ein Auto fährt von Braunschweig ins 335 km entfernte Frankfurt am Main. Gleichzeitig fährt in Frankfurt ein zweites Auto in Richtung Braunschweig los. Das erste Auto fährt mit durchschnittlich 75 km/h, das zweite mit durchschnittlich 60 km/h.
Wann und wo fahren sie aneinander vorbei?
Hier ist zunächst eine Skizze angebracht, um sich die Zeit-Weg-Gesetze beider Bewegungen klar zu machen.

Der Ursprung des Koordinatensystems liegt in Braunschweig. Für Auto EIns folgt also, dass es sich mit einer positiven Geschwindigkeit bewegt. Für Auto Zwei widerum folgt, dass es sich mit einer negativen Geschwindigkeit bewegt. Weiterhin muss die Bewegungsgerade für Auto Zwei um 335 km nach oben verschoben werden. Es folgen:
\begin{align} s_1 (t) &= 75 \; \frac{\text{km}}{\text{h}} \cdot t_1 \\ \\ s_2 (t) &= - 60 \; \frac{\text{km}}{\text{h}} \cdot t_2 + 335 \text{ km} \end{align}Für den Punkt der Vorbeifahrt beider Autos gilt, dass die Zeiten $t_1$ und $t_2$ identisch sein müssen. Weiterhin wird nun gefordert, dass genau zu dem Zeitpunkt $t_1 = t_2 = t$ auch der Ort gleich sein muss $(s_1 = s_2)$. Damit folgt:
\begin{align} 75 \; \frac{\text{km}}{\text{h}} \cdot t &= - 60 \; \frac{\text{km}}{\text{h}} \cdot t + 335 \text{ km} \\ 135 \; \frac{\text{km}}{\text{h}} \cdot t &= 335 \text{ km} \\ t &= \frac{335 \text{ km}}{135 \; \frac{\text{km}}{\text{h}}} \\ t &= 2,481 \text{ h} \\ \\ s_1 (2,481 \text{ h}) &= 75 \; \frac{\text{km}}{\text{h}} \cdot 2,481 \text{ h} \\ s_1 &= 186,1 \text{ km} \end{align}Die Vorbeifahrt findet somit nach ca. 2,5 Stunden 186 km von Braunschweig entfernt statt (Das ist etwa auf halber Strecke zwischen Kassel und dem Hattenbacher Dreieck, dem Übergang von der A7 auf die A5).
Verändert sich die Geschwindigkeit, spricht man von einer ungleichförmigen Bewegung. Für diesen Fall betrachtet man die Veränderung der Geschwindigkeit, analog zur Veränderung der Position bei den gleichförmigen Bewegungen: $$ a = \frac{\Delta v}{\Delta t} = \frac{v_1 - v_0}{t_1 - t_0} $$ Dabei wird die Beschleunigung $a$ definiert als die Veränderung der Geschwindigkeit in einem Zeitintervall. Dabei erhält man als Einheit für die Beschleunigung Meter pro Sekunde zum Quadrat. $$ \text{Beschleunigung} \; a \\ [a] = 1 \; \frac{\text{m}}{\text{s}^2} $$
 Ebenfall analog zu den oben genannten Fällen ergibt sich im $t-v-$Diagramm eine Gerade mit der Steigung $a$.
$$
\Delta v = a \cdot \Delta t
$$
$$
v_1 = a \cdot \Delta t + v_0
$$
Zusammen mit $t_0 = 0$ und $v_0 \neq 0$ ergibt sich:
$$
v(t)=a \cdot t+v_0
$$
Der zurückgelegte Weg $s$ wird ebenfalls berechnet, indem man die Fläche unter der Geraden berechnet:
$$
A = s = v_1 \cdot \Delta t + \frac{1}{2} \Delta v \cdot \Delta t
$$
Der Summand $v_1 \cdot \Delta t$ ist durch das lila Viereck gekennzeichnet, der Summand $\frac{1}{2} \Delta v \cdot \Delta t$
durch das blaue Dreieck.
Ebenfall analog zu den oben genannten Fällen ergibt sich im $t-v-$Diagramm eine Gerade mit der Steigung $a$.
$$
\Delta v = a \cdot \Delta t
$$
$$
v_1 = a \cdot \Delta t + v_0
$$
Zusammen mit $t_0 = 0$ und $v_0 \neq 0$ ergibt sich:
$$
v(t)=a \cdot t+v_0
$$
Der zurückgelegte Weg $s$ wird ebenfalls berechnet, indem man die Fläche unter der Geraden berechnet:
$$
A = s = v_1 \cdot \Delta t + \frac{1}{2} \Delta v \cdot \Delta t
$$
Der Summand $v_1 \cdot \Delta t$ ist durch das lila Viereck gekennzeichnet, der Summand $\frac{1}{2} \Delta v \cdot \Delta t$
durch das blaue Dreieck.
Wird nun noch das $\Delta v$ durch den Ausdruck $a \cdot \Delta t$ ersetzt, erhält man:
$$
\Delta s = v_1 \cdot \Delta t + \frac{1}{2} a \cdot \Delta t^2 \\
s_1 = \frac{1}{2} a \cdot \Delta t^2 + v_1 \cdot \Delta t + s_0
$$
Gilt nun noch, dass $t_0 = 0$ und $s_0 \neq 0$ ist, folgt:
$$
s(t) = \frac{1}{2} a \cdot t^2 + v_0 \cdot t + s_0 \\
v(t)= a \cdot t + v_0
$$
Mit diesen beiden Gleichungen lassen sich eigentlich alle Bewegungsaufgaben lösen, denn auch die gleichförmige Bewegung ist in ihnen enthalten. Bei der gleichförmigen Bewegung ist die Geschwindigkeit konstant, d.h. die Geschwindigkeitsänderung und damit die Beschleunigung ist Null. Damit entfällt der Term $\frac{1}{2}a \cdot t^2$ bzw. der Term $a \cdot t$.
Die ungleichförmigen Bewegungen werden auch nochmal unterteilt in den bis eben beschriebenen Fall der gleichmäßig beschleunigten Bewegung mit einer konstanten Beschleunigung $a$ und den Fall der ungleichmäßig beschleunigten Bewegung, bei der auch die Beschleunigung zeitabhängig ist, also $a(t)$ gilt.
• Einfache beschleunigte Bewegung - 1
Ein Fahrzeug wird in fünf Sekunden von 0 auf 100 km/h beschleunigt.
Bestimme die Beschleunigung.
Es gilt der Zusammenhang
\begin{align} a &= \frac{\Delta v}{\Delta t} \\ \\ a &= \frac{v_1 - v_0}{t_1 - t_0} \\ \\ a &= \frac{100 - 0 \; \frac{\text{km}}{\text{h}}}{5 \text{ s}} \\ \\ a &= \frac{100 \; \frac{\text{km}}{\text{h}}}{5 \text{ s}} \end{align}Die Geschwindigkeit muss in $\frac{m}{s}$ umgerechnet werden:
\begin{align} 100 \; \frac{\text{km}}{\text{h}} &= 100 \; \frac{1000 \text{ m}}{3600 \text{ s}} \\ &= 27,78 \; \frac{\text{m}}{\text{s}} \end{align}Es folgt:
\begin{align} a &= \frac{27,78 \; \frac{\text{m}}{\text{s}} }{5 \text{ s}} \\ \\ a &= 5,56 \; \frac{\text{m}}{\text{s}^2} \end{align}• Einfache beschleunigte Bewegung - 2
Ein Fahrzeug beschleunigt mit $a = 2 \; \frac{\text{m}}{\text{s}^2}$ auf einer Strecke von $s = 1200 \text{ m}$ aus dem Stillstand.
Berechne die Geschwindigkeit des Fahrzeugs am Ende der Beschleunigung.
Es gelten die Zusammenhänge:
\begin{align} s &= \frac12 a t^2 \\ v &= at \end{align}$v = at$ wird nach der Zeit umgestellt $(t = \frac{v}{a})$ und in die andere Gleichung eingesetzt.
\begin{align} s &= \frac12 a \left( \frac{v}{a} \right)^2 \\ \\ s &= \frac{v^2}{2a} \end{align}Gesucht ist die Geschwindigkeit, nach der die Gleichung umgestellt werden muss.
\begin{align} v &= \sqrt{2as} \\ \\ v &= \sqrt{2 \cdot 2 \; \frac{\text{m}}{\text{s}^2} \cdot 1200 \text{ m}} \\ \\ v &= 69,28 \; \frac{\text{m}}{\text{s}} \\ v &= 249,41 \; \frac{\text{km}}{\text{h}} \end{align}In diesem Zusammenhang wurden zwei weitere Gleichungen, die bei beschleunigten Bewegungen eine Rolle spielen können, entwickelt (plus eine dritte, die entsprechend durch Umstellung entsteht).
$$ s = \frac{v^2}{2a} \\ \\ v = \sqrt{2as} \\ \\ a = \frac{v^2}{2s} $$Wenn die Zeit bei der Bearbeitung der Aufgabe keine Rolle spielt, und nur die Größen $s$, $v$ und $a$ vorkommen, können diese neuen Zusammenhänge genutzt werden.
• Gleichförmige und beschleunigte Bewegung nacheinander
Ein Auto rollt 30 Sekunden mit konstant 54 km/h eine Straße entlang. Dann wird das Auto innerhalb von 10 Sekunden auf 72 km/h beschleunigt und fährt so noch weitere 20 Sekunden.
Wie weit ist das Auto insgesamt gekommen?
Zunächst sollte eine Skizze eines $t-v-$Diagramms angefertigt werden, um sich über den Ablauf im Klaren zu sein. Die Geschwindigkeiten $v = 54 \; \frac{\text{km}}{\text{h}} = 15 \; \frac{\text{m}}{\text{s}}$ sowie $v = 72 \; \frac{\text{km}}{\text{h}} = 20 \; \frac{\text{m}}{\text{s}}$ sollten umgerechnet werden. Die Alternative wäre eine Umrechnung der Zeiten, z.B. $t = 30 \text{ s} = 0,0083 \text{ h}$. Das wäre aber nicht sinnvoll.
Bei der Erstellung des Diagramms ist es wichtig, das die Einheiten der Größen, die als $x-$ bzw. $y-$Achse dienen, zusammenpassen, also z.B. $\frac{m}{s}$ und $s$ (wobei die Strecke in $m$ herauskommt) oder $\frac{km}{h}$ und $h$ (mit der Strecke in $km$). Wenig sinnvoll, aber möglich ist auch $\frac{\text{Lichtjahr}}{\text{Woche}}$ und $\text{Woche}$ mit der Strecke in $\text{Lichtjahren}$.
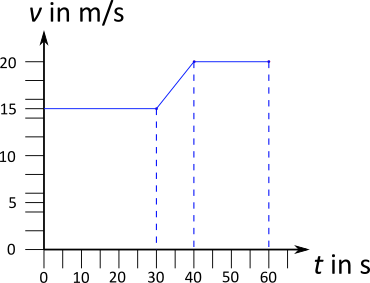
Aus der Fläche unter dem Graphen im $t-v-$Diagramm kann die zurückgelegte Strecke bestimmt werden. Dazu werden die unterschiedlichen Flächenstücke farbig markiert.
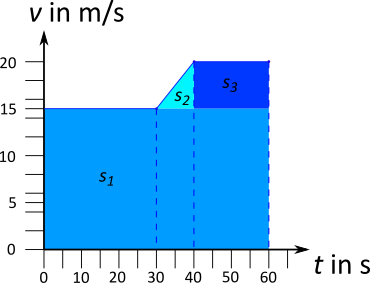
Für die einzelnen Flächen folgen die Flächeninhalte:
\begin{align} s_1 &= 15 \; \frac{\text{m}}{\text{s}} \cdot 60 \text{ s} \\ s_1 &= 900 \text{ m} \\ \\ s_2 &= \frac12 \cdot 5 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} \\ s_2 &= 25 \text{ m} \\ \\ s_3 &= 5 \; \frac{\text{m}}{\text{s}} \cdot 20 \text{ s} \\ s_3 &= 100 \text{ m} \\ \\ s &= s_1 + s_2 + s_3 \\ s &= 1025 \text{ m} \end{align}Ein alternative Betrachtung erfolgt, indem man die einzelnen Bewegungsabschnitte untersucht:
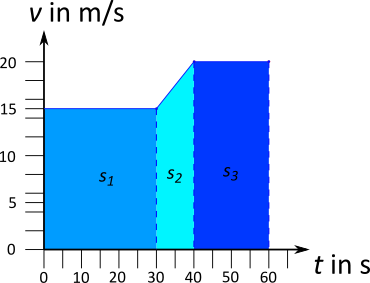
Für den ersten Abschnitt liegt eine gleichförmige Bewegung vor. Die zurückgelegte Strecke lässt sich mit dem folgenden Ansatz bestimmen:
\begin{align} s_1 &= v \cdot t \\ s_1 &= 15 \; \frac{\text{m}}{\text{s}} \cdot 30 \text{ s} \\ s_1 &= 450 \text{ m} \end{align}Der zweite Abschnitt beinhaltet eine beschleunigte Bewegung mit einer Anfangsgeschwindigkeit $v_0$:
\begin{align} s_2 &= \frac12 \cdot a \cdot t^2 + v_0 \cdot t \\ s_2 &= \frac12 \cdot \Delta v \cdot t + v_0 \cdot t \\ s_2 &= \frac12 \cdot 5 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} + 15 \; \frac{\text{m}}{\text{s}} \cdot 10 \text{ s} \\ s_2 &= 175 \text{ m} \end{align}Im dritten Abschnitt liegt wieder eine gleichförmige Bewegung vor:
\begin{align} s_1 &= v \cdot t \\ s_1 &= 20 \; \frac{\text{m}}{\text{s}} \cdot 20 \text{ s} \\ s_1 &= 400 \text{ m} \end{align}Insgesamt wird damit der Weg $s = s_1 + s_2 + s_3 = 1025 \text{ m}$ zurückgelegt.
• Gleichförmige und (mehrere) beschleunigte Bewegung(-en) gleichzeitig
Liegen gleichzeitig mehrere Bewegungszustände vor, u.U. auch mehrere Bewegungszustände der gleichen Art, können alle Zustände einzeln betrachtet werden. Sie überlagern sich ungestört (Superpositionsprinzip).
Eine Kugel rollt auf einer leicht abwärts geneigten Rollbahn. Sie bewegt sich anfangs mit einer konstanten Geschwindigkeit $v_0 = 1,5 \, \frac{\text{m}}{\text{s}}$. Durch die Neigung erfährt sie eine Beschleunigung von $a_1 = 0,5 \; \frac{\text{m}}{\text{s}^2}$. Weil sie aber auf einer Rollbahn rollt, wird sie auch durch die Reibung gebremst. Das wird durch eine zweite Beschleunigung $a_2 = -0,3 \; \frac{\text{m}}{\text{s}^2}$ ausgedrückt. Die Bahn hat insgesamt eine Länge von $s = 3 \text{ m}$, die Kugel startet mit der Anfangsgeschwindigkeit $v_0$ bei $t_0 = 0 \text{ s}$ und $s_0 = 0 \text{ m}$.
Bestimme die zurückgelegte Strecke nach $t_1 = 1,2 \text{ s}$.
Zu welchem Zeitpunkt hat die Kugel das Ende der Rollbahn erreicht?
Bestimme die Geschwindigkeit der Kugel bei $s_1 = 1,5 \text{ m}$ und am Ende der Bahn.
Es gilt der Zusammenhang
$$ s = \frac12 a t^2 + v_0 t + s_0 $$Für die gegebene Aufgabenstellung lautet der Ansatz:
\begin{align} s(t_1) &= \frac12 \cdot a_1 \cdot t_1^2 + \frac12 \cdot a_2 \cdot t_1^2 + v_0 \cdot t_1 \end{align}Da alle Bewegungen unanhängig voneinander vorliegen (die Neigung hängt nicht von der Reibung ab und umgekehrt), können alle Bestandteile, also beide Beschleunigungen und die konstante Geschwindigkeit nacheinander eingesetzt werden. Das führt dann zu
\begin{align} s(1,2 \text{ s}) &= \frac12 \left(0,5 - 0,3 \right) \; \frac{\text{m}}{\text{s}^2} \cdot \left(1,2 \text{ s} \right)^2 + 1,5 \; \frac{\text{m}}{\text{s}} \cdot 1,2 \text{ s} \\ \\ s &= 1,944 \text{ m} \end{align}Für die nächste Aufgabe wird der gleiche Ansatz verfolgt:
$$ s(t) = \frac12 \cdot a_1 \cdot t^2 + \frac12 \cdot a_2 \cdot t^2 + v_0 \cdot t $$Da der zurückgelegte Weg bekannt ist, muss die Gleichung nach $t$ umgestellt werden. Da $t$ aber sowohl linear als auch quadratisch vorkommt, wird hier die $pq-$Formel zur Lösung einer quadratischen Gleichung benötigt. Durch Umstellen erhält man:
\begin{align} 3 \text{ m} &= \frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 1,5 \; \frac{\text{m}}{\text{s}} \cdot t \\ \\ 0 &= \frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} \cdot t^2 + 1,5 \; \frac{\text{m}}{\text{s}} \cdot t - 3 \text{ m} \\ \\ 0 &= t^2 + \frac{1,5 \; \frac{\text{m}}{\text{s}}}{\frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2}} \cdot t - \frac{3 \text{ m}}{\frac12 \cdot 0,2 \; \frac{\text{m}}{\text{s}^2}} \\ \\ 0 &= t^2 + 15 \text{ s} \cdot t - 30 \text{ s}^2 \\ \\ t_{1,2} &= - 7,5 \text{ s} \pm \sqrt{\left(7,5 \text{ s}\right)^2 + 30 \text{ s}^2} \\ \\ t_{1,2} &= - 7,5 \text{ s} \pm \sqrt{86,25 \text{ s}^2} \\ \\ t_1 = - 16,79 \text{ s} \qquad &\vee \qquad t_2 = 1,79 \text{ s} \end{align}Das Ergebnis für $t_1$ ist physikalisch nicht sinnvoll, da es in der Vergangenheit liegt. Die Lösung ist demnach $t = 1,79 \text{ s}$.
Die dritte Aufgabe wird nach den folgenden Ansätzen gelöst:
\begin{align} s &= \frac12 a_1 t^2 + \frac12 a_2 t^2 + v_0 t \\ v &= a_1 t + a_2 t + v_0 \end{align}Hintergrund ist wieder, dass sich die Bewegungszustände ungestört überlagern. Beide Gleichungen werden etwas kompakter notiert:
\begin{align} s &= \frac12 (a_1 + a_2) t^2 + v_0 t \\ \\ v &= (a_1 + a_2) t + v_0\\ t &= \frac{v - v_0}{(a_1 + a_2)} \end{align}Einsetzen führt zu
\begin{align} s &= \frac12 (a_1 + a_2) \left(\frac{v - v_0}{(a_1 + a_2)}\right)^2 + v_0 \frac{v - v_0}{(a_1 + a_2)} \\ \\ s &= \frac{(v - v_0)^2}{2(a_1 + a_2)} + \frac{v_0 (v - v_0)}{(a_1 + a_2)} \end{align}An dieser Stelle müssen erstmal die beiden Brüche bearbeitet werden:
\begin{align} s &= \frac{(v - v_0)^2}{2(a_1 + a_2)} + \frac{v_0 (v - v_0)}{(a_1 + a_2)} \\ \\ s &= \frac{(v - v_0)^2}{2(a_1 + a_2)} + \frac{2v_0 (v - v_0)}{2(a_1 + a_2)} \\ \\ s &= \frac{(v^2 - 2vv_0 + v_0^2)}{2(a_1 + a_2)} + \frac{(2vv_0 - 2v_0^2)}{2(a_1 + a_2)} \\ \\ s &= \frac{v^2 - 2vv_0 + v_0^2 + 2vv_0 - 2v_0^2}{2(a_1 + a_2)} \\ \\ s &= \frac{v^2 - v_0^2}{2(a_1 + a_2)} \end{align}Auflösen nach $v$:
\begin{align} 2s(a_1 + a_2) &= v^2 - v_0^2 \\ \\ 2s(a_1 + a_2) + v_0^2 &= v^2 \\ \\ v &= \sqrt{2s(a_1 + a_2) + v_0^2} \\ \\ v &= \sqrt{2 \cdot 1,5 \text{ m} \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} + \left(1,5 \; \frac{\text{m}}{\text{s}}\right)^2} \\ \\ v &= 1,69 \; \frac{\text{m}}{\text{s}} \end{align}Das ist die Geschwindigkeit bei $s = 1,5 \text{m}$. Mit der gleichen Formel wird auch die Geschwindigkeit bei $s = 3 \text{ m}$ bestimmt:
\begin{align} v &= \sqrt{2 \cdot 3 \text{ m} \cdot 0,2 \; \frac{\text{m}}{\text{s}^2} + \left(1,5 \; \frac{\text{m}}{\text{s}}\right)^2} \\ \\ v &= 1,86 \; \frac{\text{m}}{\text{s}} \end{align}| gleichförmige Bewegung | ||
| Randbedingungen | $s_0 = 0$ $v_0 = \text{ konstant}$ $v_0 > 0$ | $s_0 \neq 0$ $v_0 = \text{ konstant}$ $v_0 > 0$ |
| Zeit-Weg-Gesetz | $s(t)=v \cdot t$ | $s(t)=v \cdot t + s_0$ |
| t-s-Diagramm | 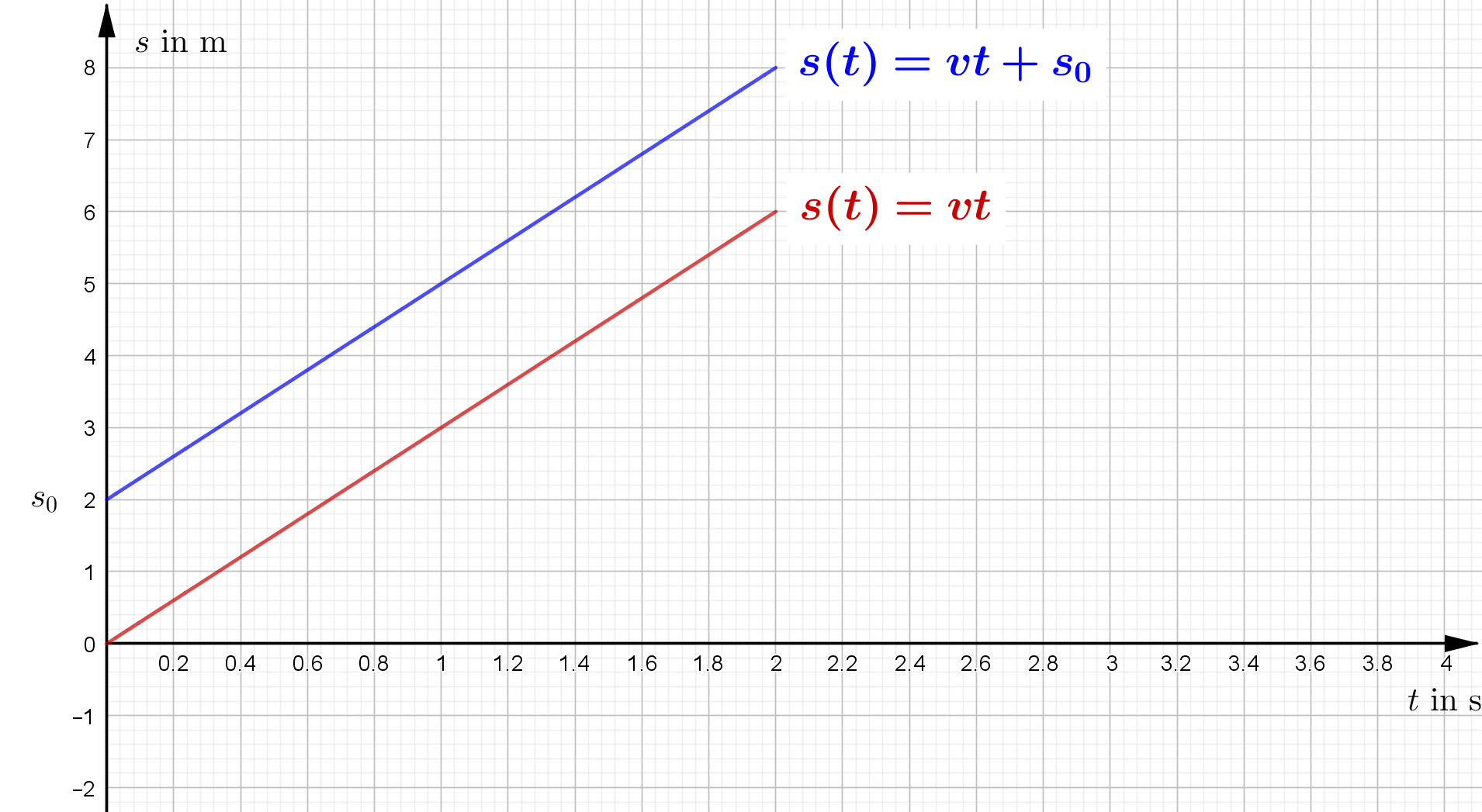 |
|
| Zeit-Geschwindigkeit-Gesetz | $v(t)=v_0$ | |
| t-v-Diagramm | 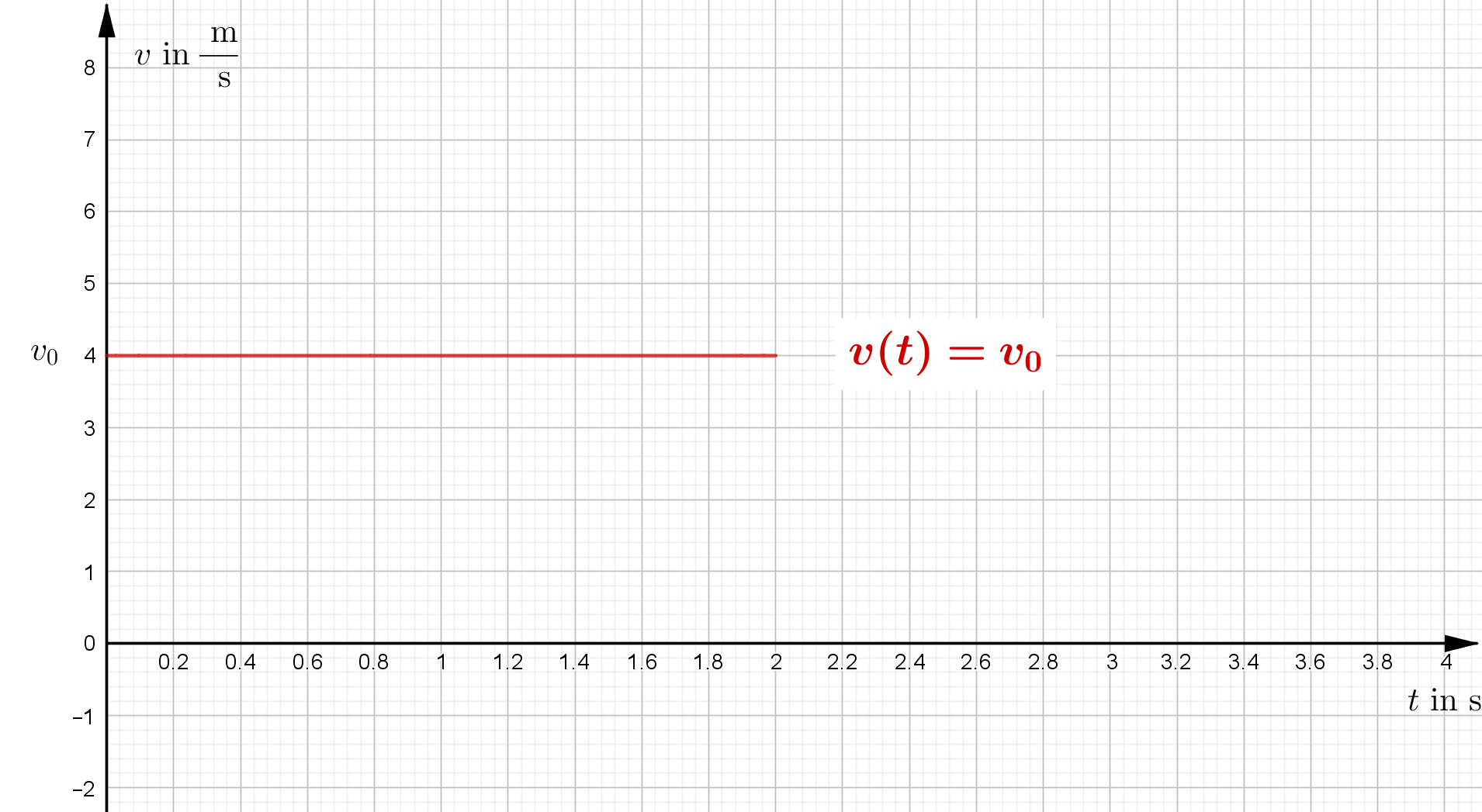 |
|
| Zeit-Beschleunigung-Gesetz | $a(t)=0$ | |
| t-a-Diagramm | 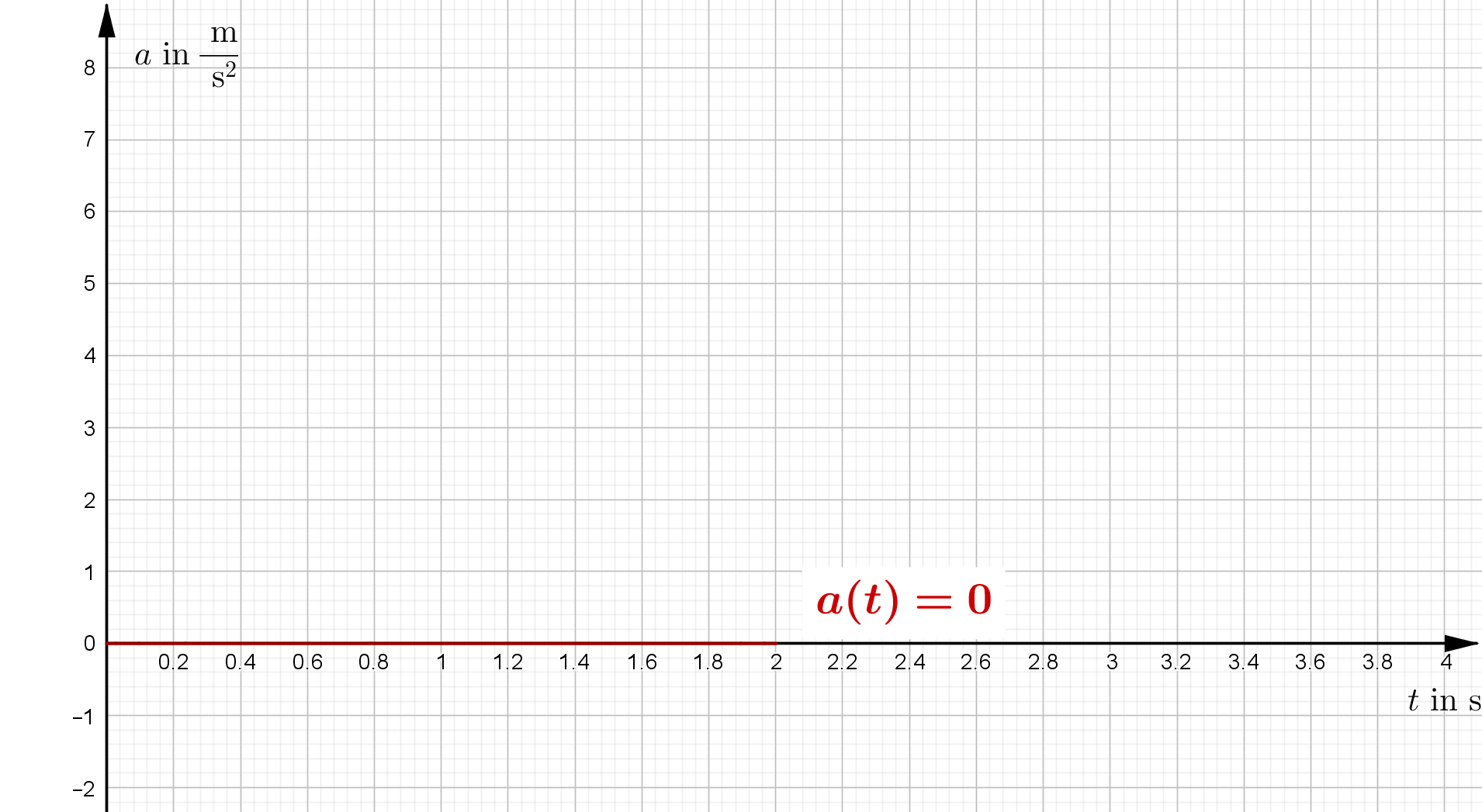 |
|
| konstant beschleunigte Bewegung | |||
| Randbedingungen | $s_0 = 0$ $v_0 = 0$ $a > 0$ | $s_0 \neq 0$ $v_0 = 0$ $a > 0$ | $s_0 \neq 0$ $v_0 \neq 0$ $a > 0$ |
| Zeit-Weg-Gesetz | $s(t)=\frac12 \cdot a \cdot t^2$ | $s(t)=\frac12 \cdot a \cdot t^2 + s_0$ | $s(t)=\frac12 \cdot a \cdot t^2 + v_0 \cdot t + s_0$ |
| t-s-Diagramm | 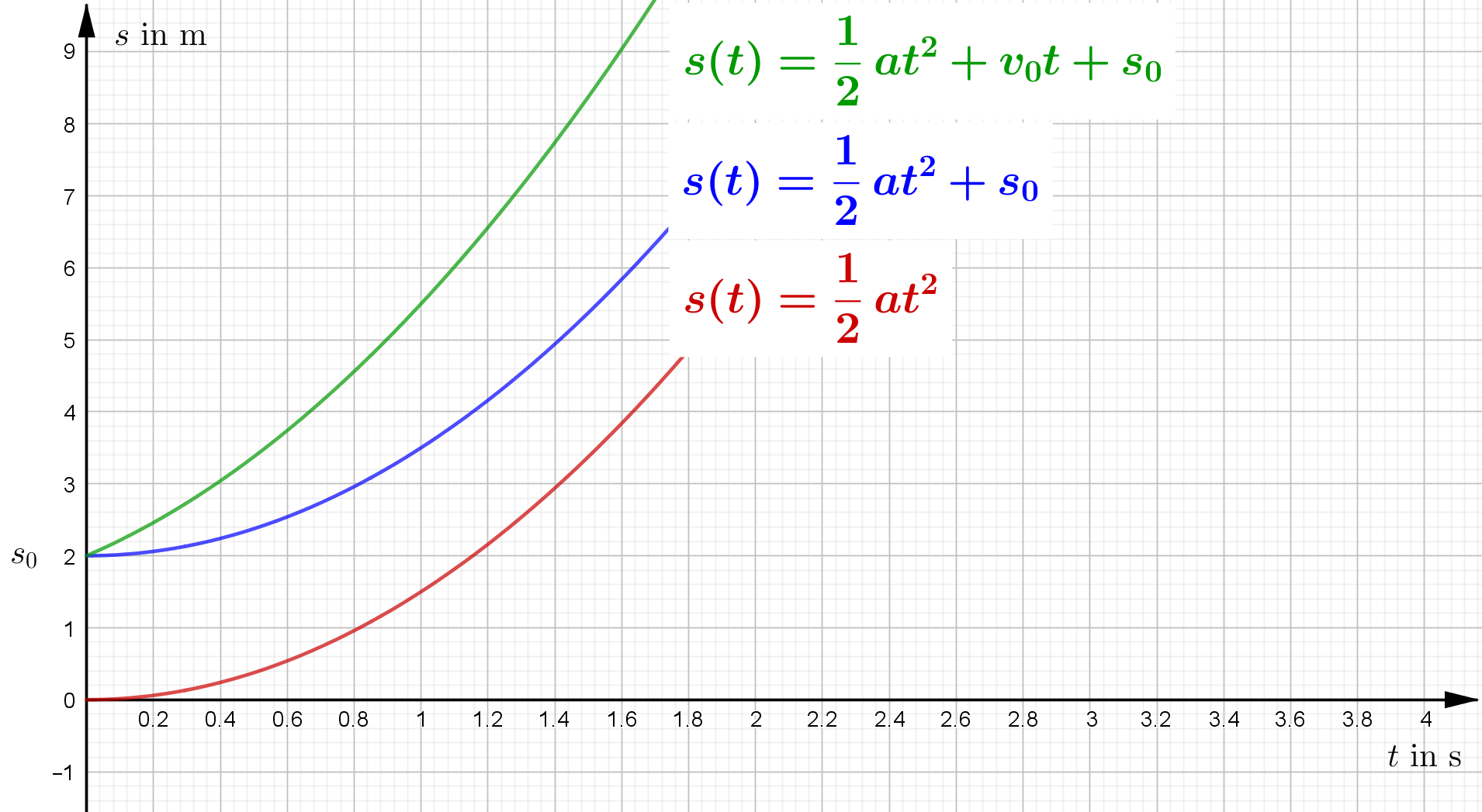 |
||
| Zeit-Geschwindigkeit-Gesetz | $v(t)=a \cdot t$ | $v(t)=a \cdot t + v_0$ | |
| t-v-Diagramm |  |
||
| Zeit-Beschleunigung-Gesetz | $a(t)=a$ | ||
| t-a-Diagramm | 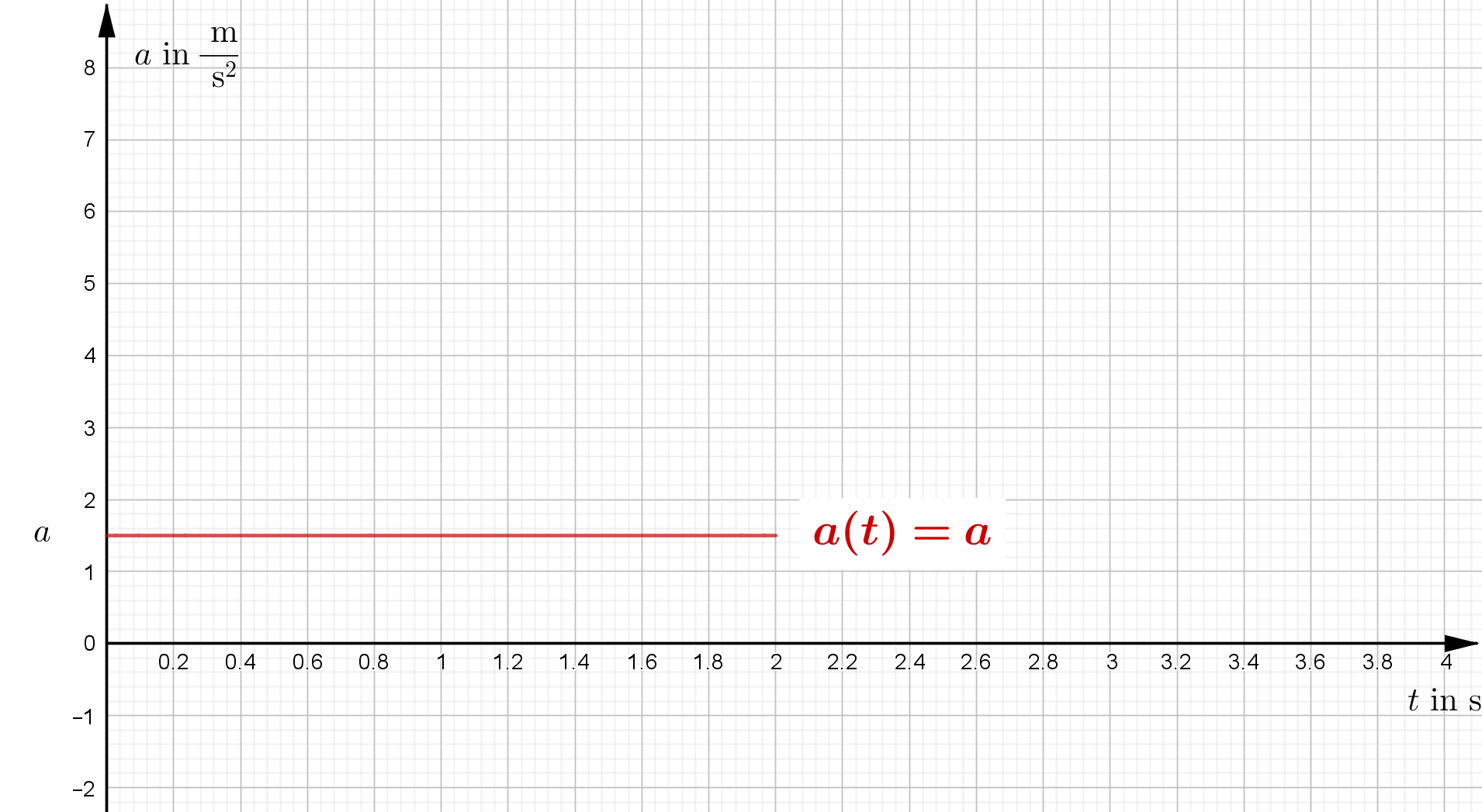 |
||
Analog zu der Bewegung entlang einer Linie wird zunächst die Bewegung auf einer Kreisbahn beschrieben. Dafür sind einige neue und zusätzliche Begriffe und Größen notwendig. Die Ursache einer Kreisbewegung soll im Anschluss erläutert werden (Zentripetalkraft).
Neben dem Begriff Zeit t werden die weiteren Größen aus der geradlinigen Bewegung etwas verändert dargestellt. Die Strecke s
bleibt häufig einfach die Strecke s, in manchen Fällen wird die bei einer Kreisbewegung zurückgelegte Strecke auch Bogen oder
Kreisbogen b genannt. Die Geschwindigkeit v wird meist als Bahngeschwindigkeit bezeichnet, ebenso die
Beschleunigung a als Bahnbeschleunigung.
Neue Größen oder Bezeichnungen sind der Radius r der Kreisbahn, die Dauer einer Bewegung auf einem Vollkreis, Umlaufzeit T,
die Anzahl von Umläufen pro Sekunde, Frequenz f, sowie die Strecke für einen Umlauf, den Umfang U.
Zunächst soll noch eine kleine Einschränkung gemacht werden: Die Bewegung auf der Kreisbahn erfolgt mit konstanter Bahngeschwindigkeit. Die Bewegung
wird dann als gleichförmige Kreisbewegung bezeichnet. Die Begriffe noch einmal aufgelistet und mit ihren Einheiten versehen:
$$
\text{Kreisbogen} \; b \\
[b] = 1 \; \text{m} \\
\\
\text{Bahngeschwindigkeit} \; v \\
[v] = 1 \; \frac{\text{m}}{\text{s}} \\
\\
\text{Bahnbeschleunigung} \; a \\
[a] = 1 \; \frac{\text{m}}{\text{s}^2} \\
\\
\text{Radius} \; r \\
[r] = 1 \; \text{m} \\
\\
\text{Umlaufzeit} \; T \\
[T] = 1 \; \text{s} \\
\\
\text{Frequenz} \; f \\
[f] = 1 \; \text{Hz} \\
\\
\text{Winkelgeschwindigkeit} \; \omega \\
[\omega] = 1 \; \text{s}^{-1}
$$
Die Einheit der Frequenz lautet eigentlich $s^{-1}$, d.h. Anzahl von Umläufen pro Sekunde, wurde aber zu Ehren des Physikers
Heinrich Hertz nach diesem benannt: $1 Hz = 1 s^{-1}$.
Es gelten die folgenden Beziehungen:
\begin{align}
T = \frac{1}{f} \qquad &; \qquad f = \frac{1}{T} \\ \\
U &= 2 \pi r \\ \\
v = \frac{b}{t} = \frac{U}{T} &= \frac{2 \pi r}{T} = 2 \pi r f
\end{align}
Die neue Größe Winkelgeschwindigkeit bedarf einer näheren Beschreibung.
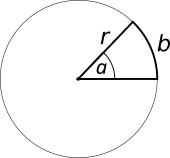 Dem Winkel $\alpha$ wird das Verhältnis von Kreisbogen und Radius zugeordnet.
$$
\alpha \; \rightarrow \; \frac{b}{r}
$$
Mit der Winkelgeschwindigkeit wird ausgedrückt, welcher Winkel $\alpha$ in einer Zeit $t$ überstrichen wird, also $\omega = \frac{\alpha}{t}$. Mit
der Zuordnung $\alpha \rightarrow \frac{b}{r}$ wird das zu: $\omega = \frac{b}{r \cdot t}$. Da es sich um eine gleichförmige Geschwindigkeit
handelt, also in jeder Zeiteinheit der selbe Winkel überstrichen wird, folgt mit $b = 2 \pi r$, wenn $t = T$:
$$
\omega = \frac{2 \pi}{T}
$$
oder alternativ
$$
\omega = 2 \pi f
$$
Aus der letzten Gleichung folgt, dass die Frequenz und die Winkelgeschwindigkeit (auch als Kreisfrequenz bezeichnet) die gleiche Einheit
haben. Im Unterschied zur Frequenz bleibt es bei $\omega$ bei der Einheit $s^{-1}$.
Dem Winkel $\alpha$ wird das Verhältnis von Kreisbogen und Radius zugeordnet.
$$
\alpha \; \rightarrow \; \frac{b}{r}
$$
Mit der Winkelgeschwindigkeit wird ausgedrückt, welcher Winkel $\alpha$ in einer Zeit $t$ überstrichen wird, also $\omega = \frac{\alpha}{t}$. Mit
der Zuordnung $\alpha \rightarrow \frac{b}{r}$ wird das zu: $\omega = \frac{b}{r \cdot t}$. Da es sich um eine gleichförmige Geschwindigkeit
handelt, also in jeder Zeiteinheit der selbe Winkel überstrichen wird, folgt mit $b = 2 \pi r$, wenn $t = T$:
$$
\omega = \frac{2 \pi}{T}
$$
oder alternativ
$$
\omega = 2 \pi f
$$
Aus der letzten Gleichung folgt, dass die Frequenz und die Winkelgeschwindigkeit (auch als Kreisfrequenz bezeichnet) die gleiche Einheit
haben. Im Unterschied zur Frequenz bleibt es bei $\omega$ bei der Einheit $s^{-1}$.
Für die Beziehung zwischen Bahngeschwindigkeit und Winkelgeschwindigkeit folgt: \begin{align} v = 2 \pi r f \qquad &; \qquad \omega = 2 \pi f \\ v &= \omega \cdot r \end{align} Das Verhältnis Kreisbogen zu Radius ist ein anderer Ausdruck für den Winkel. Der Winkel wird in Grad (°) angegeben, $\frac{b}{r}$ ist eine einheitenlose Zahl und wird als Bogenmaß bezeichnet. Als Einheit dient der Radiant (rad). Aus dem Zusammenhang für den Vollkreis gilt: \begin{align} 360° &\hat{=} \; 2 \pi \; \text{ rad} \\ 180° &\hat{=} \; \pi \; \text{rad} \\ 90° &\hat{=} \; \frac{\pi}{2} \; \text{rad} \\ 30° &\hat{=} \; \frac{\pi}{6} \; \text{rad} \end{align}
© mondbrand MMXIX