

Jeder Punkt, der in einem dreidimensionalen Koordinatensystem positioniert werden soll, benötigt drei Koordinaten, die hier mit $x_1$, $x_2$ und $x_3$
bezeichnet werden.
Die drei Koordinaten sind Angaben, um wieviele Längeneinheiten man sich in die entsprechende Richtung bewegen muss.
Das Koordiantensystem selbst ist so orientiert, dass die $x_1$-Achse in die Richtung des ausgestreckten Daumens der rechten Hand zeigt, die
$x_2$-Achse in die Richtung des Zeigefingers und die $x_3$-Achse in die des Mittelfingers, wobei zwischen den Fingern immer ein
rechter Winkel ist (rechtsdrehendes Koordinatensystem).
 In der Abbildung ist die $x_1$-Achse in rot, die $x_2$-Achse in grün und die $x_3$-Achse in blau dargestellt.
In der Abbildung ist die $x_1$-Achse in rot, die $x_2$-Achse in grün und die $x_3$-Achse in blau dargestellt.
Die Punkte im Koordinatensystem haben jeweils einen Ortsvektor, der vom Koordinatenursprung zum Punkt zeigt. In der Abbildung ist das der Punkt $A$, auf den vom Ursprung aus mit dem Ortsvektor $\vec a$ gezeigt wird. Es gilt: \begin{align} A (x_1 / x_2 / x_3) \qquad &\Longleftrightarrow \qquad \vec a = \left( \begin{array}{} x_1 \\ x_2 \\ x_3 \end{array} \right) \\ \text{Punkt} \qquad &\Longleftrightarrow \qquad \text{Ortsvektor} \end{align}
Jeder Ortsvektor ist die Summe der Vektoren, die in die Koordinatenachsenrichtungen zeigen. In der Abbildung für den Ortsvektor $\vec a$ ist das $$ \vec a = \left( \begin{array}{} x_1 \\ 0 \\ 0 \end{array} \right) + \left( \begin{array}{} 0 \\ x_2 \\ 0 \end{array} \right) + \left( \begin{array}{} 0 \\ 0 \\ x_3 \end{array} \right) $$ Aus der Abbildung wird außerdem ersichtlich, dass der Ortsvektor die Raumdiagonale des Quaders ist, dessen Kanten von den Vektoren in Achsenrichtung gebildet werden. Die Reihenfolge der Addition ist offensichtlich nicht wichtig.
Es wäre sinnvoll, die Vektoren in Achsenrichtung so zu gestalten, dass sie genau eine Längeneinheit weit zeigen. Es ist klar, dass sie dann die
Länge Eins haben. In diesem Fall nennt man diese Vektoren auch Einheitsvektoren in die jeweilige Achsenrichtung, z.B. $\vec x_{1,0}$.
Multipliziert man die Einheitsvektoren mit einem Faktor $k$, entstehen die Vektoren, wie sie in der Abbildung zu sehen sind. Der Faktor
$k$ entspricht dann der Länge der Seite des Quaders, wohingegen der Einheitsvektor lediglich die Richtung, d.h. die Orientierung des
Quaderkante angibt.
\begin{align}
\vec x_1 &= k \cdot \vec x_{1,0} \\
\vec x_1 &= 2 \cdot \left( \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right) \\
\vec x_1 &= \left( \begin{array}{} 2 \\ 0 \\ 0 \end{array} \right)
\end{align}
Jeder Ortsvektor ist die Summe von Vielfachen der Einheitsvektoren in den drei Achsenrichtungen $x_1$, $x_2$ und $x_3$.
Der Einheitsvektor eines beliebigen Vektors bekommt man, wenn man den Vektor durch seinen Betrag teilt. Es gilt: \begin{align} \vec a_0 &= \frac{\vec a}{\lvert \vec a \rvert} \end{align}
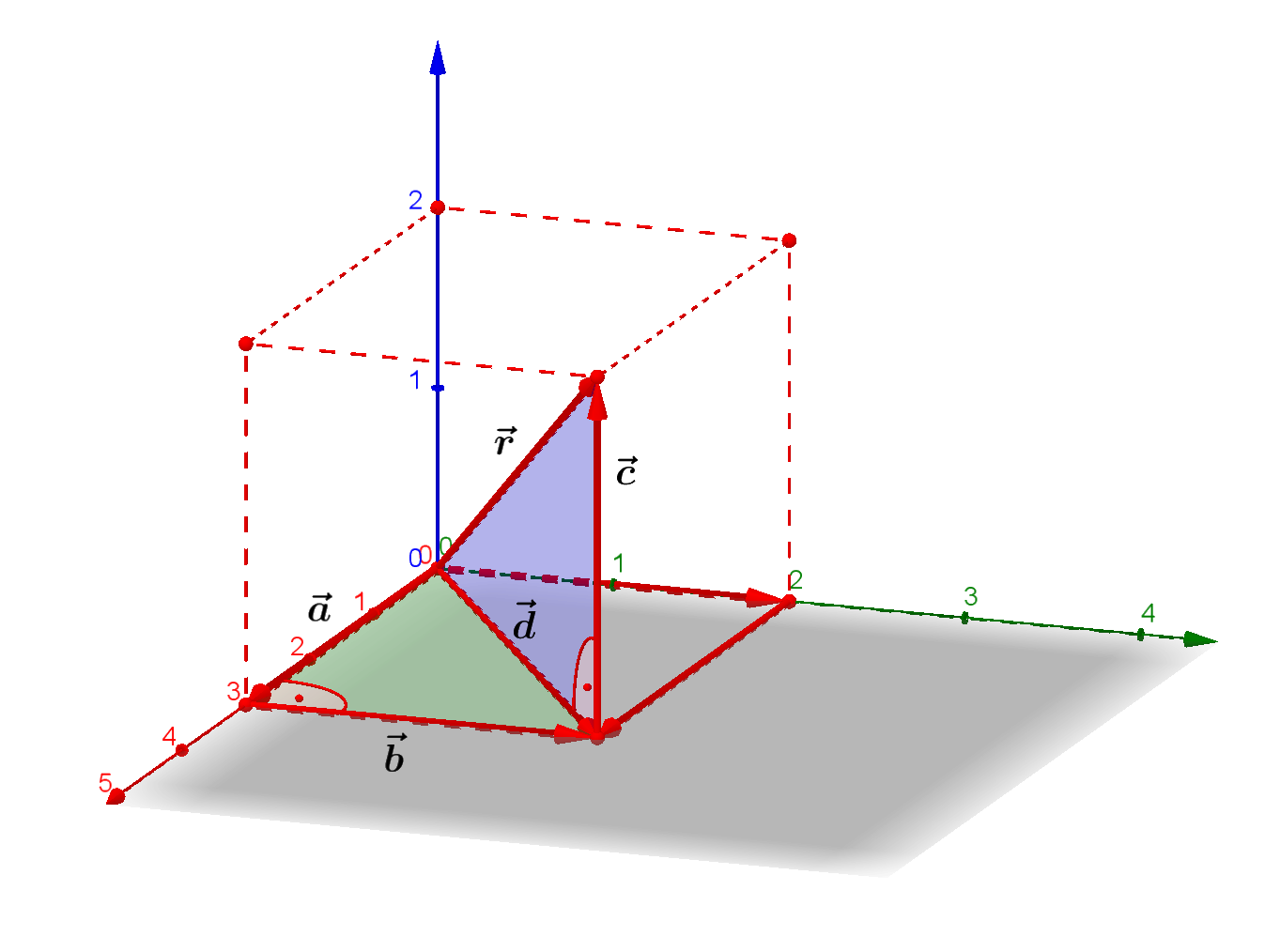 Der Betrag eines Vektors ist seine Länge. Um die Länge zu bestimmen, wird der Satz des Pythagoras zweimal benötigt. Aus der Abbildung wird das
deutlich. Es ergibt sich zunächst für den Betrag des Vektors $\vec d$ die folgende Rechnung:
\begin{align}
\lvert \vec d \rvert &= \sqrt{\lvert \vec a \rvert ^2 + \lvert \vec b \rvert ^2} \\
\end{align}
Für den Betrag des Vektors $\vec r$ ergibt sich dann:
\begin{align}
\lvert \vec r \rvert &= \sqrt{\lvert \vec d \rvert ^2 + \lvert \vec c \rvert ^2} \\
\lvert \vec r \rvert &= \sqrt{\lvert \vec a \rvert ^2 + \lvert \vec b \rvert ^2 + \lvert \vec c \rvert ^2}
\end{align}
Mit $\lvert \vec a \rvert = r_1$, $\lvert \vec b \rvert = r_2$ und $\lvert \vec c \rvert = r_3$ ergibt sich für den Betrag des Vektors $\vec r$:
$$
\lvert \vec r \rvert = \sqrt{r_1^2 + r_2^2 + r_3^2}
$$
Im gezeigten Beispiel wäre das:
\begin{align}
\lvert \vec r \rvert &= \sqrt{r_1^2 + r_2^2 + r_3^2} \\
\lvert \vec r \rvert &= \sqrt{3^2 + 2^2 + 2^2} \\
\lvert \vec r \rvert &= \sqrt{17} \\
\lvert \vec r \rvert &= 4,12 \text{ LE}
\end{align}
Der Betrag eines Vektors ist seine Länge. Um die Länge zu bestimmen, wird der Satz des Pythagoras zweimal benötigt. Aus der Abbildung wird das
deutlich. Es ergibt sich zunächst für den Betrag des Vektors $\vec d$ die folgende Rechnung:
\begin{align}
\lvert \vec d \rvert &= \sqrt{\lvert \vec a \rvert ^2 + \lvert \vec b \rvert ^2} \\
\end{align}
Für den Betrag des Vektors $\vec r$ ergibt sich dann:
\begin{align}
\lvert \vec r \rvert &= \sqrt{\lvert \vec d \rvert ^2 + \lvert \vec c \rvert ^2} \\
\lvert \vec r \rvert &= \sqrt{\lvert \vec a \rvert ^2 + \lvert \vec b \rvert ^2 + \lvert \vec c \rvert ^2}
\end{align}
Mit $\lvert \vec a \rvert = r_1$, $\lvert \vec b \rvert = r_2$ und $\lvert \vec c \rvert = r_3$ ergibt sich für den Betrag des Vektors $\vec r$:
$$
\lvert \vec r \rvert = \sqrt{r_1^2 + r_2^2 + r_3^2}
$$
Im gezeigten Beispiel wäre das:
\begin{align}
\lvert \vec r \rvert &= \sqrt{r_1^2 + r_2^2 + r_3^2} \\
\lvert \vec r \rvert &= \sqrt{3^2 + 2^2 + 2^2} \\
\lvert \vec r \rvert &= \sqrt{17} \\
\lvert \vec r \rvert &= 4,12 \text{ LE}
\end{align}
Zwei Vektoren werden addiert, indem die einzelnen Komponenten addiert werden. \begin{align} \vec a + \vec b &= \vec c \\ \left( \begin{array}{} a_1 \\ a_2 \\ a_3 \end{array} \right) + \left( \begin{array}{} b_1 \\ b_2 \\ b_3 \end{array} \right) &= \left( \begin{array}{} c_1 \\ c_2 \\ c_3 \end{array} \right) \\ \left( \begin{array}{} a_1 + b_1 \\ a_2 + b_2 \\ a_3 + b_3 \end{array} \right) &= \left( \begin{array}{} c_1 \\ c_2 \\ c_3 \end{array} \right) \end{align}
Durch die Multiplikation mit einem Faktor $k$ werden Vektoren verlängert $\left( k > 1 \right)$, verkürzt $\left( 0 < k < 1 \right)$ oder umgekehrt $\left( k < 0 \right)$. Jede einzelne Komponente wird dabei mit dem Faktor multipliziert. \begin{align} \vec b &= k \cdot \vec a \\ \left( \begin{array}{} b_1 \\ b_2 \\ b_3 \end{array} \right) &= k \cdot \left( \begin{array}{} a_1 \\ a_2 \\ a_3 \end{array} \right) \\ \left( \begin{array}{} b_1 \\ b_2 \\ b_3 \end{array} \right) &= \left( \begin{array}{} k \cdot a_1 \\ k \cdot a_2 \\ k \cdot a_3 \end{array} \right) \end{align}
Zwei Vektoren sind genau dann linear abhängig, wenn man einen der Vektoren durch ein vielfaches des anderen Vektors ersetzen kann. Für lineare Abhängigkeit
muss also gelten:
$$
\vec a = k \cdot \vec b
$$
Diese (Vektor-)Gleichung besteht aus drei einzelnen Gleichungen, in denen jeweils ein $k-Wert$ vorkommt. Ist $k$ in allen drei Gleichungen identisch,
sind die Vektoren $\vec a$ und $\vec b$ linear abhängig. Ist der Wert für $k$ nicht konstant, sind sie es nicht. In anderen Worten: Sie zeigen
entlang unterschiedlicher Richtungen.
Mehrere Vektoren sind dann linear abhängig, wenn sie oder vielfache von sich addiert den Nullvektor ergeben:
$$
k_1 \cdot \vec a + k_2 \cdot \vec b + k_3 \cdot \vec c + \cdots = \vec 0
$$
Wenn man also einen geschlossenen Kreislauf mit den Vektoren erhält, dann sind sie linear abhängig.
Geometrisch ist das Skalarprodukt zweier Vektoren die Projektion des einen Vektors auf den anderen Vektor.
Das Skalarprodukt allgemein lautet folgendermaßen:
\begin{align}
\vec a \cdot \vec b &= \left( \begin{array}{} a_1 \\ a_2 \\ a_3 \end{array} \right) \cdot \left( \begin{array}{} b_1 \\ b_2 \\ b_3 \end{array} \right) \\
\vec a \cdot \vec b &= \left( a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3 \right)
\end{align}
Das Ergebnis der Skalarmultiplikation ist ein Skalar, also eine Zahl und damit kein Vektor.
Mehr über das Skalarprodukt hier
Für den Winkel zwischen den Vektoren gilt:
\begin{align}
\cos \alpha &= \frac{\vec a \cdot \vec b}{\lvert \vec a \rvert \cdot \lvert \vec b \rvert}
\end{align}
Beispiel:
Gegeben sind die beiden Vektoren
$$
\vec a = \left( \begin{array}{} 3 \\ 3 \\ 1 \end{array} \right) \qquad \text{und} \qquad \vec b = \left( \begin{array}{} 6 \\ 0 \\ 3 \end{array} \right)
$$
Welcher Winkel wird zwischen den Vektoren aufgespannt?
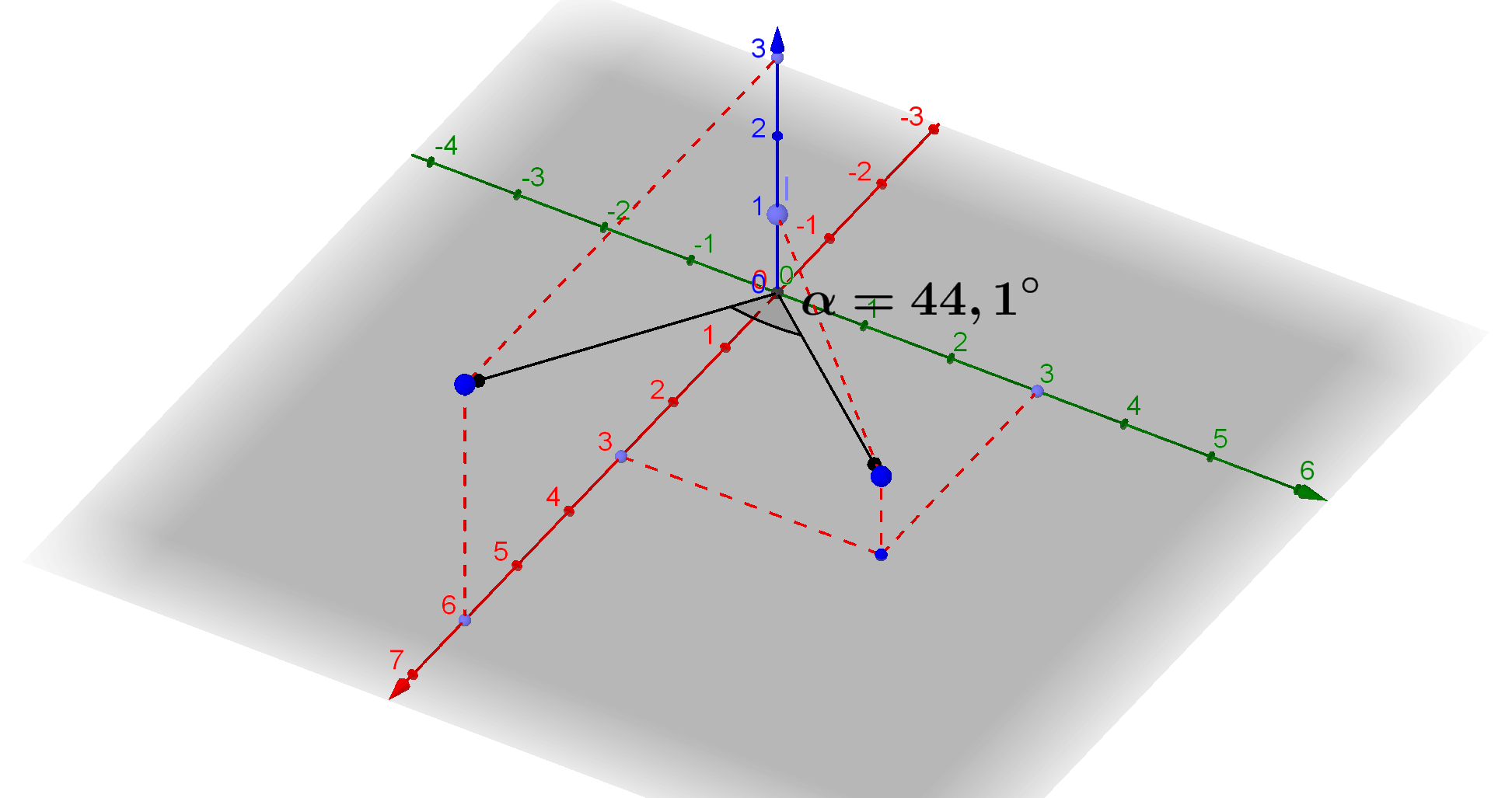 \begin{align}
\cos \alpha &= \frac{\left( \begin{array}{} 3 \\ 3 \\ 1 \end{array} \right) \cdot \left( \begin{array}{} 6 \\ 0 \\ 3 \end{array} \right)}{\sqrt{3^2 +3^2 +1^2} \cdot \sqrt{6^2 + 0^2 + 3^2}} \\\\
\cos \alpha &= \frac{3 \cdot 6 + 3 \cdot 0 + 1 \cdot 3}{\sqrt{19} \cdot \sqrt{45}} \\\\
\cos \alpha &= \frac{21}{29,24} \\\\
\cos \alpha &= 0,718 \\\\
\alpha &= \cos^{-1} \left(0,718 \right) \\\\
\alpha &= 44,1\text{°}
\end{align}
\begin{align}
\cos \alpha &= \frac{\left( \begin{array}{} 3 \\ 3 \\ 1 \end{array} \right) \cdot \left( \begin{array}{} 6 \\ 0 \\ 3 \end{array} \right)}{\sqrt{3^2 +3^2 +1^2} \cdot \sqrt{6^2 + 0^2 + 3^2}} \\\\
\cos \alpha &= \frac{3 \cdot 6 + 3 \cdot 0 + 1 \cdot 3}{\sqrt{19} \cdot \sqrt{45}} \\\\
\cos \alpha &= \frac{21}{29,24} \\\\
\cos \alpha &= 0,718 \\\\
\alpha &= \cos^{-1} \left(0,718 \right) \\\\
\alpha &= 44,1\text{°}
\end{align}
Das kartesische dreidimensionale Koordinatensystem ist ein Ergebnis des Vektorprodukts. Werden zwei Vektoren vektoriell multipliziert,
entsteht ein dritter Vektor, der auf den beiden anderen jeweils senkrecht steht. Es heißt:
$$
\vec a \times \vec b = \vec c
$$
Die Reihenfolge lässt sich wie bei den Koordinatenachsen an der rechten Hand ablesen: Vektor $\vec a$ ist der Daumen, $\vec b$ der Zeigefinger
und $\vec c$ der Mittelfinger.
Die Berechnungsvorschrift:
$$
\vec a \times \vec b = \left( \begin{array}{} a_2 \cdot b_3 - a_3 \cdot b_2 \\ a_3 \cdot b_1 - a_1 \cdot b_3 \\ a_1 \cdot b_2 - a_2 \cdot b_1 \end{array} \right)
$$
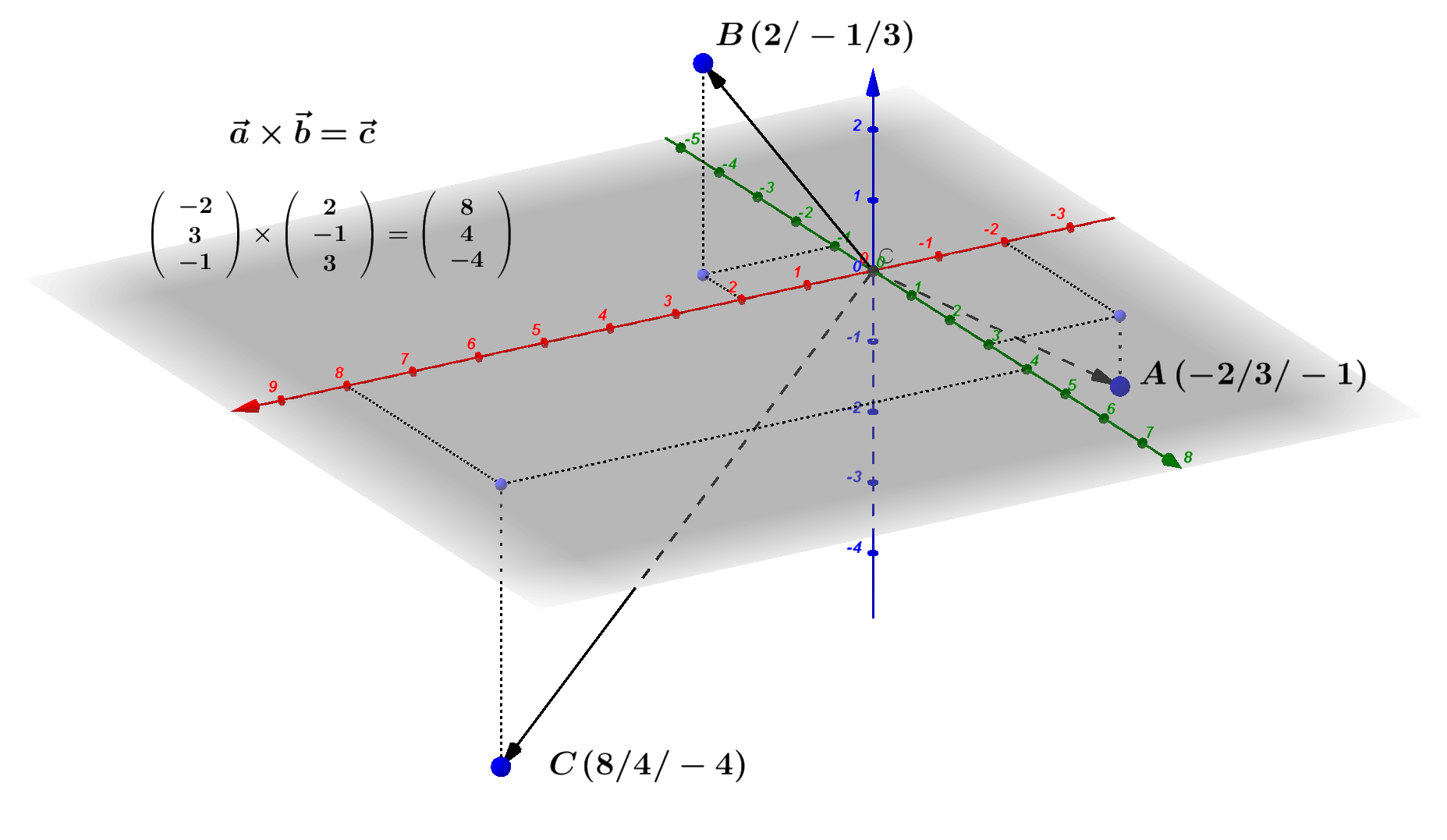
Das gezeigte Beispiel mit Zahlen:
\begin{align}
\vec a \times \vec b &= \left( \begin{array}{center} -2 \\ 3 \\ -1 \end{array} \right) \times \left( \begin{array}{center} 2 \\ -1 \\ 3 \end{array} \right) \\
\vec a \times \vec b &= \left( \begin{array}{center} 3 \cdot 3 - (-1) \cdot (-1) \\ (-1) \cdot 2 - (-2) \cdot 3 \\ (-2) \cdot (-1) - 3 \cdot 2 \end{array} \right) \\
\vec a \times \vec b &= \left( \begin{array}{center} 8 \\ 4 \\ -4 \end{array} \right) \\
\vec c &= \left( \begin{array}{center} 8 \\ 4 \\ -4 \end{array} \right)
\end{align}
Mehr über das Vektorprodukt hier
© mondbrand MMXIX