

Gegeben ist ein Quader mit den Eckpunkten
$$
A \left( 3 \mid 2 \mid -1 \right) \\
B \left( 3 \mid 4 \mid -2 \right) \\
C \left( 3 \mid 4 \mid 3 \right) \\
D \left( 3 \mid 6 \mid 2 \right) \\
E \left( -1 \mid 2 \mid -1 \right) \\
F \left( -1 \mid 4 \mid -2 \right) \\
G \left( -1 \mid 4 \mid 3 \right) \\
H \left( -1 \mid 6 \mid 2 \right)
$$
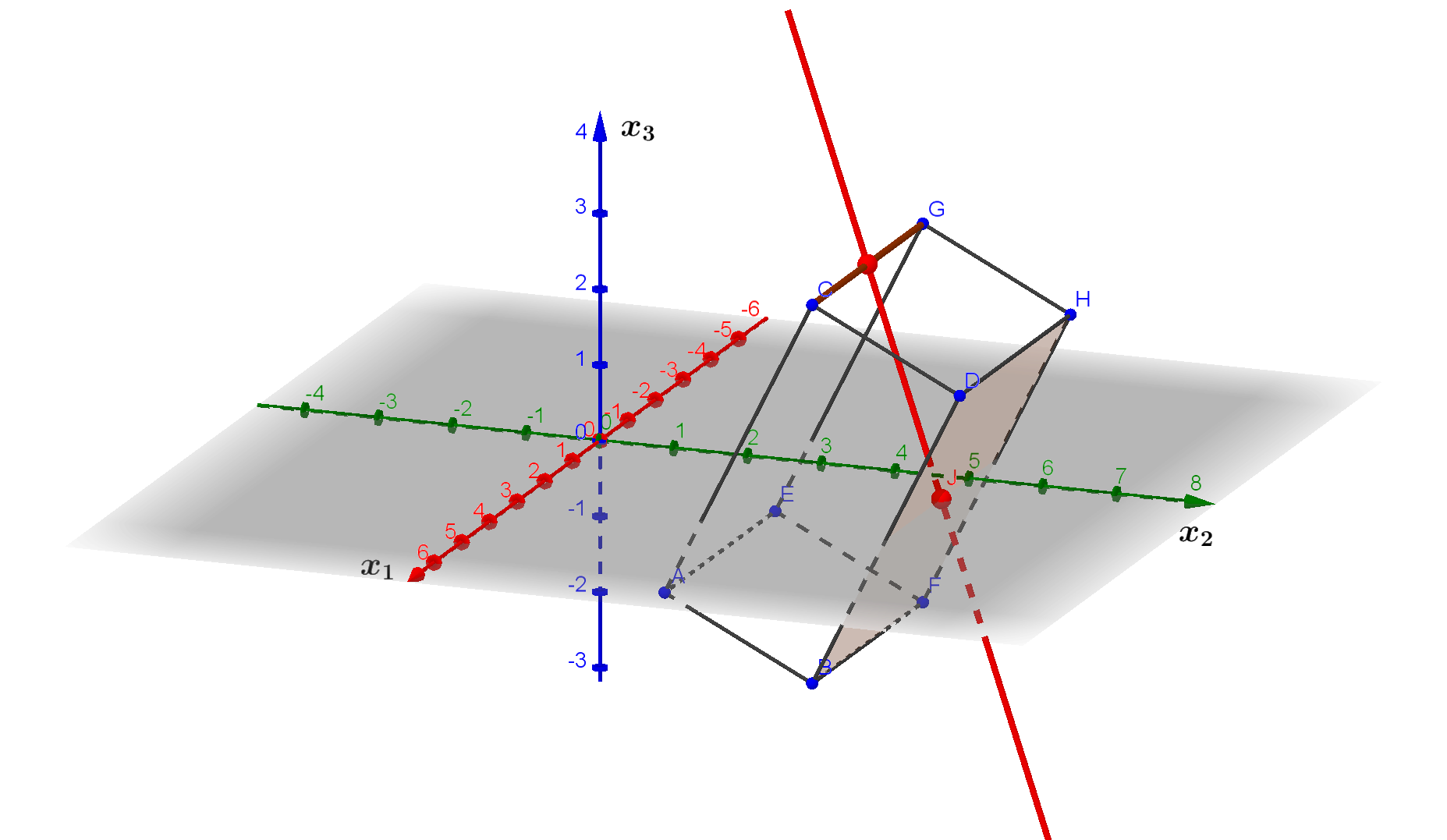
Für den Mittelpunkt der Strecke $\overline{CG}$ werden jeweils der Mittelpunkt der $x_1$-, $x_2$- und $x_3$-Werte benötigt. Das führt zu dem Ansatz: $$ \vec m_{CG} = \frac{\vec c + \vec g}{2} = \frac12 \cdot \left( \vec c + \vec g \right) $$ Der gleiche Ansatz entsteht, wenn man vom Ursprung zum Punkt $C$ geht (Ortsvektor $\vec c$) und dann die Hälfte des Vektors $\overrightarrow{CG}$ addiert. \begin{align} \vec m_{CG} &= \vec c + \frac12 \cdot \overrightarrow{CG} \\ \\ \vec m_{CG} &= \vec c + \frac12 \cdot \left( \vec g - \vec c \right) \\ \\ \vec m_{CG} &= \vec c + \frac12 \cdot \vec g - \frac 12 \cdot \vec c \\ \\ \vec m_{CG} &= \frac12 \cdot \vec c + \frac12 \cdot \vec g \\ \\ \vec m_{CG} &= \frac12 \cdot \left( \vec c + \vec g \right) \end{align} Der Mittelpunkt der Strecke $\overline{CG}$ hat den Ortsvektor $\vec m_{CG} = \left( \begin{array}{} 1 \\ 4 \\ 3 \end{array} \right)$.
Der Mittelpunkt der Fläche $BDHF$ lässt sich herausfinden, indem man beachtet, dass es sich um ein Quader handelt. EIn Quader hat rechteckige
Seitenflächen. Also ist auch die Fläche $BDHF$ ein Rechteck. Der Flächenmittelpunkt eines Rechtecks ist auch der Mittelpunkt zweier gegenüberliegender
Eckpunkte, z.B. der Punkte $D$ und $F$. Der Mittelpunkt zwischen den beiden Punkten folgt aus $\vec m_{DF} = \frac12 \left( \vec d + \vec f \right)$.
Der Ortsvektor des Flächenmittelpunkts lautet somit: $\vec m_{DF} = \left( \begin{array}{} 1 \\ 5 \\ 0 \end{array} \right)$.
Mit dem Mittelpunkt der Strecke $\overline {CG}$ als Stützvektor und dem Verbindungsvektor zwischen $\vec m_{CG}$ und $\vec m_{DF}$ als Richtungsvektor kann man die Geradengleichung aufstellen: \begin{align} g: \vec x &= \vec m_{CG} + r \cdot \left( \vec m_{DF} - \vec m_{CG} \right) \\ \\ g: \vec x &= \left( \begin{array}{} 1 \\ 4 \\ 3 \end{array} \right) + r \cdot \left( \left( \begin{array}{} 1 \\ 5 \\ 0 \end{array} \right) - \left( \begin{array}{} 1 \\ 4 \\ 3 \end{array} \right) \right) \\ \\ g: \vec x &= \left( \begin{array}{} 1 \\ 4 \\ 3 \end{array} \right) + r \cdot \left( \begin{array}{} 0 \\ 1 \\ -3 \end{array} \right) \end{align}
Die gesuchte Strecke ist der Abstand der beiden ermittelten Mittelpunkte bzw. die Länge des Verbindungsvektors der beiden Punkte: \begin{align} s &= \left\vert \left( \left( \begin{array}{} 1 \\ 5 \\ 0 \end{array} \right) - \left( \begin{array}{} 1 \\ 4 \\ 3 \end{array} \right) \right) \right\vert \\ \\ s &= \left\vert \left( \begin{array}{} 0 \\ 1 \\ -3 \end{array} \right) \right\vert \\ \\ s &= \sqrt{0^2 + 1^2 + (-3)^2} \\ \\ s &= \sqrt{10} \end{align} Die Strecke, die die Gerade durch den Quader verläuft, hat also die Länge von etwa 3,16 LE.
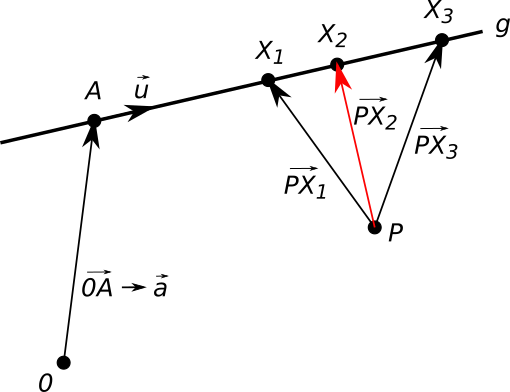 Gegeben ist ein Punkt und eine Gerade:
$$
P (2 \mid 1 \mid -1) \\
g: \vec x = \left( \begin{array}{} 1 \\ 1 \\ 1 \end{array} \right) + r \cdot \left( \begin{array}{} 0 \\ 0 \\ 4 \end{array} \right)
$$
Gegeben ist ein Punkt und eine Gerade:
$$
P (2 \mid 1 \mid -1) \\
g: \vec x = \left( \begin{array}{} 1 \\ 1 \\ 1 \end{array} \right) + r \cdot \left( \begin{array}{} 0 \\ 0 \\ 4 \end{array} \right)
$$
Als Ansatz für den kürzesten Verbindungsvektor $\overrightarrow{PX}$ gilt damit \begin{align} \vec u \cdot \overrightarrow{PX} = 0 \end{align} Mit $\vec u = \left( \begin{array}{} 0 \\ 0 \\ 4 \end{array} \right)$ und $\overrightarrow{PX} = \vec x - \vec p = \left( \begin{array}{} 1 + r \cdot 0 - 2 \\ 1 + r \cdot 0 - 1 \\ 1 + r \cdot 4 - (-1) \end{array} \right)$ folgt für den Ansatz: \begin{align} \left( \begin{array}{} 0 \\ 0 \\ 4 \end{array} \right) \cdot \left( \begin{array}{} 1 + r \cdot 0 - 2 \\ 1 + r \cdot 0 - 1 \\ 1 + r \cdot 4 - (-1) \end{array} \right) &= 0 \\ \\ \left( \begin{array}{} 0 \\ 0 \\ 4 \end{array} \right) \cdot \left( \begin{array}{} -1 \\ 0 \\ 2 + 4r \end{array} \right) &= 0 \\ \\ 0 \cdot (-1) + 0 \cdot 0 + 4 \cdot (2 + 4r) &= 0 \\ \\ 8 + 16 r &= 0 \\ \\ r &= - \frac 12 \end{align} Mit dem Wert für $r$ erhält man den Punkt $X$ der Geraden, der den kürzesten Abstand zum Punkt $P$ hat. Den Ortsvektor des Punktes ist damit: \begin{align} \vec x &= \left( \begin{array}{} 1 \\ 1 \\ 1 \end{array} \right) + \left(- \frac 12 \right) \cdot \left( \begin{array}{} 0 \\ 0 \\ 4 \end{array} \right) \\ \\ \vec x &= \left( \begin{array}{} 1 \\ 1 \\ -1 \end{array} \right) \end{align} Mit dem Abstand $d$ des Punktes von der Geraden folgt: \begin{align} d &= \vert \overrightarrow{PX} \vert \\ \\ d &= \vert \vec x - \vec p \vert \\ \\ d &= \left\vert \left( \begin{array}{} 1 \\ 1 \\ -1 \end{array} \right) - \left( \begin{array}{} 2 \\ 1 \\ -1 \end{array} \right) \right\vert \\ \\ d &= \left\vert \left( \begin{array}{} -1 \\ 0 \\ 0 \end{array} \right) \right\vert \\ \\ d &= \sqrt{(-1)^2} \\ \\ d &= 1 \end{align} Der Abstand beträgt also genau eine Längeneinheit: $d = 1 \text{ LE}$.
© mondbrand MMXIX