Beispielaufgaben

Hier werden Aufgaben vorgestellt und vorgerechnet, die mit den Feldern Häufigkeit - Wahrscheinlichkeit, Baumdiagramme, Mehr-Felder-Tafel und bedingte Wahrscheinlichkeit zu tun haben.

Mail-Überwachung

Eine Behörde überwacht mit Hilfe einer Software die unverschlüsselte E-Mail-Kommunikation deutscher Internetnutzer. Die Software, die die E-Mails auf eine Reihe von Schlüsselbegriffen und -phrasen filtert, die auf illegale und/oder terroristische Aktivitäten hinweisen könnten, stuft eine tatsächlich sicherheitsrelevante Kommunikation mit einer sehr hohen Wahrscheinlichkeit von 99,5% als potentielle Bedrohung ein. Die Wahrscheinlichkeit dafür, dass eine harmlose E-Mail fälschlicherweise als potentielle Bedrohung klassifiziert wird, liegt dagegen nur bei 0,5%.

In Deutschland gibt es ca. 71.000.000 Internetnutzer. Nachfolgend geht man davon aus, dass

• jeder Nutzer täglich zehn unverschlüsselte E-Mails verschickt, die von der Software gesichtet werden
• 10.000 Nutzer das Internet für die Vorbereitung illegaler und/oder terroristischer Aktivitäten nutzen
• jede vierte E-Mail, die von einem dieser 10.000 Nutzer verschickt wird, einen auffindbaren Hinweis auf eine solche Aktivität enthält

Wie groß ist die Wahrscheinlichkeit dafür, dass eine an einem beliebigen Tag durch die Software als potentielle Bedrohung eingestufte E-Mail auch tatsächlich auf eine reale Bedrohungslage hinweist?

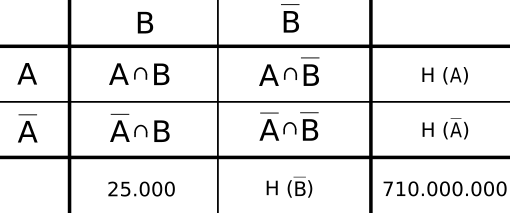
In der gezeigten Mehr-Felder-Tafel werden die Merkmale $B$ (Bedrohung), $\bar B$ (keine Bedrohung), $A$ (aufgespürt) und $\bar A$ (nicht aufgespürt) verwendet. Außerdem werden Häufigkeiten in der Tafel eingetragen.
Jeder Nutzer schreibt täglich zehn Mails, d.h., es geht insgesamt um 710.000.000 Mails. Das ist der Wert unten rechts. Als Bedrohung können 25.000 Mails eingeschätzt werden (10.000 Nutzer, jeder zehn Mails, davon ein Viertel).
Die Software erkennt eine tatsächliche Bedrohung mit einer Wahrscheinlichkeit von 99,5%: $$ A \cap B = 25.000 \cdot 0,995 = 24.875 $$ Insgesamt gibt es 710.000.000 - 25.000 = 709.975.000 harmlose Mails. Eine harmlose Mail wird zu 0,5% als Bedrohung eingestuft: $$ A \cap \bar B = 709.975.000 \cdot 0,005 = 3.549.875 $$ Dann ergeben sich für: $$ \bar A \cap B = 25.000 - 24875 = 125 $$ $$ \bar A \cap \bar B = 709.975.000 - 3.549.875 = 706.425.250 $$ Alle aufgespürten Mails ergeben sich zu 24.875 + 3.549.875 = 3.574.750 und alle nicht aufgespürten Mails entsprechend zu 125 + 706.425.125 = 706.425.250.

Es entsteht die gefüllte Mehr-Felder-Tafel:

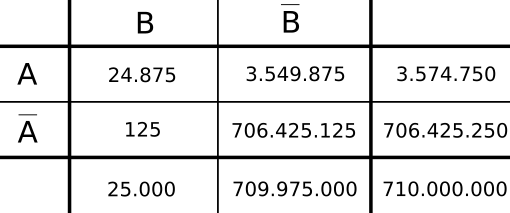
Von den täglich aufgespürten 3.574.750 Mail, die als Bedrohung eingestuft werden, sind nur 24.875 Mails eine tatsächliche Bedrohung. Das sind: $ \frac{24875}{3574750} = 0,007 $ , also etwa 0,7%.

Ebenso ist es natürlich interessant, dass in absoluten Zahlen bei diesem Szenario 125 Mails nicht aufgespührt werden, die eine Bedrohung darstellen können.

© mondbrand MMXIX