

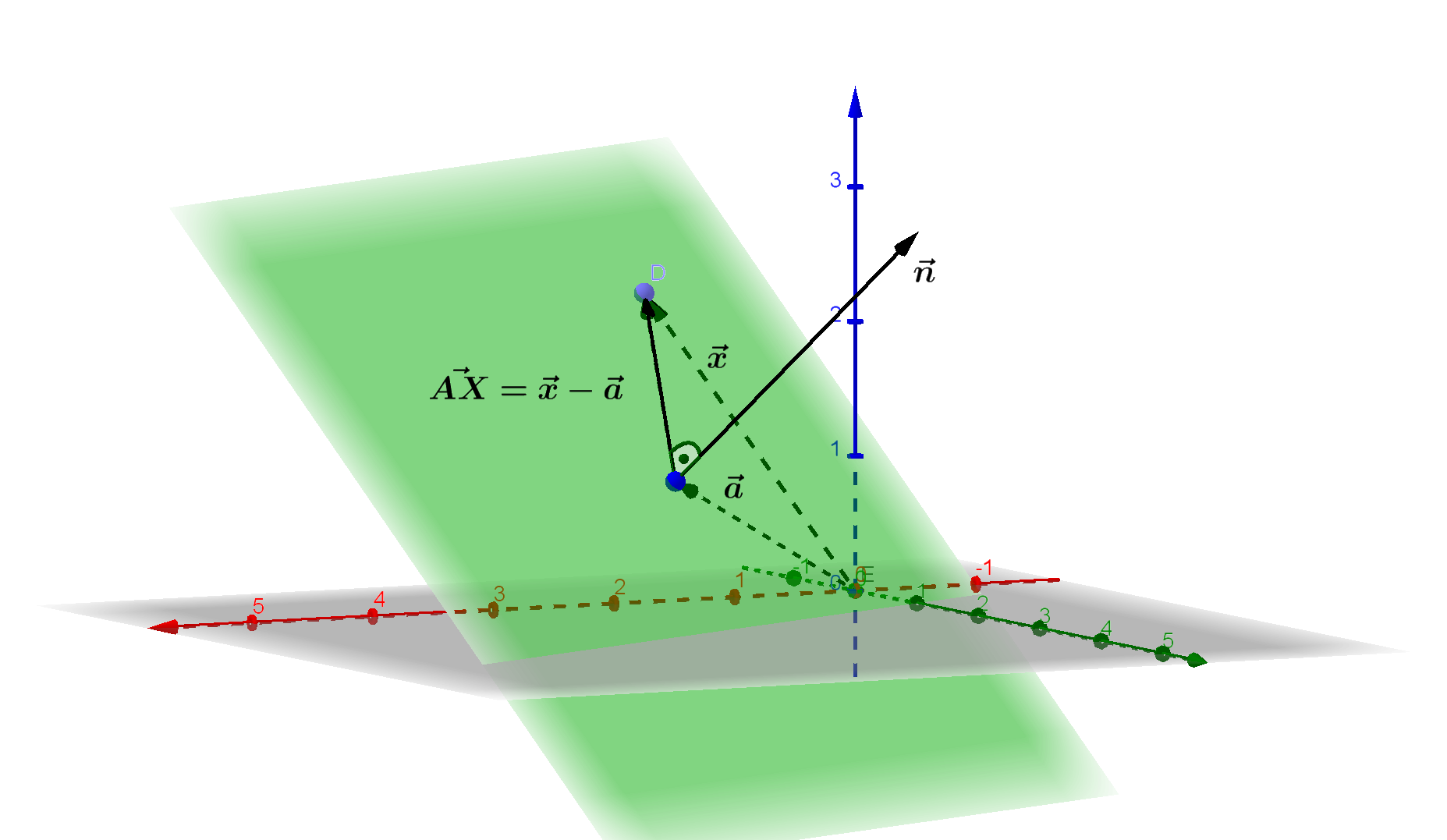
Mit einem Stützpunkt und einem Vektor, der senkrecht (orthogonal) auf der Ebene steht, einem Normalenvektor, kann eine Ebene in der Normalenform definiert werden: $$ \boldsymbol{E: \left( \vec x - \vec a \right) \cdot \vec n = 0} $$ Ein Vektor von einem bekannten Punkt $A$ zu einem beliebigen Punkt $X$ steht senkrecht auf einem Normalenvektor $\vec n$ der Ebene, so dass das Skalarprodukt Null ergibt.
Um den Normalenvektor einer Ebene zu bestimmen, gibt es mehrere Möglichkeiten:
1. Durch die Vektormultiplikation der beiden Richtungsvektoren einer Ebene in Parameterform erhält man einen Vektor, der auf beiden Richtungsvektoren
senkrecht steht: den Normalenvektor.
$$
\vec u \times \vec v = \vec n
$$
2. Die Forderung, dass der Normalenvektor senkrecht zu beiden Richtungsvektoren sein muss, kann auch durch die beiden folgenden Bedingungen erfüllt werden.
\begin{align}
\vec n \cdot \vec u &= 0 \\
\vec n \cdot \vec v &= 0
\end{align}
Aus den beiden Bedingungen entsteht ein Gleichungssystem, das für die unbekannten Größen $n_1$, $n_2$ und $n_3$ gelöst werden muss. Es entsteht:
\begin{align}
n_1 \cdot u_1 + n_2 \cdot u_2 + n_3 \cdot u_3 &= 0 \\
n_1 \cdot v_1 + n_2 \cdot v_2 + n_3 \cdot v_3 &= 0
\end{align}
© mondbrand MMXIX