

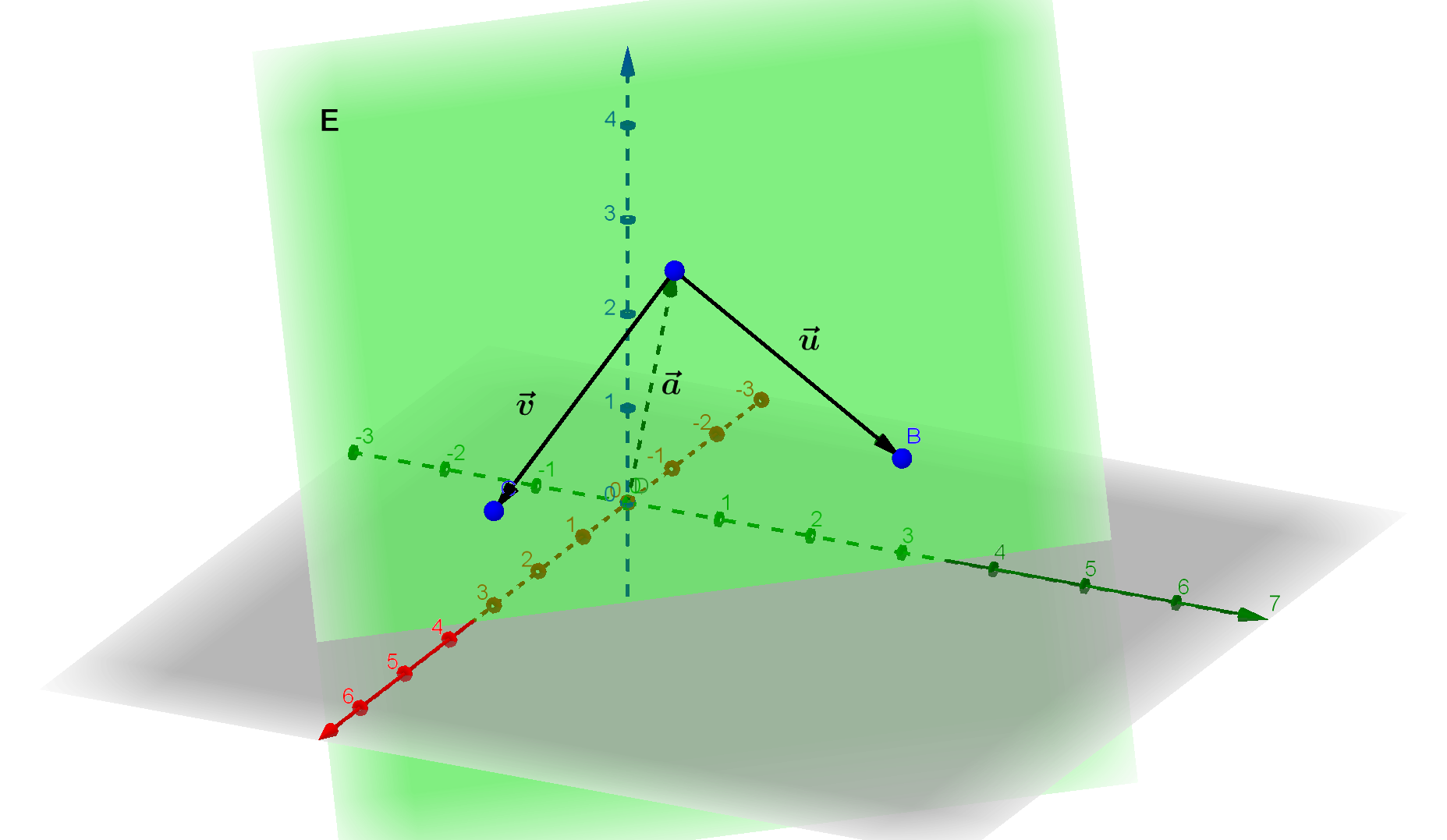
Sind drei Punkte gegeben, lässt sich daraus eine Ebene definieren. Ein Punkt dient als Stützpunkt, zwischen den drei Punkten werden zwei Verbindungsvektoren aufgestellt, die als Richtungsvektoren der Ebene fungieren. $$ \boldsymbol{E: \vec x = \vec a + s \cdot \vec u + t \cdot \vec v} $$ Das ist die Ebenengleichung in der Parameterform mit dem Stützvektor $\boldsymbol{\vec a}$, den Richtungsvektoren $\boldsymbol{\vec u}$ und $\boldsymbol{\vec v}$ und den Parametern $\boldsymbol{s}$ und $\boldsymbol{t}$, für die gilt: $s, t \in \mathbb{R}$.
Die Richtungsvektoren werden folgendermaßen gebildet: \begin{align} \vec u &= \vec{AB} = \vec b - \vec a \\ \vec v &= \vec{AC} = \vec c - \vec a \end{align}
Werden die Richtungsvektoren nicht bestimmt, folgt die Ebenengleichung in der Drei-Punkte-Form: $$ \boldsymbol{E: \vec x = \vec a + s \cdot \left( \vec b - \vec a \right) + t \cdot \left( \vec c - \vec a \right)} $$
© mondbrand MMXIX