


Jeder Punkt $X$ einer Geraden $g$ kann durch seinen Ortsvektor $\vec x$ bestimmt werden. Der Ortsvektor $\vec x$ widerum kann durch den Ortsvektor $\vec a$ eines bekannten Punktes der Geraden, des Stützpunktes, hier: Punkt $A$, und eines Vielfachen eines Richtungsvektors, der entlang der Geraden orientiert ist, $r \cdot \vec u$, angegeben werden. Die Gleichung für die Gerade sieht dann so aus: $$ \boldsymbol{g: \vec x = \vec a + r \cdot \vec u} $$ Das ist die Geradengleichung in der Parameterform mit dem Stützvektor $\boldsymbol{\vec a}$, dem Richtungsvektor $\boldsymbol{\vec u}$ und dem Parameter $\boldsymbol{r}$, für den gilt: $r \in \mathbb{R}$.
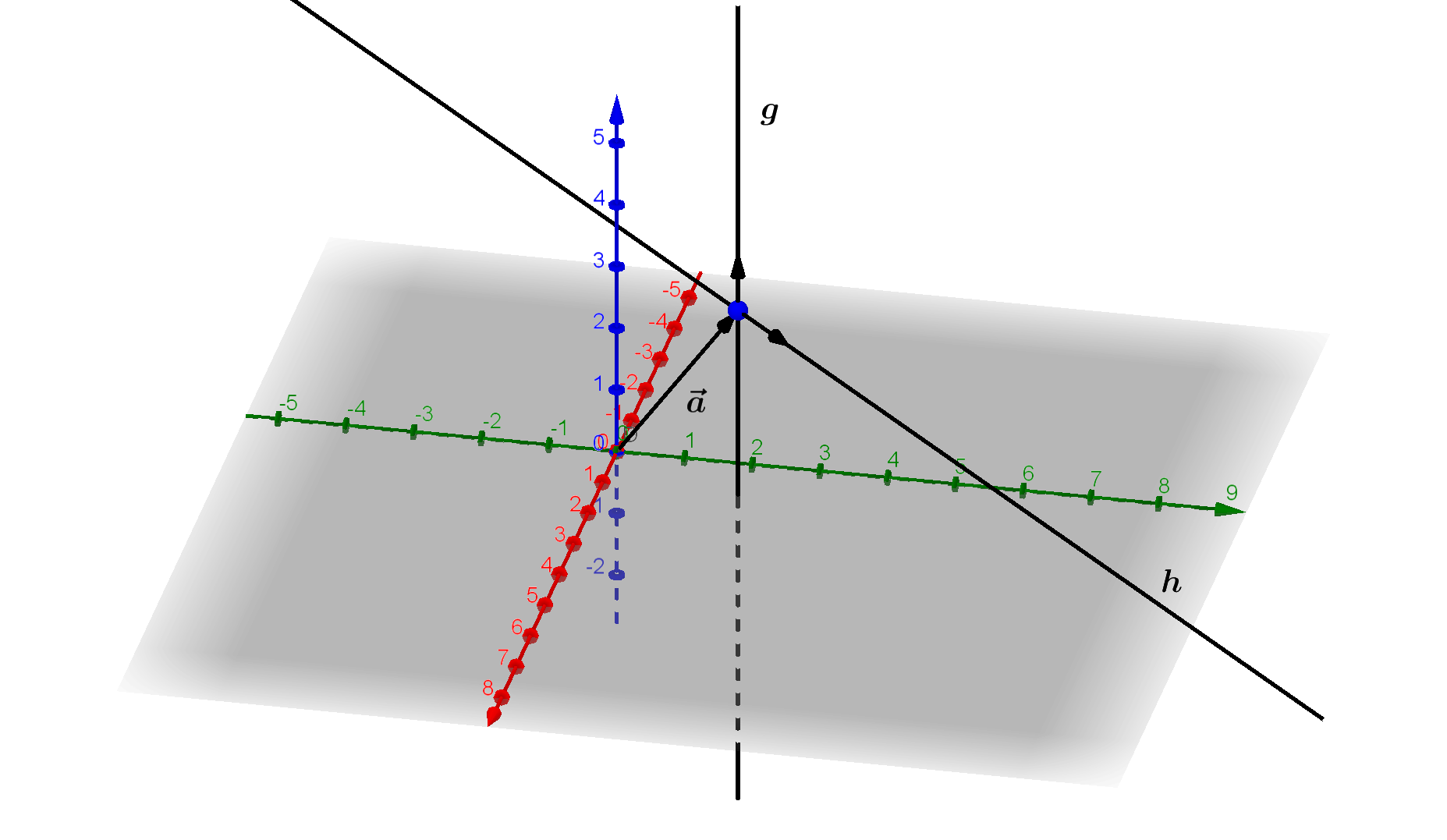
Eine Gerade, deren Richtungsvektor in eine der Koordinatenachsen-Richtungen zeigt, verläuft parallel zu dieser Achse: \begin{align} g: \vec x = \left( \begin{array}{} 1 \\ 2 \\ 3 \end{array} \right) + r \cdot \left( \begin{array}{} 0 \\ 0 \\ 1 \end{array} \right) \end{align}
Mit einem Richtungsvektor, der als eine der Komponenten eine Null hat, verläuft eine Gerade parallel zu einer der Koordinatenebenen: \begin{align} h: \vec x = \left( \begin{array}{} 1 \\ 2 \\ 3 \end{array} \right) + r \cdot \left( \begin{array}{} 1 \\ 1 \\ 0 \end{array} \right) \end{align}
Insbesondere lauten die Geradengleichungen für die Koordinatenachsen: \begin{align} x_1-Achse: \vec x = \left( \begin{array}{} a_1 \\ 0 \\ 0 \end{array} \right) + r \cdot \left( \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right) \\ \\ x_2-Achse: \vec x = \left( \begin{array}{} 0 \\ a_2 \\ 0 \end{array} \right) + r \cdot \left( \begin{array}{} 0 \\ 1 \\ 0 \end{array} \right) \\ \\ x_3-Achse: \vec x = \left( \begin{array}{} 0 \\ 0 \\ a_3 \end{array} \right) + r \cdot \left( \begin{array}{} 0 \\ 0 \\ 1 \end{array} \right) \end{align}
© mondbrand MMXIX