Der LC-Kreis besteht aus einem Kondensator und einer Spule. Zunächst wird, wie in der Abbildung gezeigt, der Kondensator durch die
äußere Spannung $U_0$ aufgeladen.
(siehe dazu: Der RC-Kreis)
Der Kondensator hat nun also nach einer bestimmten Zeit die Spannung $U_C = U_0$. Der Schalter wird in die andere Position gebracht, so dass
die Spannungsquelle keine Rolle mehr spielt. Der Kreis besteht nur noch aus dem Kondensator und der Spule.
Der Kondensator ist geladen und es existiert ein elektrisches Feld zwischen den Kondensatorplatten. Die gesamte Energie des Systems ist in diesem elektrischen Feld gespeichert. Es gilt: $E_{max} = \frac{1}{2} C U^2$.
Die negativen Ladungen (Elektronen), die sich auf der negativen Seite des Kondensators befinden, streben jetzt den Ladungsausgleich an, und bewegen sich durch den Leiter und durch die Spule zu der anderen, positiven Kondensatorseite.
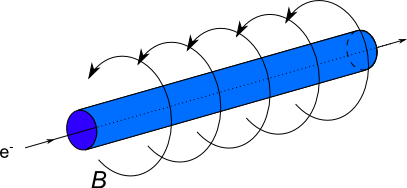Jeder stromdurchflossene Leiter baut um sich herum ein magnetisches Wirbelfeld auf. Beim Durchgang durch die Spule werden die einzelnen
Wirbelfelder jedes Leiterstücks überlagert und es entsteht so innerhalb der Spule ein
nahezu homogenes Magnetfeld.
Insgesamt entsteht ein Feld, wie es etwa in der Abbildung zu sehen ist.
Die Bildung des Magnetfelds führt natürlich dazu, dass sich in der Spule der magnetische Fluss $\Phi$ ändert. Mit dem Induktionsgesetz $$ U_{Ind} = - N \cdot \frac{d \Phi}{dt} $$ wird eine Induktionsspannung erzeugt, die nach der Lenz'schen Regel der äußeren Spannung $U_0$ bzw. $U_C$ entgegengesetzt ist.
Da die Änderung des magnetischen Flusses am Anfang immer maximal ist und im zeitlichen Verlauf abnimmt, bis der Fluss selbst maximal und seine Änderung Null ist, ist die Induktionsspannung zu Beginn auch maximal, nimmt dann ab bis Null, so dass durch die Spule der maximale Strom fließt. Maximaler Fluss bedeutet auch, dass das Magnetfeld am stärksten ist. In diesem Zusatnd ist die Systemenergie im Magnetfeld gespeichert, $E_{max} = \frac{1}{2} L I^2$.
In diesem Zustand wäre der Prozess eigentlich zu Ende, da zwischen den beiden Kondensatorplatten ein Ladungsausgleich bestünde. Da aber die Stromstärke nicht abrupt vom Maximalwert auf Null fallen kann, sondern mehr oder weniger langsam abgebaut werden muss, heißt dass, dass die Stromstärke langsam abnimmt, wodurch das Magnetfeld schwächer wird. Durch die Änderung des Magnetfeldes entsteht widerum eine Induktionsspannung, die dafür sorgt, dass die Abnahme der Stromstärke abgeschwächt wird. Der Prozess dauert dann so lange an, bis die Stromstärke durch die Spule Null und das Magnetfeld um die Spule verschwunden ist.
Durch den nach dem Gleichgewicht trotzdem stattfindenen Stromfluss sammeln sich die Elektronen jetzt auf der zweiten Kondensatorplatte an, und es entsteht ein elektrisches Feld, was dem ersten elektrischen Feld entgegengesetzt orientiert ist. Die Energie des Systems ist wieder im elektrischen Feld gespeichert. Die Elektronen werden wieder den Ladungsausgleich anstreben und sich in Richtung der positiven Kondensatorplatte bewegen, wodurch sie wieder ein Magnetfeld um die Spule herum erzeugen, dessen Orientierung der des ersten Magnetfeldes entgegengesetzt ist. Der Prozess wiederholt sich also.
Die maximalen Energien, die im elektrischen Feld und im magnetischen Feld gespeichert sind, sind gleich groß, allerdings nicht gleichzeitig. Vielmehr ist es so, dass zum Zeitpunkt der maximalen elektrischen Energie die magnetische Energie gerade Null ist und umgekehrt. Zu jedem beliebigen Zeitpunkt gilt allerdings: $$ E_{Ges} = E_{el}(t) + E_{mag}(t) $$ Die zeitabhängige Größe bei der elektrischen Energie ist die Spannung $U$, also $U(t)$, und bei der magnetischen Energie die Stromstärke $I$, also $I(t)$. Für die Gesamtenergie gilt somit zu jedem Zeitpunkt: $$ E_{Ges} = \frac12 C U^2(t) + \frac12 L I^2(t) = konstant $$ Für die Spannung am Kondensator lässt sich schreiben: $U(t) = \frac{Q(t)}{C}$. Und für die Stromstärke gilt: $I(t) = \frac{dQ(t)}{dt} = Q'(t)$. Insgesamt folgt für die Gesamtenergie: $$ E_{Ges} = \frac12 \frac{Q^2(t)}{C} + \frac12 L Q'^{\,2}(t) = konstant $$ Nun wird ausgenutzt, dass sich die Gesamtenergie nicht ändert (reibungsloser Fall). Damit gilt $\frac{dE}{dt} = 0$ und \begin{align} \frac{d \left( \frac12 \frac{Q^2(t)}{C} \right)}{dt} + \frac{d \left( \frac12 L Q'^{\,2}(t) \right)}{dt} &= 0 \\ \\ \frac{1}{2C} \frac{d Q^2(t)}{dt} + \frac{L}{2} \frac{d Q'^{\,2}(t)}{dt} &= 0 \end{align} Bei den jeweiligen Ableitungen, also der Ableitung von $Q$ nach der Zeit und der Ableitung von $Q'$ nach der Zeit, ist zu beachten, dass die Größen im Quadrat vorhanden sind, also etwa so: $\frac{d Q^2(t)}{dt} = \frac{d \left( Q(t) \cdot Q(t) \right)}{dt}$ und $\frac{d Q'^{\,2}(t)}{dt} = \frac{d \left( Q'(t) \cdot Q'(t) \right)}{dt}$. Für die Ableitung muss also die Produktregel angewendet werden. Das führt dann für die zeitabhängigen Größen $Q$ und $Q'$ zu den folgenden Termen: \begin{align} \frac{d \left( Q(t) \cdot Q(t) \right)}{dt} &= Q'(t) \cdot Q(t) + Q(t) \cdot Q'(t) \\ \\ &= 2 Q(t)Q'(t) \end{align} und \begin{align} \frac{d \left( Q'(t) \cdot Q'(t) \right)}{dt} &= Q''(t) \cdot Q'(t) + Q'(t) \cdot Q''(t) \\ \\ &= 2 Q'(t)Q''(t) \end{align} Damit folgt für $\frac{dE}{dt} = 0$: \begin{align} \frac{1}{2C} \frac{d Q^2(t)}{dt} + \frac{L}{2} \frac{d Q'^{\,2}(t)}{dt} &= 0 \\ \\ \frac{1}{2C} \cdot 2 Q(t)Q'(t) + \frac{L}{2} \cdot 2 Q'(t)Q''(t) &= 0 \\ \\ \frac{1}{C} Q(t)Q'(t) + L Q'(t)Q''(t) &= 0 \\ \\ Q'(t) \left(\frac{1}{C} Q(t) + L Q''(t) \right) &= 0 \end{align} Der Term $Q'(t)$ ist nicht die ganze Zeit gleich Null, also muss der Klammerausdruck gleich Null sein. \begin{align} \frac{1}{C} Q(t) + L Q''(t) &= 0 \\ \\ Q''(t) &= - \frac{1}{LC} Q(t) \end{align} Diese Differentialgleichung kann mit dem folgenden Ansatz gelöst werden: \begin{align} Q(t) &= \sin(\omega t) \\ \\ Q'(t) &= \omega \cdot \cos (\omega t) \\ \\ Q''(t) &= - \omega^2 \cdot \sin ( \omega t) \end{align} Aus dem Vergleich der beiden Terme für $Q''$ folgt $\omega = \frac{1}{\sqrt{LC}}$ und wegen $\omega = \frac{2 \pi}{T}$ für die Periodendauer $T = 2 \pi \sqrt{LC}$ bzw. für die Frequenz $f = \frac{1}{2 \pi \sqrt{LC}}$ (Eigenfrequenz $f_0$ des Schwingkreises).
Der Gesamtprozess entspricht einer Schwingungsbewegung von Elektronen (Ladungen) von einer Kondensatorplatte zur anderen, wobei der Durchfluss durch die Spule dem Durchgang durch die Gleichgewichtsposition bei der mechanischen Schwingung entspricht. Da der Prozess durch die (reibungsbehaftete) Bewegung der Elektronen gekennzeichnet ist, muss Energie zugeführt werden, damit er nicht zum Erliegen kommt. Im Unterschied zu den mechanischen Schwingungen ist hier aber die Schwingungsgleichung $Q(t)$ von untergeordnetem Interesse. Wichtig ist vielmehr die Eigenfrequenz des Schwingkreises: $$ f_0 = \frac{1}{2 \pi \sqrt{LC}} $$
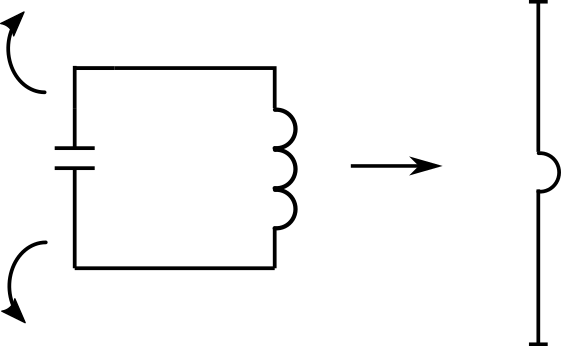Der Schwingkreis kann nun virtuell aufgebogen werden, so dass die beiden Kondensatorplatten die Enden eines langes Stabes bilden.
Der Stab selbst entspricht dann in etwa der Spule.
Der sogenannte Hertzsche Dipol hat gegenüber einem Kondensator und gegenüber einer Spule deutlich geringere Werte für Kapazität und Induktivität. Das hat zur Folge, dass die Eigenfrequenz des Schwingkreises von etwa 10 - 100 Hz auf Werte im Bereich von etwa 100 MHz ansteigen kann.
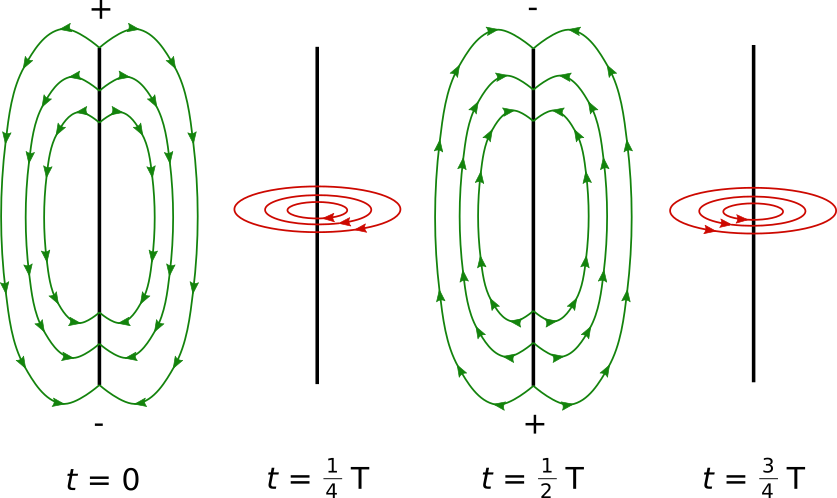Während jeder Schwingungsperiode wird also zunächst ein elektrisches Feld erzeugt $(t = 0)$, anschließend ein magnetisches Feld $(t = \frac{1}{4}T)$, dann wieder
ein elektrisches Feld $(t = \frac{1}{2}T)$ und schließlich wieder ein magnetisches Feld $(t = \frac{3}{4}T)$. Zum Zeitpunkt $t = T$ wird wieder ein
elektrisches Feld wie bei $t = 0$ erzeugt.
In der Abbildung ist eine Darstellung der Felder gezeigt.
Die Abfolge der elektrischen- und der magnetischen Feldstärke kann auch als stehende Welle für die Spannung zwischen den Dipolenden
(elektrische Feldstärke) und der Stromstärke in der Mitte des Dipols (magnetische Feldstärke) aufgefasst werden. Die Darstellung sieht dann etwa
so aus:
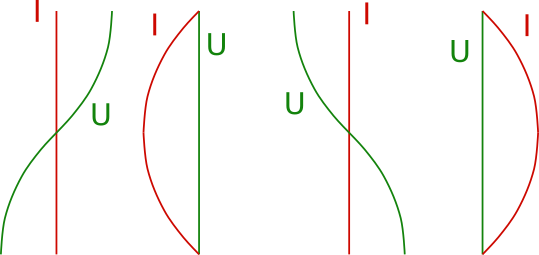
Die Spannung ist damit in der Mitte des Dipols immer gleich Null. Entsprechend ist an der Enden des Dipols die Stromstärke immer gleich Null.
Wenn das jeweilige Feld erst erzeugt und dann wieder abgebaut wird, kommt es zu einer Abschnürung der Feldlinien. Damit lösen sich die Felder
von dem Dipol und bewegen sich von dem Dipol weg durch den Raum. Die Felder werden vom Dipol abgestrahlt.
Hier muss jetzt unterschieden werden zwischen dem Bereich in unmittelbarer Nähe zum Dipol und dem Bereich in weiter Entfernung vom Dipol. In der
Nähe des Dipols besteht zwischen den abgestrahlten Feldern eine Phasendifferenz von $\frac{\pi}{2}$ gemäß der Theorie bei der Erzeugung der Felder
(Nahfeld). In
größerer Entfernung allerdings befinden sich die Felder in Phase. Die elektrische und die magnetische Feldstärke schwingen ohne Phasenunterschied und
sind dementsprechend zur selben Zeit maximal und zur selben Zeit Null (Fernfeld).
Im Zuge der Betrachtung der Induktion ergab sich ein Zusammenhang zwischen elektrischer und magnetischer Feldstärke und der Bewegungsgeschwindigkeit der Felder: $E = v \cdot B$.
Um die Geschwindigkeit $v$ zu bestimmen, werden die Feldenergien betrachtet. \begin{align} W_{el} &= \frac12 \cdot C \cdot U^2 \qquad &\qquad W_{mag} &= \frac12 \cdot L \cdot I^2 \\ \\ \end{align} Für die Größen Kapazität und Eigeninduktivität gelten die folgenden Gleichungen: \begin{align} C &= \epsilon_0 \cdot \epsilon_r \cdot \frac{A}{d} \qquad &\qquad L &= \mu_0 \cdot \mu_r \cdot N^2 \cdot \frac{A}{l} \\ \\ \end{align} Damit ergeben sich: \begin{align} W_{el} &= \frac12 \cdot \epsilon_0 \cdot \epsilon_r \cdot \frac{A}{d} \cdot U^2 \qquad &\qquad W_{mag} &= \frac12 \cdot \mu_0 \cdot \mu_r \cdot N^2 \cdot \frac{A}{l} \cdot I^2 \\ \\ \end{align} Die Zusammenhänge zwischen Spannung und elektrischer Feldstärke sowie zwischen Stromstärke und magnetischer Flussdichte führen zu: \begin{align} E &= \frac{U}{d} \qquad &\qquad B &= \mu_0 \cdot \mu_r \cdot I \cdot \frac{N}{l} \\ \\ U^2 &= E^2 \cdot d^2 \qquad &\qquad I^2 &= \frac{B^2 \cdot l^2}{\mu_0^2 \cdot \mu_r^2 \cdot N^2} \end{align} Damit ergeben sich die folgenden Gleichungen: \begin{align} W_{el} &= \frac12 \cdot \epsilon_0 \cdot \epsilon_r \cdot \frac{A}{d} \cdot E^2 \cdot d^2 \qquad &\qquad W_{mag} &= \frac12 \cdot \mu_0 \cdot \mu_r \cdot N^2 \cdot \frac{A}{l} \cdot \frac{B^2 \cdot l^2}{\mu_0^2 \cdot \mu_r^2 \cdot N^2} \\ \\ W_{el} &= \frac12 \cdot \epsilon_0 \cdot \epsilon_r \cdot E^2 \cdot A \cdot d \qquad &\qquad W_{mag} &= \frac{1}{2 \cdot \mu_0 \cdot \mu_r} \cdot B^2 \cdot A \cdot l \end{align} In der Dipolanordnung entsprechen sich die beiden Volumina des Raums, in dem das elektrische Feld wirkt $(A \cdot d)$ und in dem das magnetische Feld wirkt $(A \cdot l)$. Mit der Annahme der gleichen Volumina und der gleichen Feldenergie folgt \begin{align} \frac12 \cdot \epsilon_0 \cdot \epsilon_r \cdot E^2 &= \frac{1}{2 \cdot \mu_0 \cdot \mu_r} \cdot B^2 \\ \\ E^2 &= \frac{1}{\epsilon_0 \cdot \epsilon_r \cdot \mu_0 \cdot \mu_r} \cdot B^2 \\ \\ E^2 &= c^2 \cdot B^2 \end{align} $c$ ist die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle. Es gilt also: $$ c = \frac{1}{\sqrt{\epsilon_0 \cdot \epsilon_r \cdot \mu_0 \cdot \mu_r}} $$ Im Vakuum sind $\epsilon_r = 1$ und $\mu_r = 1$. Damit folgt für die Ausbreitungsgeschwindigkeit der elektromagnetischen Welle im Vakuum: $$ c_0 = \frac{1}{\sqrt{\epsilon_0 \cdot \mu_0}} $$ Es ist somit \begin{align} c_0 &= \frac{1}{\sqrt{\epsilon_0 \cdot \mu_0}} \\ \\ c_0 &= \frac{1}{\sqrt{8,854187817 \cdot 10^{-12} \, \frac{\text{As}}{\text{Vm}} \cdot 4 \cdot \pi \cdot 10^{-7} \, \frac{\text{N}}{\text{A}^2}}} \\ \\ c_0 &= 299792458 \, \frac{\text{m}}{\text{s}} \end{align} Das entspricht der definierten Lichtgeschwindigkeit $c_0 = 299792458 \, \frac{\text{m}}{\text{s}}$. Damit war klar, dass Licht eine elektromagnetische Welle ist.
© mondbrand MMXIX