Das Skalarprodukt

Geometrische Definition

Das Skalarprodukt zweier Vektoren $\vec a$ und $\vec b$ lautet: $$ \mathbf{\vec a \cdot \vec b = \lvert \vec a \rvert \cdot \lvert \vec b \rvert \cdot \cos \alpha} $$

Zur Bestimmung des Skalarprodukts werden also die Beträge der beiden Vektoren und der Winkel zwischen den Vektoren benötigt.
Mit der Bestimmungsformel wird sofort klar, dass das Skalarprodukt Null ergibt, wenn der Winkel genau 90° beträgt. Damit bekommt man eine Möglichkeit, zwei Vektoren auf ihre Orthogonalität zu untersuchen:

$\rightarrow \quad$ Zwei Vektoren sind genau dann orthogonal zueinander, wenn ihr Skalarprodukt Null ergibt.

$\rightarrow \quad$ Wenn das Skalarprodukt zweier Vektoren Null ergibt, dann sind die beiden Vektoren orthogonal zueinander.

Wenn man den Vektor $\vec a$ zerlegt in einen Anteil, der parallel zu $\vec b$ verläuft und einen Anteil, der senkrecht auf $\vec b$ steht, erhält man das folgende Bild:

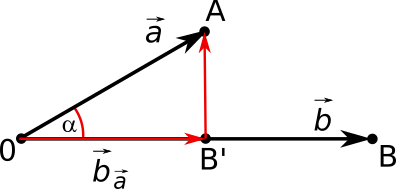
Es gilt also: $\vec a = \vec b_{\vec a} + \vec{B'A}$. Damit kann das Skalarprodukt folgendermaßen geschrieben werden: \begin{align} \vec a \cdot \vec b &= \left( \vec b_{\vec a} + \vec {B'A} \right) \cdot \vec b \\ \\ \vec a \cdot \vec b &= \vec b_{\vec a} \cdot \vec b + \vec {B'A} \cdot \vec b \\ \\ \vec a \cdot \vec b &= \vec b_{\vec a} \cdot \vec b \end{align} $\vec {B'A} \cdot \vec b = 0$, da beide Vektoren senkrecht, also orthogonal zueinander stehen. Aus der letzten Gleichung folgt mit der Definitionsgleichung des Skalarprodukts: \begin{align} \vec a \cdot \vec b &= \vec b_{\vec a} \cdot \vec b \\ \vec a \cdot \vec b &= \lvert \vec b_{\vec a} \rvert \cdot \lvert \vec b \rvert \cdot \cos \alpha \\ \\ \vec a \cdot \vec b &= \lvert \vec b_{\vec a} \rvert \cdot \lvert \vec b \rvert \end{align} Hier gilt $\cos \alpha = 1$, da beide Vektoren parallel zueinander sind.

Das Skalarprodukt zweier Vektoren $\vec a$ und $\vec b$ ist das Produkt der Länge (des Betrags) des Vektors $\vec b$ und der Länge der Projektion des Vektors $\vec a$ auf die Richtung des Vektors $\vec b$, $\vec b_{\vec a}$.
Mit $\lvert \vec b_{\vec a} \rvert = \lvert \vec a \rvert \cdot \cos \alpha$ folgt die Formulierung von ganz oben: $\vec a \cdot \vec b = \lvert \vec a \rvert \cdot \lvert \vec b \rvert \cdot \cos \alpha$.
Anwendung findet diese Formulierung unter anderem in der Physik. So kann z.B. die mechanischen Arbeit $\left( W = \vec F \cdot \vec s \right)$ mit dem Skalarprodukt berechnet werden (...der Anteil der Kraft in Weg-Richtung...).

Definition im kartesischen Koordinatensystem

Im kartesischen Koordinatensystem gilt, dass jeder Vektor $\vec a$ zusammengesetzt werden kann aus den Längen des Vektors in der Richtung der jeweiligen Koordinatenachse multipliziert mit dem Einheitsvektor in dieser Richtung. Es gilt also: \begin{align} \vec a &= a_1 \cdot \vec x_{1,0} + a_2 \cdot \vec x_{2,0} + a_3 \cdot \vec x_{3,0} \\ \\ \vec a &= a_1 \cdot \left( \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right) + a_2 \cdot \left( \begin{array}{} 0 \\ 1 \\ 0 \end{array} \right) + a_3 \cdot \left( \begin{array}{} 0 \\ 0 \\ 1 \end{array} \right) \\ \\ \vec a &= \vec a_1 + \vec a_2 + \vec a_3 \\ \\ \vec a &= \left( \begin{array}{} a_1 \\ a_2 \\ a_3 \end{array} \right) \end{align} Dies vorausgesetzt, erhält man für das Skalarprodukt die folgende Notation: \begin{align} \vec a \cdot \vec b =& \left( a_1 \cdot \vec x_{1,0} + a_2 \cdot \vec x_{2,0} + a_3 \cdot \vec x_{3,0} \right) \cdot \left( b_1 \cdot \vec x_{1,0} + b_2 \cdot \vec x_{2,0} + b_3 \cdot \vec x_{3,0} \right) \\ \\ \vec a \cdot \vec b =& a_1 \cdot b_1 \cdot \vec x_{1,0} \cdot \vec x_{1,0} + a_1 \cdot b_2 \cdot \vec x_{1,0} \cdot \vec x_{2,0} + a_1 \cdot b_3 \cdot \vec x_{1,0} \cdot \vec x_{3,0} \\ +& a_2 \cdot b_1 \cdot \vec x_{2,0} \cdot \vec x_{1,0} + a_2 \cdot b_2 \cdot \vec x_{2,0} \cdot \vec x_{2,0} + a_2 \cdot b_3 \cdot \vec x_{2,0} \cdot \vec x_{3,0} \\ +& a_3 \cdot b_1 \cdot \vec x_{3,0} \cdot \vec x_{1,0} + a_3 \cdot b_2 \cdot \vec x_{3,0} \cdot \vec x_{2,0} + a_3 \cdot b_3 \cdot \vec x_{3,0} \cdot \vec x_{3,0} \end{align} Da die Richtungseinheitsvektoren $\vec x_{1,0}$, $\vec x_{2,0}$ und $\vec x_{3,0}$ jeweils paarweise orthogonal sind, und damit das Skalaraprodukt jeweils Null ergibt, vereinfacht sich der Ausdruck erheblich: \begin{align} \vec a \cdot \vec b = a_1 \cdot b_1 \cdot \vec x_{1,0} \cdot \vec x_{1,0} + a_2 \cdot b_2 \cdot \vec x_{2,0} \cdot \vec x_{2,0} + a_3 \cdot b_3 \cdot \vec x_{3,0} \cdot \vec x_{3,0} \end{align} Der Ausdruck wird nochmal vereinfacht, da das Skalarprodukt der Richtungseinheitsvektoren mit sich selbst Eins ergibt: \begin{align} \mathbf{\vec a \cdot \vec b = a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3} \end{align} Damit hat man eine Berechnungsvorschrift für das Skalarprodukt der beiden Vektoren $\vec a$ und $\vec b$.

Winkel zwischen Vektoren

Für die Bestimmung des Winkels, der zwischen zwei Vektoren aufgespannt wird, muss lediglich die Definitionsgleichung für das Skalarprodukt umgestellt werden: \begin{align} \vec a \cdot \vec b &= \lvert \vec a \rvert \cdot \lvert \vec b \rvert \cdot \cos \alpha \\ \\ \cos \alpha &= \frac{\vec a \cdot \vec b}{\lvert \vec a \rvert \cdot \lvert \vec b \rvert} \\ \\ \alpha &= \arccos \left( \frac{\vec a \cdot \vec b}{\lvert \vec a \rvert \cdot \lvert \vec b \rvert} \right) \end{align}

Zusammenfassung

\begin{align} \vec a \cdot \vec b &= \lvert \vec a \rvert \cdot \lvert \vec b \rvert \cdot \cos \alpha \\ \\ \vec a \cdot \vec b &= \lvert \vec b_{\vec a} \rvert \cdot \lvert \vec b \rvert \\ \\ \vec a \cdot \vec b &= a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3 \\ \\ \alpha &= \arccos \left( \frac{\vec a \cdot \vec b}{\lvert \vec a \rvert \cdot \lvert \vec b \rvert} \right) \\ \\ \vec a \cdot \vec b &= 0 \qquad \Longleftrightarrow \qquad \vec a \perp \vec b \end{align}

© mondbrand MMXIX