

Differentialgleichungen (Dgl.) sind eine besondere Form von Gleichungen, in denen neben der Größe selbst (z.B. den Bestand) auch deren Veränderung
(z.B. die Ableitung nach der Zeit) vorkommt.
Aus der Tatsache folgt, dass die Gleichungen keine Zahlen oder Werte als Lösungen besitzen, sondern Funktionen.
Es gibt eine Vielzahl von Differentialgleichungen, die die unterschiedlichsten Probleme beschreiben. Ganz wichtige Dgl. sind z.B. diejenigen, die in der Form $$ y' = f(x) \cdot y + g(x) $$ vorliegen. Durch sie werden z.B. natürliche Wachstumsprozesse beschrieben. Diese Dgl. heißen lineare Differentialgleichungen. Im Fall, dass $g(x) = 0$ gilt, heißen sie lineare, homogene Dgl, sonst lineare, inhomogene Dgl.
Für diese Form der Dgl. gibt es verschiedene Lösungsverfahren, von denen hier eins vorgestellt werden soll.
Zunächst wird eine Funktion $y_h$ definiert:
$$
y_h = e^{\int{f(x)dx}}
$$
Dann wird eine Funktion $y_p$ definiert:
$$
y_p = y_h \cdot \int {\frac{g(x)}{y_h}dx}
$$
Dann ist die Lösungsfunktion
$$
y = K \cdot y_h + y_p
$$
Handelt es sich nur um eine homogene Dgl., entfällt der Term $y_p$. Die Konstante $K$ ergibt sich aus den Anfangsbedingungen für die Funktion $y$.
Für das Laden eines Kondensators gilt die Gleichung für die Speisespannung $U_0$: $$ U_0 = R \cdot \frac{\Delta Q}{\Delta t} + \frac{1}{C} \cdot Q $$ Umgestellt nach $\frac{\Delta Q}{\Delta t}$ folgt: $$ \frac{\Delta Q}{\Delta t} = - \frac{1}{RC} \cdot Q + \frac{U_0}{R} $$ Damit erhält man für die Terme $f(x)$ und $g(x)$: $$ f(x) = - \frac{1}{RC} \\ g(x) = \frac{U_0}{R} $$ Für die beiden Funktionen $y_h$ und $y_p$ ergeben sich die folgenden Ausdrücke: $$ y_h = e^{- \frac{t}{RC}} \\ y_p = e^{- \frac{t}{RC}} \cdot \frac{U_0}{R} \cdot RC \cdot e^{\frac{t}{RC}} \\ y_p = U_0 C $$ Damit folgt für die Gesamtfunktion der Ladung: $$ Q(t) = K \cdot e^{- \frac{t}{RC}} + U_0 C $$ Die Anfangsbedingung für den Ladevorgang ist so, dass die Ladung $Q(t) = 0$ ist für $t = 0$. Man erhält also \begin{align} 0 &= K + U_0 C \\ K &= - U_0 C \end{align} Damit bekommt man als Lösung der DGl. \begin{align} Q(t) &= U_0 C - U_0 C e^{- \frac{t}{RC}} \\ \\ Q(t) &= U_0 C \left( 1 - e^{- \frac{t}{RC}} \right) \end{align}
Der Graph sieht dann beispielsweise so aus:
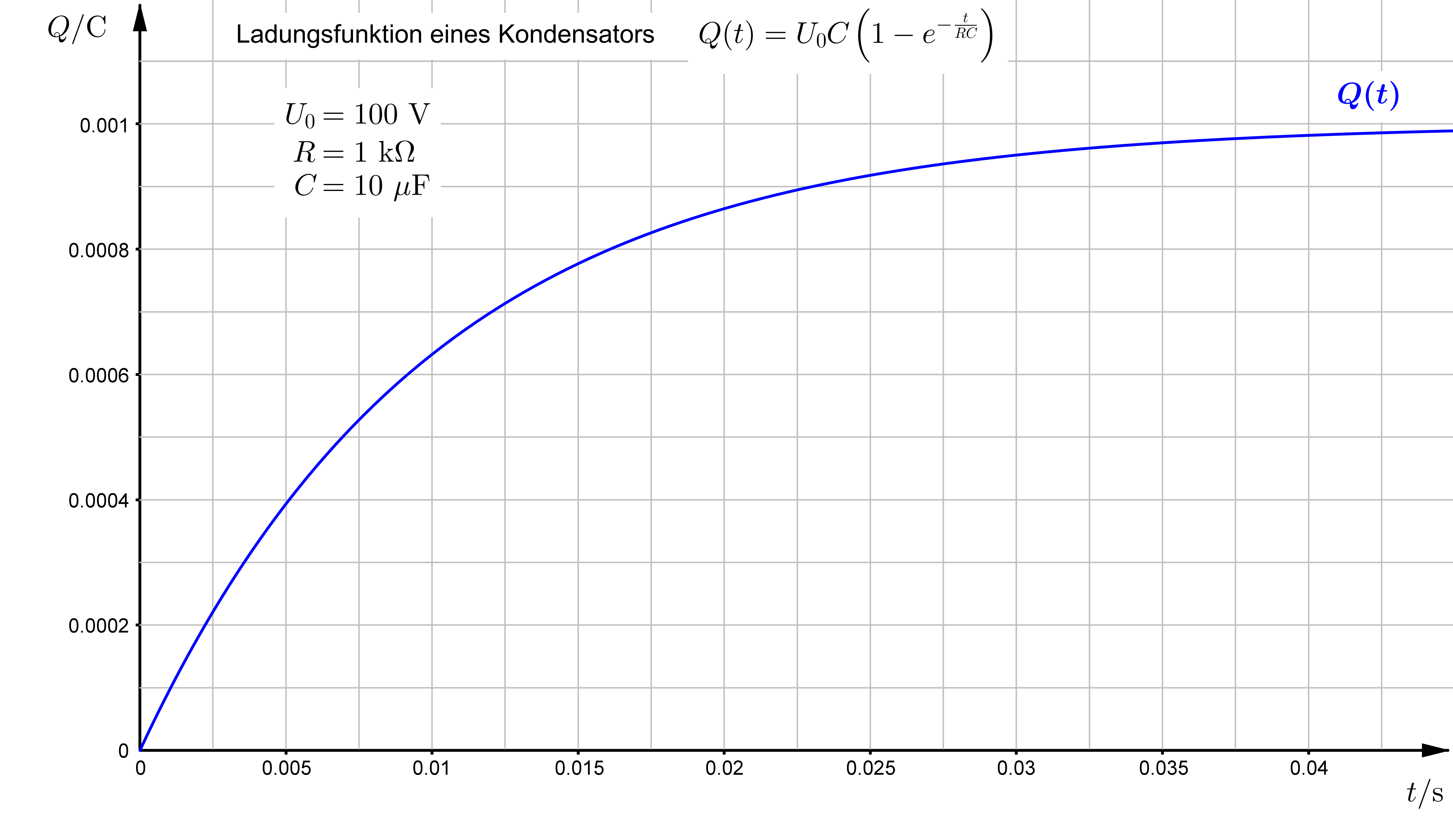
Für das Entladen eines Kondensators gilt ebenso die Gleichung:
$$
\frac{\Delta Q}{\Delta t} = - \frac{1}{RC} \cdot Q + \frac{U_0}{R}
$$
Bei der Entladung ist es allerdings so, dass durch die Spannung $U_0$ der Kondensator nicht mehr aufgeladen wird. Es gilt somit
$U_0 = 0$.
Damit erhält man für die Terme $f(x)$ und $g(x)$:
$$
f(x) = - \frac{1}{RC} \\
g(x) = 0
$$
Für die beiden Funktionen $y_h$ und $y_p$ ergeben sich die folgenden Ausdrücke:
$$
y_h = e^{- \frac{t}{RC}} \\
y_p = 0
$$
Damit folgt für die Gesamtfunktion der Ladung:
$$
Q(t) = K \cdot e^{- \frac{t}{RC}}
$$
Die Anfangsbedingung für den Entladevorgang ist so, dass die Ladung $Q(t) = Q_0$ ist für $t = 0$. Man erhält also
\begin{align}
K &= Q_0
\end{align}
Damit bekommt man als Lösung der DGl.
\begin{align}
Q(t) &= Q_0 \cdot e^{- \frac{t}{RC}} \\ \\
\end{align}
Hier sieht der Graph folgendermaßen aus:
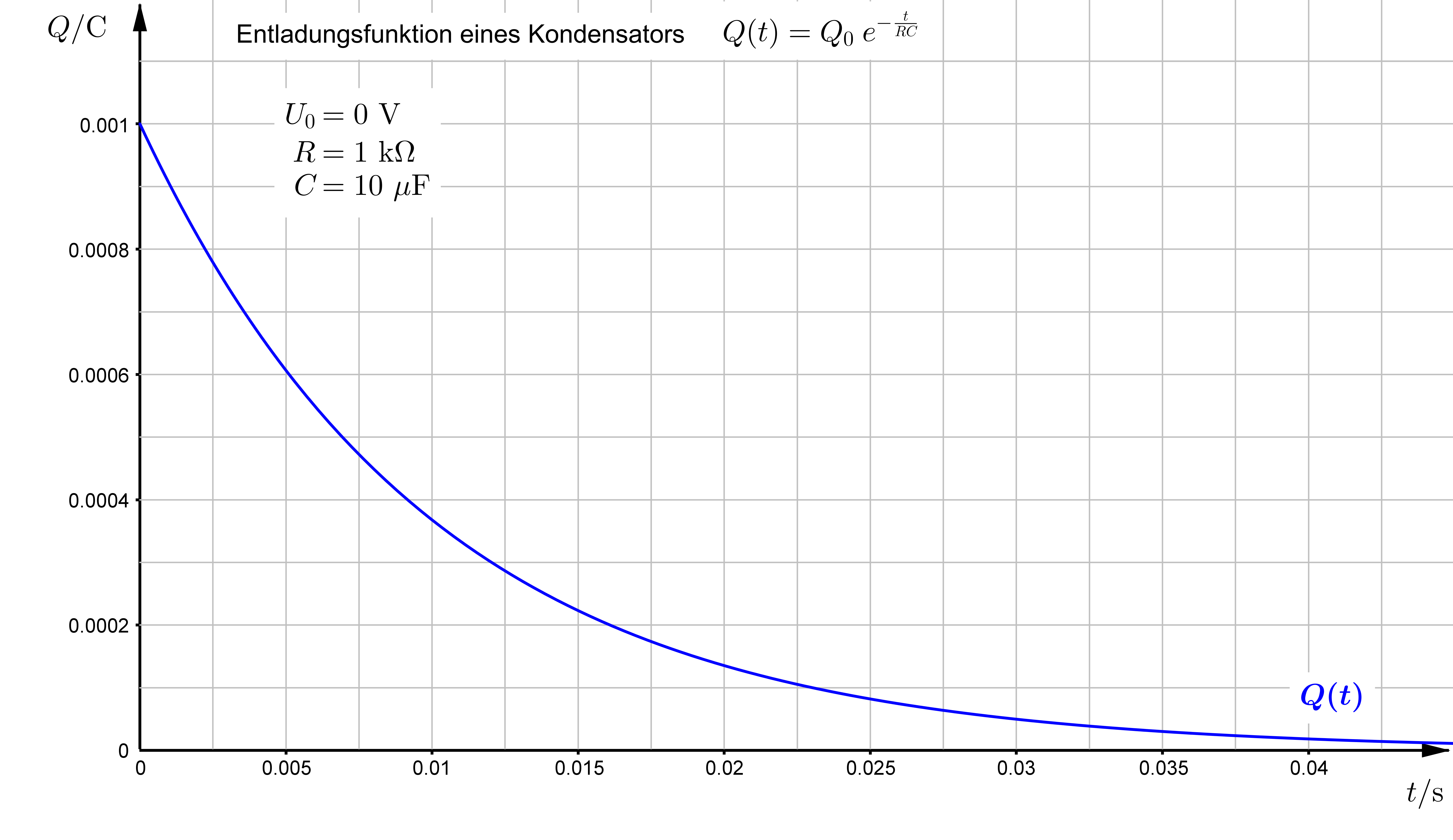
© mondbrand MMXIX