Lösung zu Aufgabe 3 (Extremwertaufgaben)
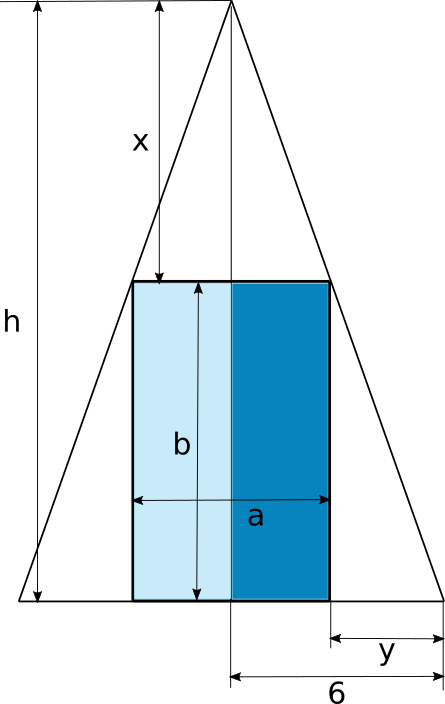Für dieses Problem lohnt sich eine Skizze.
Für die Höhe des gleichschenkligen Dreiecks gilt der Satz des Pythagoras:
$$
a^2 + b^2 = c^2 \\
6^2 + h^2 = 18^2 \\
h = \sqrt{18^2 - 6^2} \\
h = 16,97
$$
Zunächst wird nur die eine Hälfte des Rechtecks bestimmt. Für die Fläche dieses Rechtecks gilt: $A_r = \left( h - x \right) \cdot \left( 6 - y \right)$.
Der gesamte Flächeninhalt ist dann
$$
A = 2 \cdot \left( h - x \right) \cdot \left( 6 - y \right)
$$
und soll maximal werden.
Die Zielfunktion ist
allerdings abhängig von den zwei Variablen $x$ und $y$. Eine mögliche Nebenbedingung ergibt sich aus der Ähnlichkeit von Dreiecken. Es gilt
nämlich: $\frac{6}{h} = \frac{y}{h-x}$. Umgeformt nach $y$ erhält man:
$$
y = \left( h-x \right) \cdot \frac{6}{h}
$$
Damit wird die Zielfunktion zu
\begin{align}
A &= 2 \cdot \left( h - x \right) \cdot \left( 6 - \left( h-x \right) \cdot \frac{6}{h} \right) \\ \\
A &= 2 \cdot \left( h - x \right) \cdot \left( 6 - 6 + \frac{6x}{h} \right) \\ \\
A &= 2 \cdot \left( h - x \right) \cdot \frac{6x}{h} \\ \\
A &= 2 \cdot \left( 6x - \frac{6x^2}{h} \right) \\ \\
A &= 12x - \frac{12x^2}{h} \\ \\
A' &= 12 - \frac{24x}{h} \qquad \qquad A' = 0 \\
12 - \frac{24x}{h} &= 0 \\
x &= \frac{h}{2} \\ \\
A'' &= -\frac{24}{h} < 0 \qquad \rightarrow \qquad x \text{ ist ein Maximum}
\end{align}
Damit entspricht die Höhe des Rechtecks der halben Höhe des Dreiecks, also $b = h-x = 8,485 \text{ cm}$. Mit bekanntem $x$ kann $y$ bestimmt
werden: $y = 3$. Die Breite des Rechtecks entspricht also auch die Hälfte der Beite des Dreiecks: $a = 12 - 2y = 6 \text{ cm}$.