Extremwertaufgaben

Das Problem

Das Problem bei den Extremwertaufgaben besteht darin, eine Größe extrem groß (maximal) bzw. extrem klein (minimal) zu bekommen. Die Komplexität dieser Aufgaben erklärt sich zum kleineren Teil aus der Kenntnis oder Nichtkenntnis der elementaren Zusammenhänge von Funktion, Ableitung und Nullstellen bzw. Vorzeichen von Ableitungen. Die größeren Schwierigkeiten bereiten die Aufgabenstellungen selbst. Extremwertaufgaben sind meistens Textaufgaben, die zuerst verstanden werden müssen. Dabei müssen in den allermeisten Fällen geometrische Verhältnisse betrachtet werden. Die Anwendung der Methoden der Differentialrechnung ist erst möglich, wenn die Aufgabe in ein geeignetes mathematisches Modell übersetzt worden ist.

Die Lösung

Extremwertaufgaben, die als Textaufgaben formuliert sind, werden in folgenden Schritten gelöst:

Stelle die Aufgabensituation, wenn möglich, in einer Skizze dar.

Schreibe auf, was gegeben und was gesucht ist. Gib den Ausgangsgrößen und Unbekannten passende Namen ($a$, $x$, $q$, $A$, $F$, $V$ usw).

Erkenne die Zielfunktion und formuliere sie als mathematische Funktion in Abhängigkeit von den Ausgangsgrößen und Unbekannten.

Erkenne die Nebenbedingung. Die Wahl der zu bestimmenden Größen muss durch die Aufgabe in irgendeiner (evtl. versteckten) Weise eingeschränkt sein. Formuliere die Nebenbedingung als mathematischen Ausdruck.

Hat man die Zielfunktion, die meist aus mehreren voneinander abhängigen Variablen besteht und die Nebenbedingungen, die die voneinander abhängigen Variablen zueinander in Beziehung setzt, formuliert, dann kommt die Differentialrechnung zur Anwendung: Drücke mit Hilfe der Nebenbedingung alle Variablen durch eine fest gewählte Variable aus.

Setze die Nebenbedingungen in die Zielfunktion so ein, dass eine äquivalente Zielfunktion für den zu optimierenden Wert in Abhängigkeit von nur einer Variablen entsteht.

Bestimme Maximum oder Minimum der Zielfunktion durch Nullsetzen der ersten Ableitung und Überprüfung des Vorzeichens der zweiten Ableitung. Ein lokales Maximum liegt vor, wenn die zweite Ableitung an der Nullstelle kleiner als Null ist. Entsprechend liegt ein lokales Minimum vor, wenn die zweite Ableitung an der Nullstelle größer als Null ist. Man beachte dabei den möglicherweise durch die Aufgabenstellung implizit eingeschränkten Definitionsbereich (z.B. ist manchmal eine negative Länge sinnlos) und die Ränder des Definitionsbereichs. Es sind Situationen denkbar, in denen zwar im Definitionsbereich ein lokales Extremum vorliegt, aber die Zielfunktion ihr absolutes Extremum am Rand des Definitionsbereichs annimmt. Diese Werte findet man in der Regel nicht durch Differenzieren. Die Ränder müssen gesondert geprüft werden: durch Einsetzen der Randwerte in die Zielfunktion und Vergleich des Funktionswertes mit dem lokalen Extremum. Bei Extremwertaufgaben gibt es immer eine Zielfunktion, deren Wert maximiert/minimiert werden soll und eine Nebenbedingung, die die Wahl der Variablen in der Zielfunktion beschränkt.

Aufgabe 1

Gesucht ist eine positive Zahl, für welche die Summe aus deren Quadrat und deren Kehrwert minimal wird.

zur Lösung

Aufgabe 2

Aus einem 120cm langen Draht soll das Kantenmodell eines Quaders hergestellt werden, bei dem eine Kante dreimal so lang wie eine andere und der Rauminhalt möglichst groß ist. Bestimmen Sie das maximale Volumen.

zur Lösung

Aufgabe 3

Einem gleichschenkligen Dreieck mit der Grundseite $c = 12 \text{ cm}$ und der Schenkellänge $a = b = 18 \text{ cm}$ ist ein Rechteck mit maximalem Flächeninhalt einzubeschreiben. Berechnen Sie die Seitenlängen des Rechtecks.

zur Lösung

Aufgabe 4

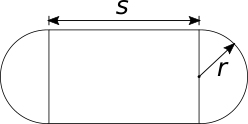Welche Maße muss ein Fussballplatz haben, damit ihn eine 400 m-Bahn umschließt und er möglichst groß ist?

zur Lösung

Aufgabe 5

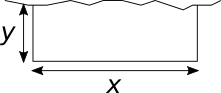Einem Schäfer stehen Zaunelemente der Gesamtlänge $s$ zur Verfügung. Damit will er eine rechteckige Einzäunung bauen, wobei eine Seite von einer Felswand gebildet wird. Welche Maße muss er dem Rechteck geben, damit die Fläche möglichst groß wird?

zur Lösung

Aufgabe 6

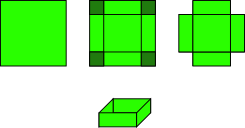Wie müssen die quadratischen Eckstücke eines gegebenen Quadrats bemessen sein, damit eine Schachtel mit größtem Volumen entsteht?

zur Lösung