Lösung zu Aufgabe 5 (Extremwertaufgaben)
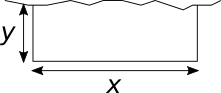Die Zielfunktion ist
$$
A = x \cdot y
$$
Mit der Nebenbedingung wird eine Beziehung zwischen den beiden Unbekannten gesucht. Hier ist die Gesamtlänge der Umzäunung $s$ bekannt.
Es gilt: $s = x + 2 \cdot y$ oder nach $y$ umgeformt:
$$
y = \frac{s}{2} - \frac{x}{2}
$$
Dieser Ausdruck wird in die Zielfunktion eingesetzt.
\begin{align}
A &= x \cdot \left( \frac{s}{2} - \frac{x}{2} \right) \\ \\
A &= - \frac 12 x^2 + \frac s2 x
\end{align}
Die Ableitungsfunktion $A'$ wird gleich Null gesetzt, um den Maximalwert für $A$ zu bekommen.
\begin{align}
A' &= - x + \frac s2 \qquad ; \qquad A' = 0 \\ \\
- x + \frac s2 &= 0 \\ \\
x &= \frac s2
\end{align}
Für die zweite Ableitung gilt: $A'' = -1 < 0$. Also ist der Extrempunkt ein Maximum.
Es folgt für $y$:
\begin{align}
y &= \frac{s}{2} - \frac{\frac s2}{2} \\ \\
y &= \frac{s}{2} - \frac{s}{4} \\ \\
y &= \frac s4
\end{align}
Damit muss die Länge $x = \frac s2$ und die Länge $y = \frac s4$ sein.