Lösung zu Aufgabe 4 (Extremwertaufgaben)
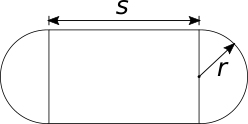Der gesamte Umfang der Anlage in der Skizze soll 400 m betragen. Damit folgt die erste Gleichung:
$$
400 \; \text{m} = 2 \cdot s + 2 \pi \cdot r
$$
Erläuterung: Der Weg besteht aus den beiden Geraden $s$ und zwei Halbkreisen, also einem Vollkreis mit dem Umfang $2 \pi r$.
Die Zielfunktion betrifft aber die Fläche, die maximal sein soll. Die Fläche des Spielfelds ist nach der Skizze
$$
A = s \cdot 2 \cdot r
$$
Die erste Gleichung wird nun nach einer der unbekannten Größen umgestellt, z.B. nach $r$:
\begin{align}
400 \; \text{m} &= 2 \cdot s + 2 \pi \cdot r \\ \\
400 \; \text{m} - 2 \cdot s &= 2 \pi \cdot r \\ \\
\frac{400 \; \text{m} - 2 \cdot s}{2 \pi} &= r
\end{align}
Dieses eingesetzt in die Zielfunktion führt zu:
\begin{align}
A &= s \cdot 2 \cdot \frac{400 \; \text{m} - 2 \cdot s}{2 \pi} \\ \\
A &= \frac{s (400 \; \text{m} - 2 \cdot s)}{\pi} \\ \\
A &= \frac{s \cdot 400 \; \text{m}}{\pi} - \frac{2 \cdot s^2}{\pi}
\end{align}
Oder etwas anders sortiert:
$$
A = - \frac{2}{\pi} \cdot s^2 + \frac{400 \; \text{m}}{\pi} \cdot s
$$
Den Maximalwert der Fläche bekommt man, indem die erste Ableitung der Flächenfunktion gleich Null gesetzt wird. Also
\begin{align}
A' &= - \frac{4}{\pi} \cdot s + \frac{400 \; \text{m}}{\pi} \qquad ; \qquad A' = 0 \\ \\
- \frac{4}{\pi} \cdot s + \frac{400 \; \text{m}}{\pi} &= 0 \\ \\
s &= \frac{400 \; \text{m}}{4} \\ \\
s &= 100 \; \text{m}
\end{align}
Mit der zweiten Ableitung $A'' = - \frac{4}{\pi} < 0$ folgt, dass der berechnete Wert für $s$ zu einem Maximum gehört.
Mit der Gleichung für $r$ folgt
\begin{align}
r &= \frac{400 \; \text{m} - 2 \cdot s}{2 \pi} \\ \\
r &= \frac{400 \; \text{m} - 2 \cdot 100 \; \text{m}}{2 \pi} \\ \\
r &= 31,83 \; \text{m}
\end{align}
Damit ist das Spielfeld $2 \cdot 31,83 \; \text{m} = 63,66 \; \text{m}$ breit.
Das Spielfeld hat also die Maße $100 \; \text{m} \times 63,66 \; \text{m}$.