Lösung zu Aufgabe 1 (ganzrationale Funktionen im Sachzusammenhang)

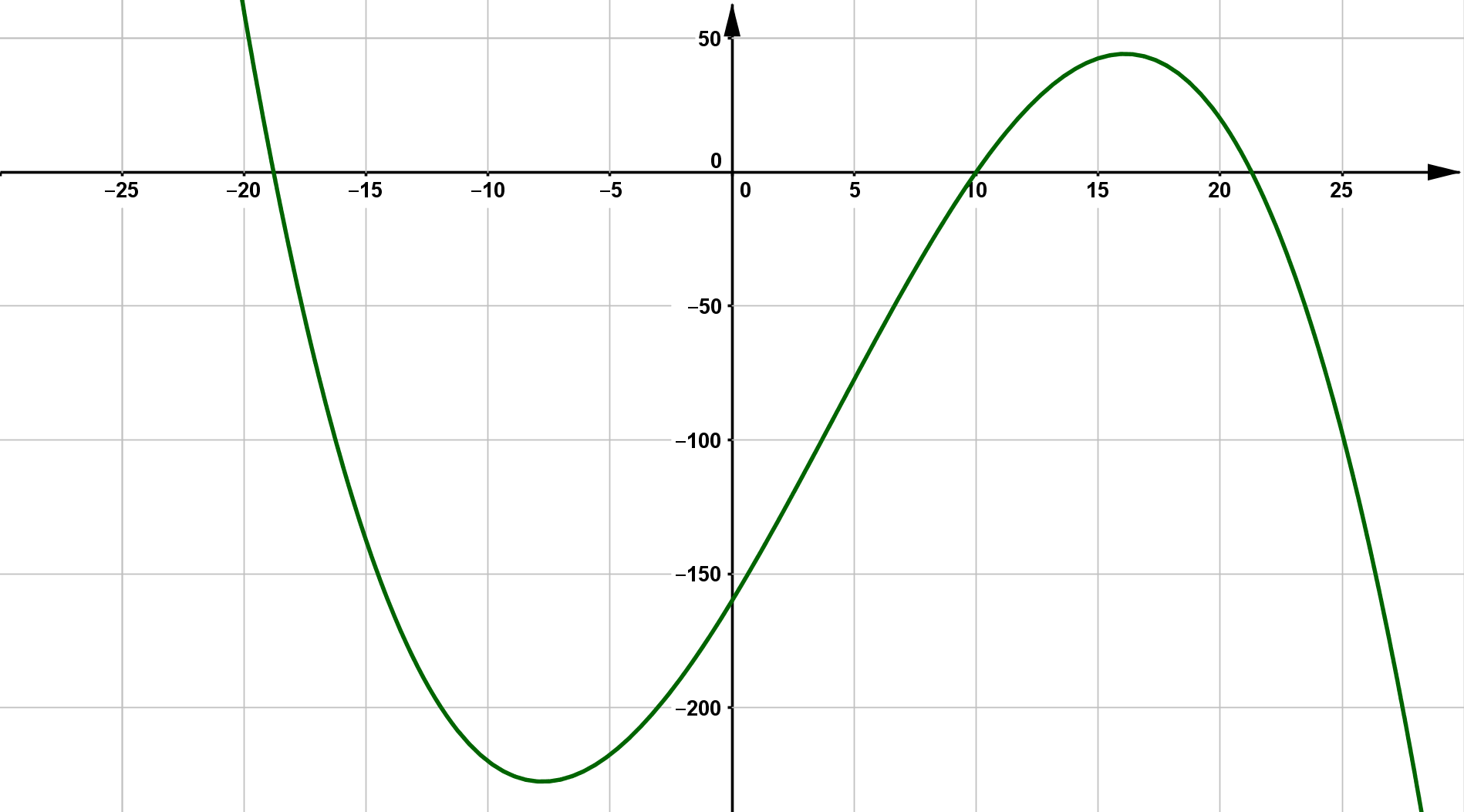
Ein Schnellrestaurant öffnet von 10:00 Uhr bis 21:30 Uhr. Es werden die Besucherzahlen über einen längeren Zeitraum notiert. Aus den Daten ergibt sich ein Funktionsterm $f$, der die Besucherzahlen in Abhängigkeit von der Tageszeit beschreibt. Die zugehörige Funktionsgleichung lautet: $$ f(x) = -0,04 x^3 + 0,5 x^2 + 15 x - 160 $$ Der zu der Gleichung gehörende Graph ist in der Abbildung zu sehen.

Definieren Sie den für den Sachzusammenhang notwendigen Definitionsbereich für $f$.
Geben Sie die Anzahl der Besucher zwei Stunden nach Öffnung an.
Interpretieren Sie die Bedeutung der Nullstellen.

Bestimmen Sie den Zeitpunkt, an dem der letzte Besucher das Restaurant verlässt.
Zu welchem Zeitpunkt ist die Anzahl der Besucher am größten und wieviele Besucher sind es?

Die Funktion beschreibt eine Anzahl von Menschen in Abhängigkeit von der Tageszeit. Zunächst gibt es keine negative Anzahl von Besuchern. Damit liegt der Wertebereich der Funktion im positiven $y$-Bereich. Die Tageszeit beginnt um 0:00 Uhr und endet um 24:00 Uhr. Damit ist der Definitionsbereich der Funktion $D = \{0 \le x \le 24 \}$, d.h. alle $x$-Werte zwischen 0 und 24. Der relevante Graph sieht dann so aus:

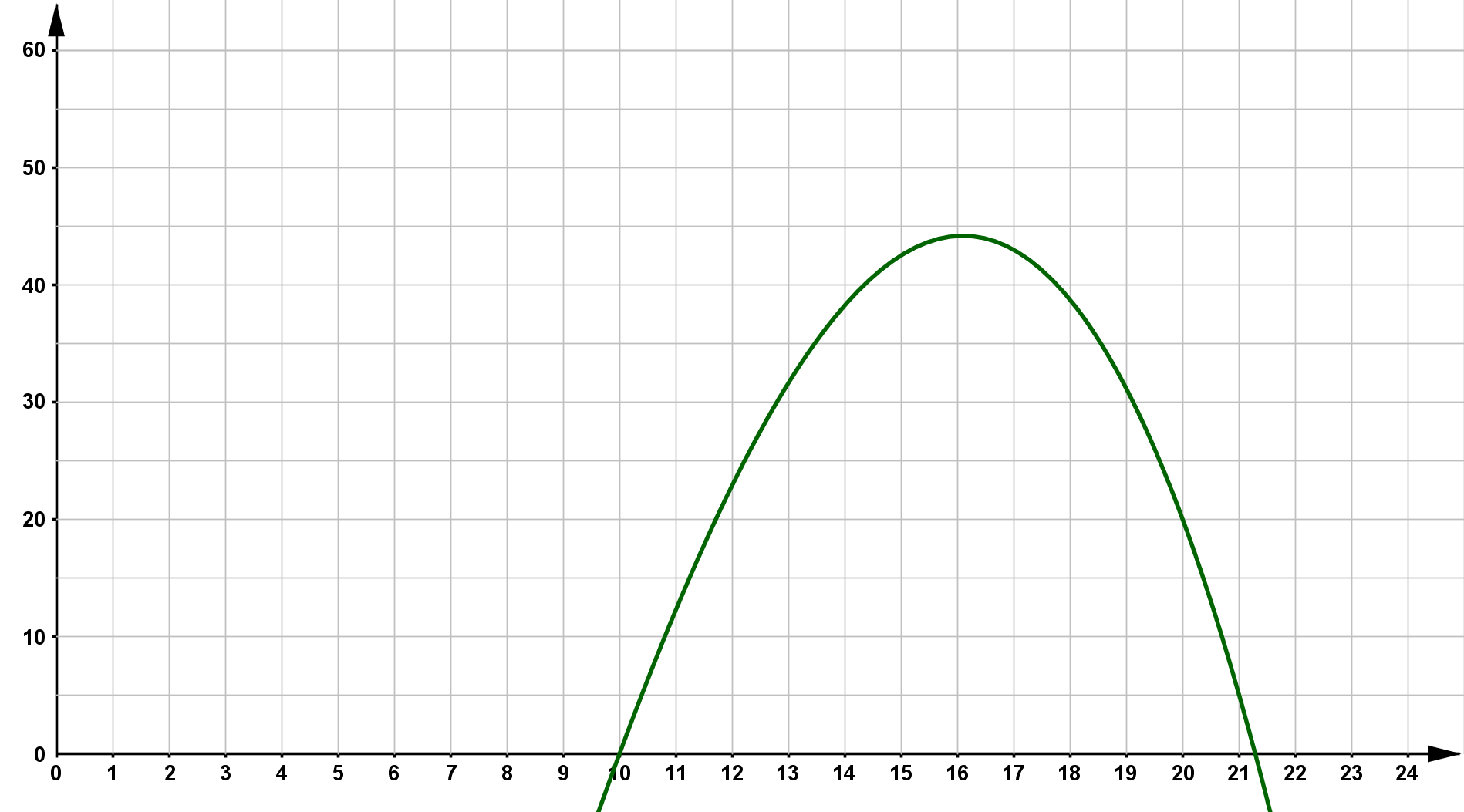
Zwei Stunden nach Öffnung heißt 12:00 Uhr. Gesucht ist also $f(12)$. $$ f(12) = -0,04 \cdot 12^3 + 0,5 \cdot 12^2 + 15 \cdot 12 -160 = 22,88 $$ Damit sind um 12:00 Uhr ca. 23 Besucher im Restaurant.

Die Nullstellen geben an, wann der erste Besucher das Restaurant betritt (erste Ns. im Definitionsbereich) und wann der letzte Besucher das Restaurant verlässt (zweite Ns. im Definitionsbereich).

Gesucht ist also die letzte Nullstelle. Da der Funktionsterm eine allgemeine Funktion dritten Grades ist, lassen sich die Nullstellen nicht ohne weiteres bestimmen. Mit der Information $x_{N1} = 10$ kann aber der Funktionsterm durch Polynomdivision vereinfacht werden. Die Nullstelle bildet den Linearfaktor $x - 10$. Es folgt:

$-0,04x^3$	$+$	$0,5 x^2$	$+$	$16 x$	$-$	$160$	$ : (x-10) = -0,04x^2 +0,1 x + 16$
$- ( -0,04x^3$	$+$	$0,4 x^2)$
		$0,1 x^2$	$+$	$15 x$	$-$	$160$
	$-$	$(0,1 x^2$	$-$	$ 1 x)$
				$16 x$	$-$	$160$
			$-$	$(16 x$	$-$	$160)$
						$0$

Die Untersuchung der Nullstellen kann also mit der quadratischen Gleichung durchgeführt werden. Es folgt: \begin{align} - 0,04 x^2 + 0,1 x + 16 &= 0 \\ x^2 - 2,5 x - 400 &= 0 \qquad \qquad \qquad p = - 2,5 \; ; \; q = - 400 \\ \\ x_{1,2} &= - \frac{- 2,5}{2} \pm \sqrt{\left(\frac{-2,5}{2}\right)^2 - (- 400)} \\ \\ x_1 = - 18,79 \quad &; \quad x_2 = 21,29 \end{align} Die Nullstelle im Definitionsbereich ist $x_{N2} = 21,29$.
Da 0,29 Stunden gleich 17,4 Minuten sind, folgt, dass der letzte Besucher das Restaurant um 21:17 Uhr verlässt.

Die größte Besucheranzahl ist das Maximum des Funktionsgraphen. Um das zu finden, werden die Ableitungen $f'(x)$ und $f''(x)$ benötigt: $$ f'(x) = - 0,12 x^2 + x + 15 \qquad \qquad f''(x) - 0,24 x + 1 $$ Die Bedingungen für Extremstellen lauten: $f'(x) = 0 \land f''(x) \gtrless 0$

Zunächst die notwendige Bedingung: \begin{align} - 0,12 x^2 + x + 15 &= 0 \\ x^2 - \frac{25}{3} x - 125 &= 0 \qquad \qquad \qquad p = - \frac{25}{3} \; ; \; q = - 125 \\ \\ x_{1,2} &= \frac{25}{6} \pm \sqrt{\left(\frac{25}{6}\right)^2+125} \\ \\ x_1 = -7,76 \quad &; \quad x_2 = 16,10 \\ \\ \\ f''(16,10) &= - 2,9 \lt 0 \; \rightarrow \; x_2 \text{ ist ein Maximum} \\ \\ \\ f(16,10) &= 44,17 \end{align} Um 16:06 Uhr sind mit ca. 44 Besuchern die meisten Gäste im Restaurant.

Zurück zu der Aufgabe