Ganzrationale Funktionen

Aufgaben im Sachzusammenhang

Zunächst als Vorbemerkung:
Für die Bearbeitung der folgenden Aufgaben ist es notwendig, dass der Begriff der Ableitung von ganzrationalen Funktionen bekannt ist. Die Potenzregel, die Faktorregel und die Konstantenregel, sowie die Summenregel sollten ohne Schwierigkeiten angewendet werden können.

Für viele Phänomene aus Natur und Technik werden Funktionen genutzt, um das Verhalten von bestimmten Größen zu beschreiben. Wichtiger noch: mit dem Begriff der Änderungsrate und damit der Ableitung wird die Veränderung bestimmter Größen beschrieben. Aus diesem Grund werden viele Aufgaben in einem Sachzusammenhang gestellt, da die Formulierungen und Aufgabenstellungen in der Realität nicht lauten: „Bestimmen Sie den Wendepunkt der Funktion".

Somit ist es erforderlich, den Aufgabentext genau und vollständig zu lesen, damit man erkennt, was für die Bearbeitung einer jeden Aufgabenstellung eigentlich notwendig ist. Denn die Werkzeuge, d.h. Ableitungen bilden, Nullstellen bestimmen, ..., sind natürlich dieselben, wie bei „Bestimmen Sie den Wendepunkt der Funktion".

Aufgabe 1

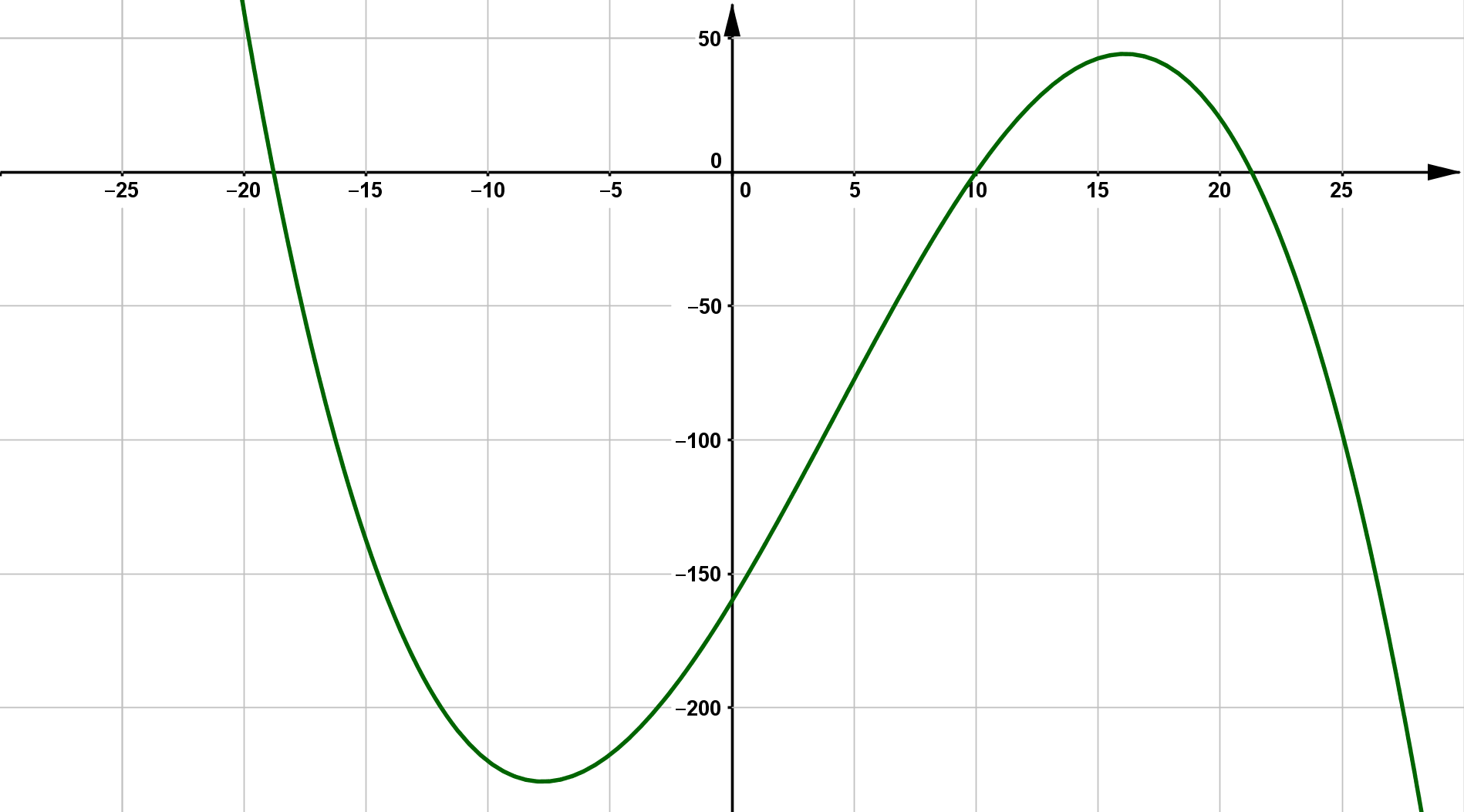
Ein Schnellrestaurant öffnet von 10:00 Uhr bis 21:30 Uhr. Es werden die Besucherzahlen über einen längeren Zeitraum notiert. Aus den Daten ergibt sich ein Funktionsterm $f$, der die Besucherzahlen in Abhängigkeit von der Tageszeit beschreibt. Die zugehörige Funktionsgleichung lautet: $$ f(x) = -0,04 x^3 + 0,5 x^2 + 15 x - 160 $$ Der zu der Gleichung gehörende Graph ist in der Abbildung zu sehen.

Definieren Sie den für den Sachzusammenhang notwendigen Definitionsbereich für $f$.
Geben Sie die Anzahl der Besucher zwei Stunden nach Öffnung an.
Interpretieren Sie die Bedeutung der Nullstellen.

Bestimmen Sie den Zeitpunkt, an dem der letzte Besucher das Restaurant verlässt.
Zu welchem Zeitpunkt ist die Anzahl der Besucher am größten und wieviele Besucher sind es?

zur Lösung

Aufgabe 2

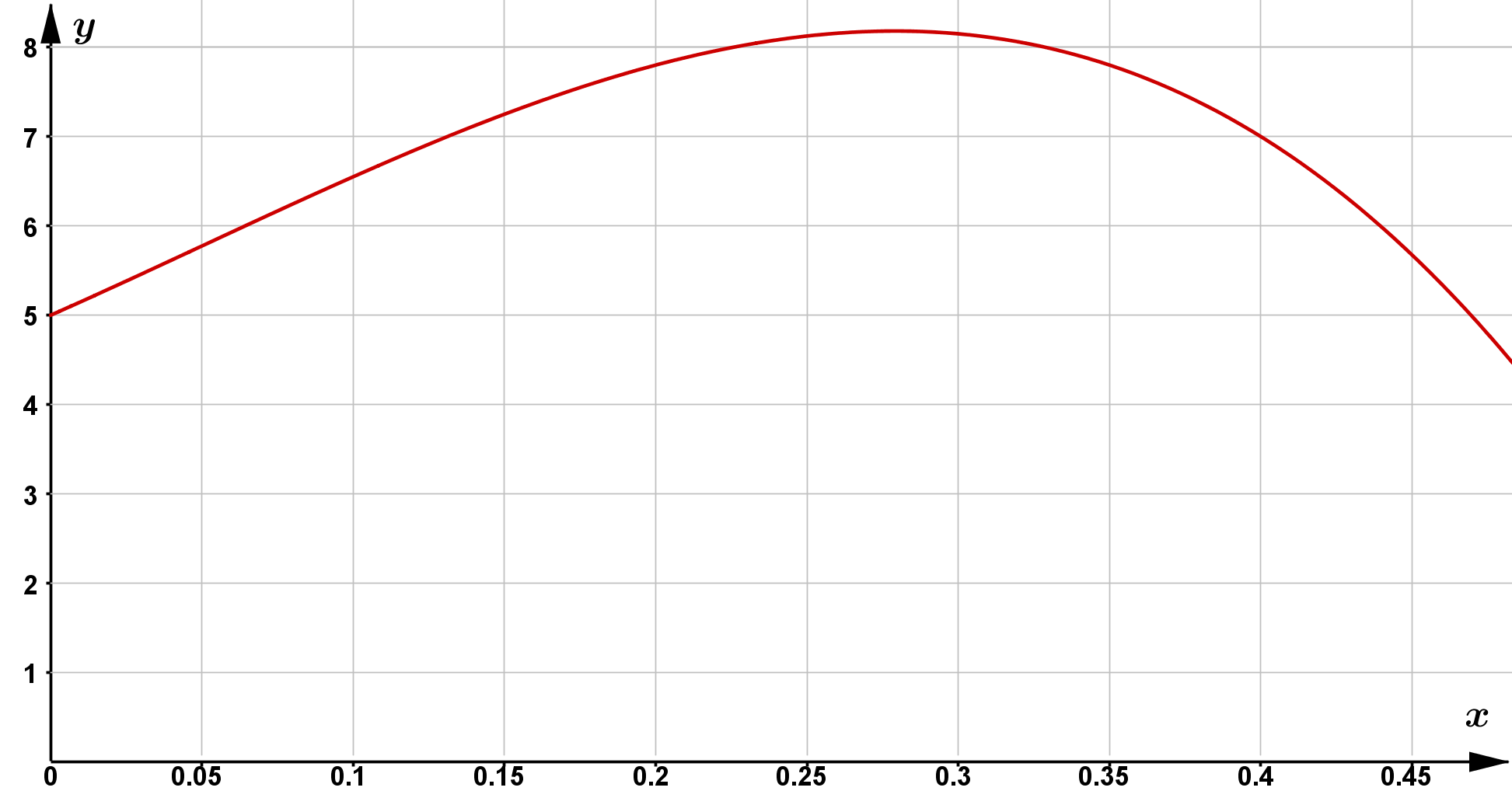
Um den Ertrag einer angebauten Weizensorte zu steigern, wird dem Weizen Dünger hinzugefügt. Wird zuviel gedüngt, nimmt der Ertrag wieder ab. Die Abbildung zeigt den funktionalen Zusammenhang zwischen Ertrag und Düngermenge. Dem Graphen liegt die folgende Funktionsgleichung zugrunde: $$ f(x) = -100 x^3 + 15 x^2 + 15 x + 5 $$ Dabei ist $x$ die Düngermenge in Tonnen pro Hektar und $f(x)$ der Ertrag in Tonnen pro Hektar.
Der Graph wird bereits im für den Sachzusammenhang relevanten Bereich angezeigt.

Geben Sie den Ertrag bei einer Düngermenge von 0,1 t/ha an.
Berechnen Sie die Düngermenge so, dass der Ertrag maximal wird.
Berechnen Sie die Wendestelle der Funktion, die Steigung des Graphen an dieser Stelle und interpretieren Sie die Ergebnisse im Sachzusammenhang.

Bestimmen Sie eine Gleichung, die den Gewinn pro Hektar in Abhängigkeit von der Düngermenge beschreibt. Berechnen Sie den maximalen Gewinn.

zur Lösung

Aufgabe 3

Die durch ein elektrisches Bauteil fließende Ladung $Q$ (in der Einheit Coulomb; [Q} = 1 C) wird durch die Funktion $Q$ mit der Gleichung $$ Q(t) = -0,1 t^3 + 1,1 t^2 - 3 t + 3 $$ beschrieben. Die momentane Änderungsrate $Q'(t)$ entspricht der elektrischen Stromstärke $I(t)$. Die Zeit $t$ wird in Sekunden angegeben.

Bestimmen sie die fließende Ladungsmenge nach einer Sekunde.
Welche Ladungsmenge fließt nach 5 s? Wann fließt keine Ladung?
Berechnen Sie die Stromstärke zum Zeitpunkt $t = 0$.
Welche Stromstärke liegt vor, wenn keine Ladung mehr fließt?
Bestimmen Sie die maximale Stromstärke. Wann liegt sie vor?
In welchem Zeitintervall ist die Stromstärke positiv?

zur Lösung