Lösung zu Aufgabe 2 (ganzrationale Funktionen im Sachzusammenhang)
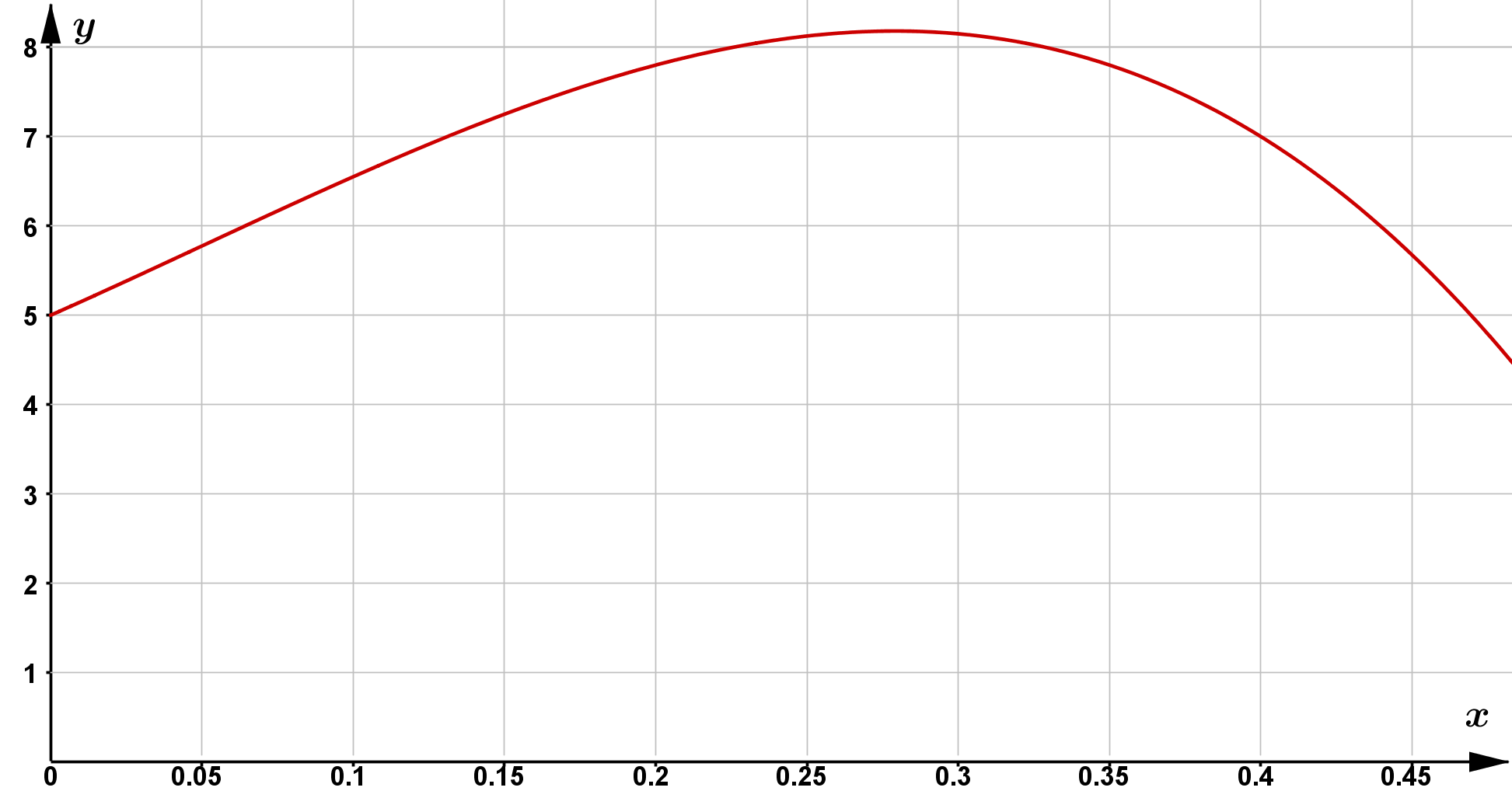
Um den Ertrag einer angebauten Weizensorte zu steigern, wird dem Weizen Dünger hinzugefügt. Wird zuviel gedüngt, nimmt der Ertrag wieder ab. Die Abbildung zeigt den funktionalen Zusammenhang zwischen Ertrag und Düngermenge. Dem Graphen liegt die folgende Funktionsgleichung zugrunde: $$ f(x) = -100 x^3 + 15 x^2 + 15 x + 5 $$ Dabei ist $x$ die Düngermenge in Tonnen pro Hektar und $f(x)$ der Ertrag in Tonnen pro Hektar.
Der Graph wird bereits im für den Sachzusammenhang relevanten Bereich angezeigt.
- Geben Sie den Ertrag bei einer Düngermenge von 0,1 t/ha an.
- Berechnen Sie die Düngermenge so, dass der Ertrag maximal wird.
- Berechnen Sie die Wendestelle der Funktion, die Steigung des Graphen an dieser Stelle und interpretieren Sie die Ergebnisse im Sachzusammenhang.
- Bestimmen Sie eine Gleichung, die den Gewinn pro Hektar in Abhängigkeit von der Düngermenge beschreibt. Berechnen Sie den maximalen Gewinn.
Angenommen, der Landwirt erzielt pro Tonne Weizen einen Gewinn von 150 € und der eingesetzte Dünger kostet ihn 300 € pro Tonne.
Gesucht ist zunächst der Ertrag für eine bestimmte Düngermenge. Da die Düngermenge auf der $x$-Achse aufgetragen wird, ist $f(x)$ gesucht, hier:
$$
f(0,1) = -100 \cdot 0,1^3 + 15 \cdot 0,1^2 + 15 \cdot 0,1 + 5 \\
f(0,1) = 6,55
$$
$f(x)$ bezeichnet den Ertrag in Tonnen pro Hektar. Das Ergebnis lautet somit:
Der Ertrag liegt bei 6,55 t/ha bei einer Düngermenge von 0,1 t/ha.
Maximaler Ertrag bedeutet, dass das Maximum des Graphen gesucht ist. Die dafür benötigten Ableitungsfunktionen lauten:
$$
f'(x) = -300 x^2 + 30 x + 15 \\
f''(x) = -600 x + 30
$$
Die Bedingungen für das Maximum lauten: $f'(x) = 0 \land f''(x) < 0$
\begin{align}
-300 x^2 + 30 x + 15 &= 0 \\
x^2 - 0,1 x - 0,05 &= 0 \qquad \qquad \qquad p = - 0,1 \; ; \; q = - 0,05 \\ \\
x_{1,2} &= - \frac{- 0,1}{2} \pm \sqrt{\left(\frac{-0,1}{2}\right)^2 + 0,05} \\ \\
x_1 = -0,18 \quad &; \quad x_2 = 0,28 \\ \\ \\
f''(-0,18) = 138 > 0 \quad &; \quad f''(0,28) = -138 < 0 \; \rightarrow \; x_2 \text{ ist ein Maximum} \\ \\ \\
f(0,28) &= 8,18
\end{align}
Da nur die Düngermenge gefragt ist (also der $x$-Wert), lautet die Antwort:
Der maximale Ertrag wird bei einer Düngermenge von 0,28 t/ha erzielt.
Für die Wendestelle gilt:
$$
f''(x) = 0 \land f'''(x) \neq 0
$$
Also folgt:
\begin{align}
-600 x + 30 &= 0 \\ \\
x &= 0,05
\end{align}
Die dritte Ableitung lautet: $f'''(x) = -600$. Sie ist für alle $x$-Werte ungleich Null.
Die Wendestelle ist somit: $x = 0,05$.
Die Steigung an dieser Stelle ist $f'(0,05) = 15,75$.
Im Sachzusammenhang bedeuten die Ergebnisse, dass der Ertrag sich bei einer Düngermenge von 0,05 t/ha am stärksten steigert, nämlich um
$\frac{15,75 t/ha}{t/ha}$.
Die bei der Bestimmung der Steigung herauskommenden Einheiten lassen sich wie folgt behandeln.
Zunächst beziehen sich beide Größen, also $f(x)$ und
$x$ auf eine Fläche von einen Hektar. Damit dürfen die beiden Einheiten miteinander verrechnet werden: Sie kürzen sich heraus. Bei der Mengenangabe
Tonnen bezieht sich $f(x)$ auf den Ertrag des Weizens und $x$ auf die Düngermenge, also auf unterschiedliche Sachen. Die Tonnen dürfen nicht
miteinander verrechnet werden. Es verbleibt eine Änderung von 15,75 t/t, also 15,75 Tonnen Weizen pro Tonne Dünger.