Eine ganzrationale Funktion ist die Summe von Potenzfunktionen mit natürlichen Exponenten. Eine andere Bezeichnung für die ganzrationale Funktion ist Polynomfunktion. Beschrieben wird eine ganzrationale Funktion allgemein durch: $$ f(x) = a_n \cdot x^n + a_{n-1} \cdot x^{n-1} + a_{n-2} \cdot x^{n-2} + \cdots + a_1 \cdot x^1 + a_0 $$ Für $n = 1$ ist die ganzrationale Funktion eine lineare Funktion mit der Steigung $m = a_1$ und dem Achsenabschnitt $b = a_0$. Für $n = 2$ erhält man die quadratische Funktion mit den Koeffizienten $a = a_2$, $b = a_1$ und $c = a_0$.
Der höchste Exponent der Potenzen zeigt den Grad der Funktion an. Eine quadratische Funktion ist damit eine ganzrationale Funktion zweiten Grades.
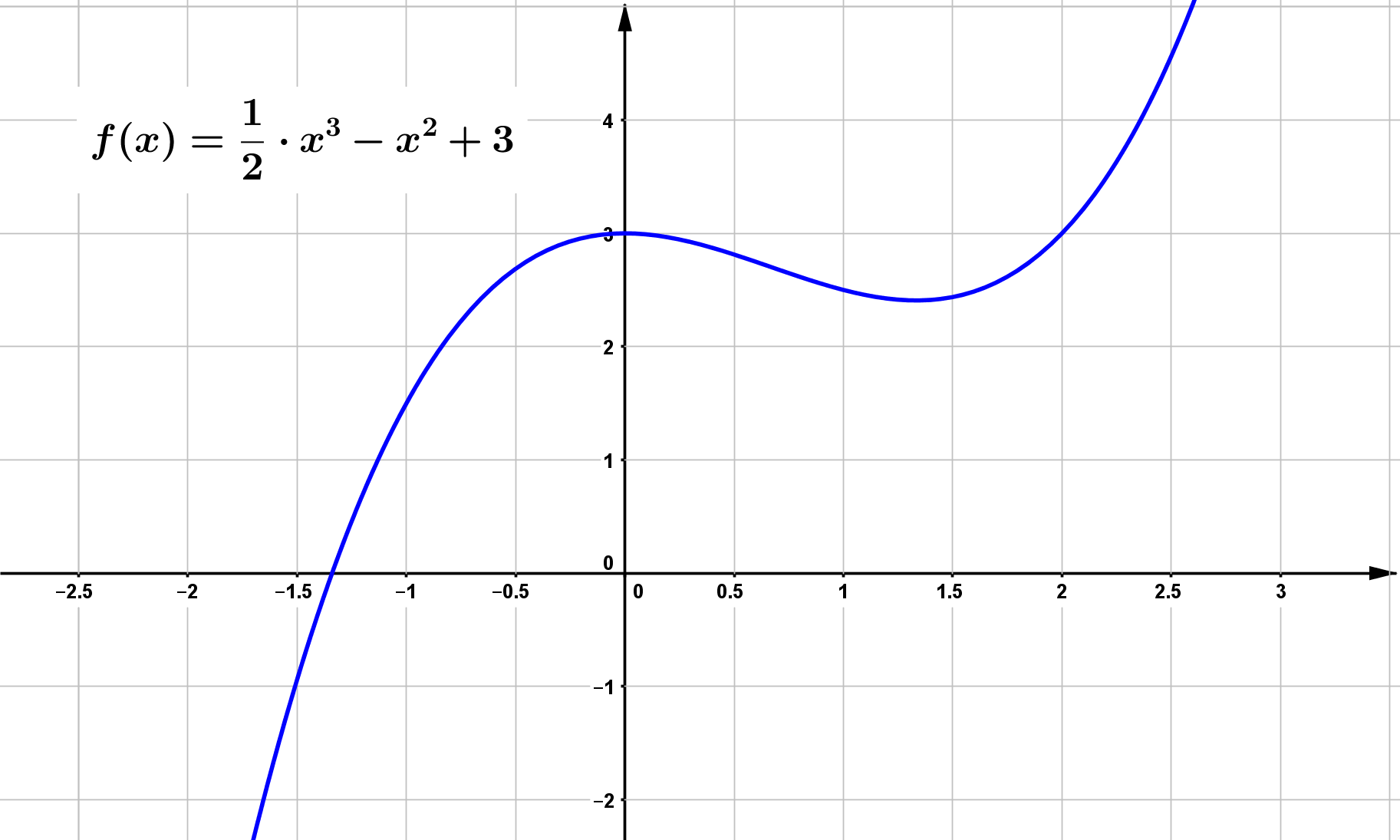
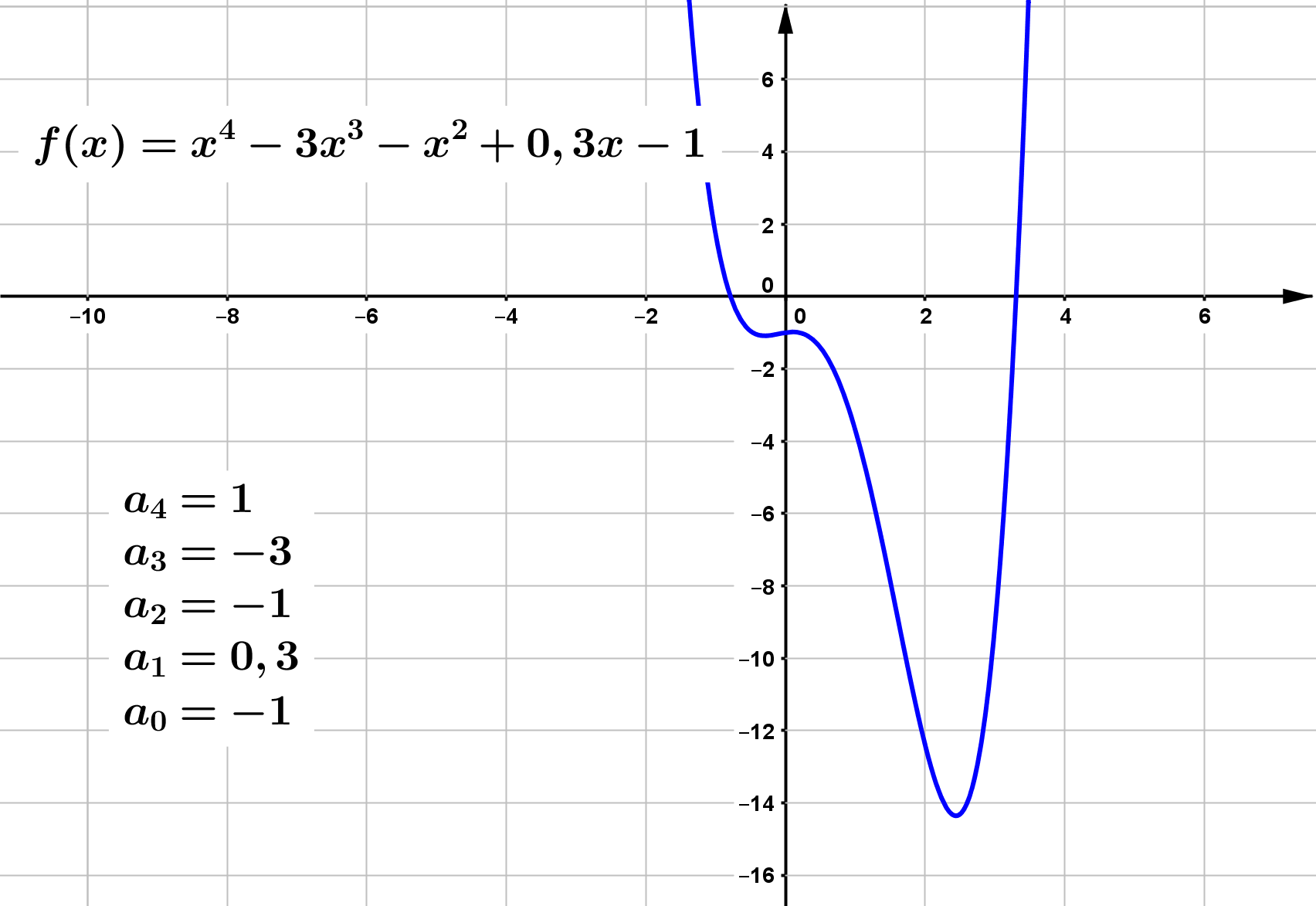
Eine wichtige Eigenschaft einer beliebigen Funktion ist der Globalverlauf. Unter dem Globalverlauf versteht man das Verhalten des Funktionsgraphen im
Unendlichen, d.h. wenn der $x$-Wert gegen $\pm \infty$ geht.
Für den Globalverlauf ist der Term mit dem höchsten Exponenten verantwortlich. Alle anderen Terme verlieren für größer werdende $x$-Werte gegenüber
dem Term mit dem höchsten Exponenten an Bedeutung.
Für die Untersuchung des Globalverlaufs muss zunächst zwischen geradzahligen und ungeradzahligen Exponenten unterschieden werden. Dann muss
noch unterschieden werden, ob der Koeffizient $a_n$ positiv oder negativ ist. Diese Unterscheidungen bilden die vier Möglichkeiten für den
Globalverlauf:
| $n$ geradzahlig | $n$ ungeradzahlig | |
| $a_n > 0$ | $f(x) \rightarrow \infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow \infty \text{ für } x \rightarrow \infty$ | $f(x) \rightarrow -\infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow \infty \text{ für } x \rightarrow \infty$ |
| $a_n < 0$ | $f(x) \rightarrow -\infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow -\infty \text{ für } x \rightarrow \infty$ | $f(x) \rightarrow \infty \text{ für } x \rightarrow -\infty \\ f(x) \rightarrow -\infty \text{ für } x \rightarrow \infty$ |
Die Symmetrie eines Funktionsgraphen bildet eine weitere wichtige Eigenschaft. Man kann viel über eine Funktion bzw. über ihren Verlauf herausfinden, wenn man ihre Symmetrieeigenschaften kennt.Hier sind alle Terme der Funktion wichtig.
Allgemein und für alle Funktionstypen kann die Symmetrie eines Graphen durch die folgenden Ansätze überprüft werden:
$$
f(x) = f(-x) \qquad \text{Achsensymmetrie} \\
f(x) = - f(-x) \qquad \text{Punktsymmetrie}
$$
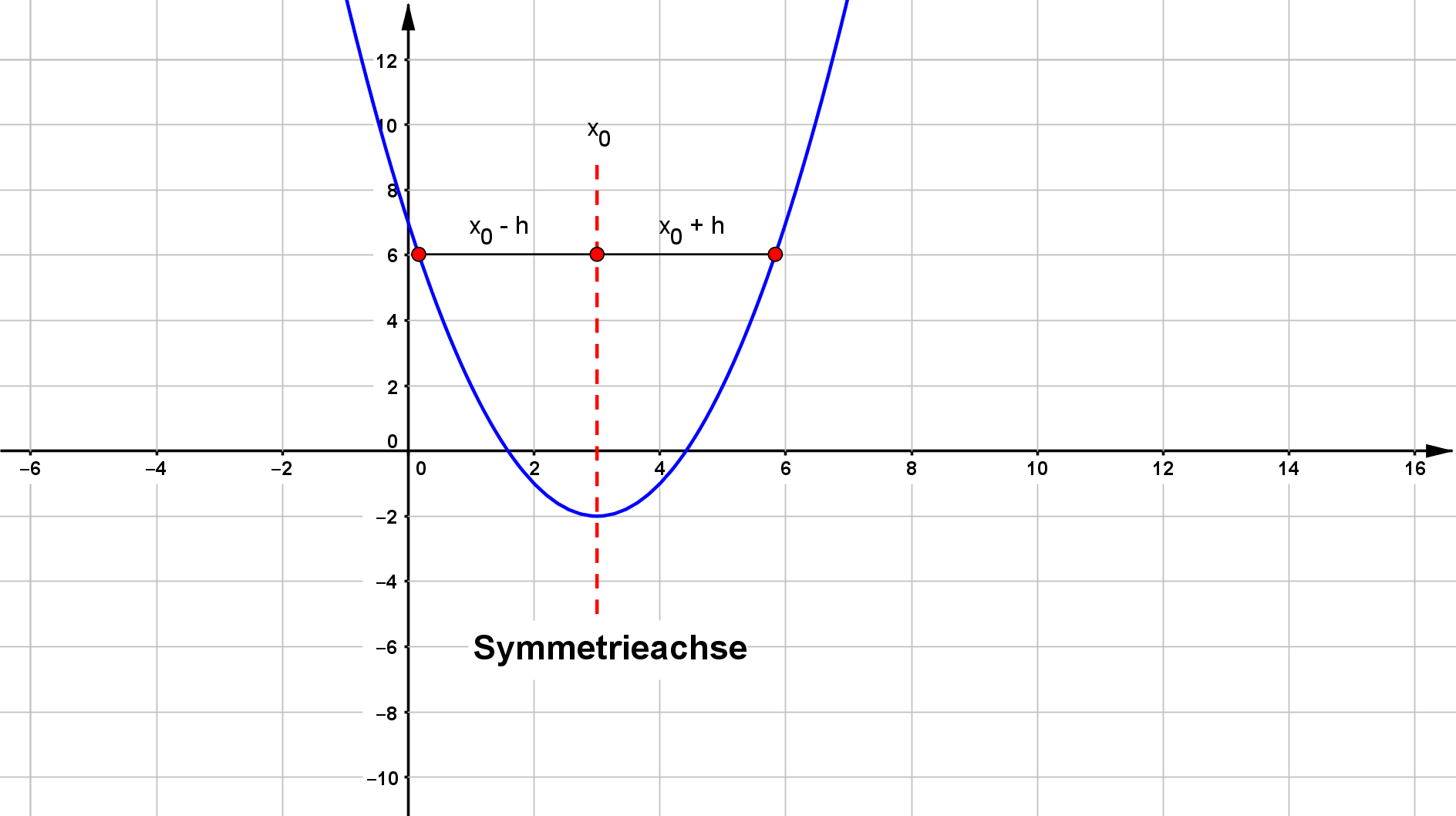Für die Überprüfung der Symmetrie bezüglich einer beliebigen Achse $x_0$ wird der folgende Ansatz verwendet:
$$
f(x_0 + h) = f(x_0 - h)
$$
Mit diesem Ansatz kann man entweder herausfinden, ob eine bestimmte Achse, z.B. $x_0 = 3$, eine Symmetrieachse ist. Dann entsteht aus dem Ansatz
eine wahre Aussage. Oder man findet heraus, an welcher Stelle $x_0$ die Symmetriebedingung erfüllt wird.
Für die Frage nach der Symmetrie bezüglich eines beliebigen Punktes im Koordinatensystem wird der folgende Ansatz verfolgt:
$$
f(x_0 + h) - f(x_0) = f(x_0) - f(x_0 - h)
$$
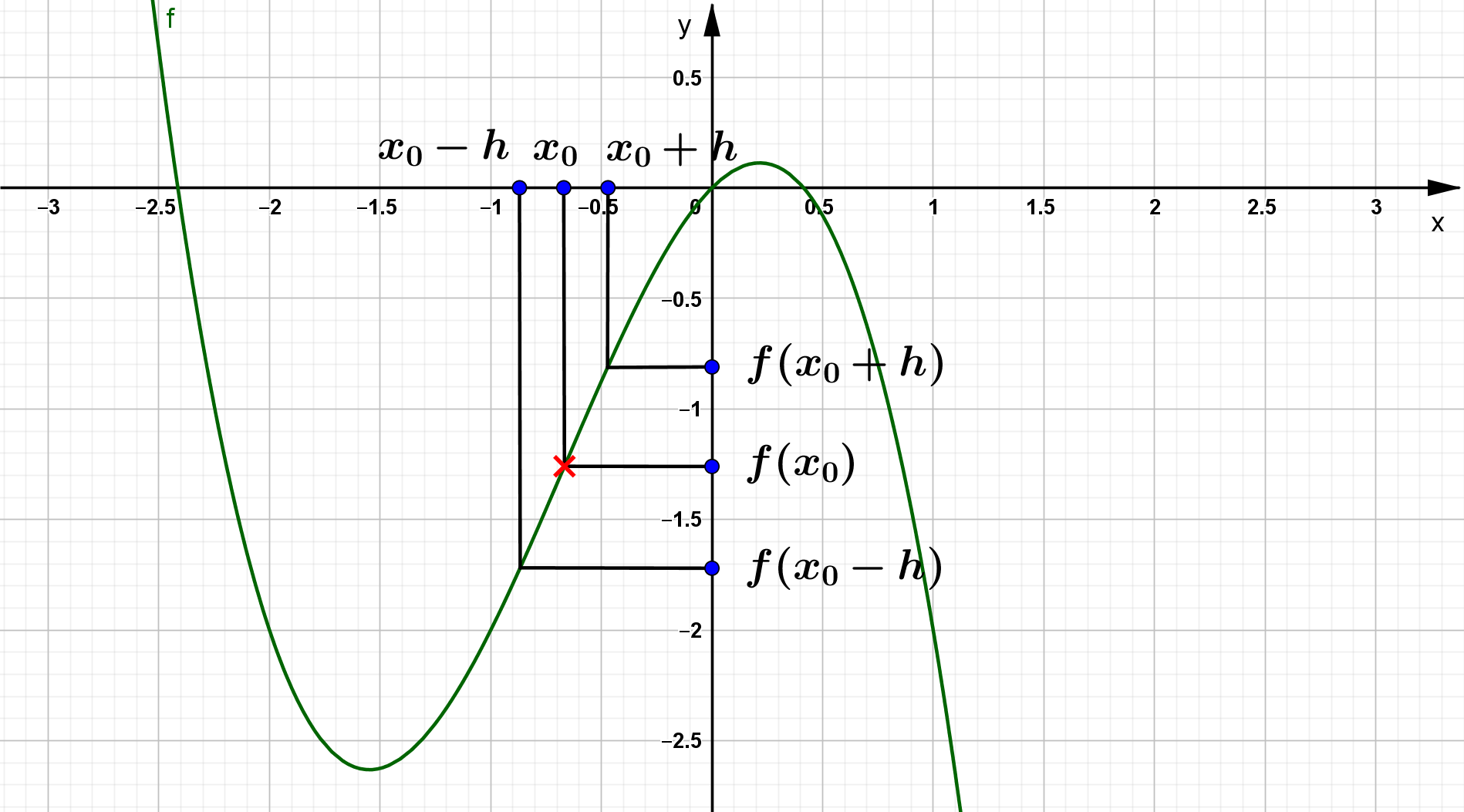
Auch hier kann wieder die Frage gestellt werden, ob ein bestimmter Punkt Symmetriepunkt ist (wahre Aussage) oder bei welchem Punkt die Symmetrie
gegeben ist (Gleichsetzen). Mit der in den Beispielen oben gegebenen Funktion $f(x) = - x^3 - 2x^2 + x$ soll das demonstriert werden:
Wegen der langen Zeilen wird zunächst der Term $f(x+h)$ bestimmt und vereinfacht, im Anschluss der Term $f(x-h)$.
\begin{align}
f(x+h) &= - (x+h)^3 - 2 (x+h)^2 + (x+h) \\
&= - (x^3 + 3x^2h + 3xh^2 + h^3) - 2 (x^2 + 2xh + h^2) + x + h \\
&= - x^3 - 3x^2h - 3 xh^2 - h^3 - 2x^2 - 4xh - 2h^2 + x + h \\
&= - x^3 - 2x^2 + x - 3x^2h - 4xh + h - 3xh^2 - 2h^2 - h^3
\end{align}
\begin{align}
&f(x+h) - f(x) \\
&= - x^3 - 2x^2 + x - 3x^2h - 4xh + h - 3xh^2 - 2h^2 - h^3 - (- x^3 - 2x^2 + x) \\
&= - x^3 - 2x^2 + x - 3x^2h - 4xh + h - 3xh^2 - 2h^2 - h^3 + x^3 + 2x^2 - x \\
&= - 3x^2h - 4xh + h - 3xh^2 - 2h^2 - h^3
\end{align}
\begin{align}
f(x-h) &= - (x-h)^3 - 2 (x-h)^2 + (x-h) \\
&= - ( x^3 - 3x^2h + 3xh^2 - h^3) - 2 (x^2 - 2xh + h^2) + x - h \\
&= - x^3 + 3x^2h - 3xh^2 + h^3 - 2x^2 + 4xh - 2h^2 + x - h \\
&= - x^3 - 2x^2 + x + 3x^2h + 4xh - h - 3xh^2 - 2h^2 + h^3
\end{align}
\begin{align}
&f(x) - f(x-h) \\
&= - x^3 - 2x^2 + x - ( - x^3 - 2x^2 + x + 3x^2h + 4xh - h - 3xh^2 - 2h^2 + h^3 ) \\
&= - x^3 - 2x^2 + x + x^3 + 2x^2 - x - 3x^2h- 4xh + h + 3xh^2 + 2h^2 - h^3 \\
&= - 3x^2h- 4xh + h + 3xh^2 + 2h^2 - h^3
\end{align}
© mondbrand MMXIX