

Gegeben sind die Eckpunkte eines Dreiecks $ABC$ mit $$A (0/-2), B (12/2), C(2/7).$$
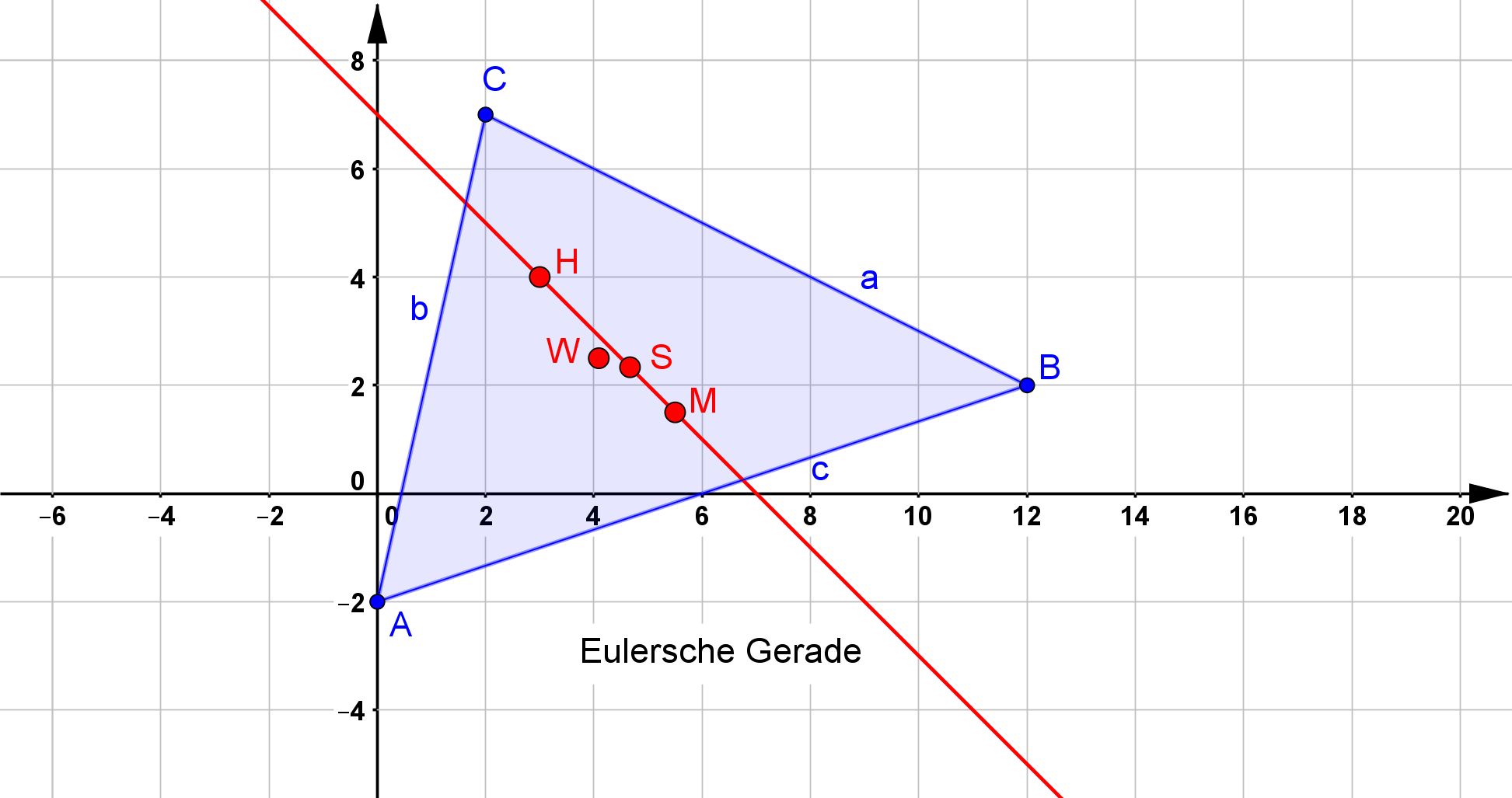
Zeigen Sie rechnerisch, dass der Umkreismittelpunkt $M$, der Flächenschwerpunkt $S$ und der Höhenschnittpunkt $H$ auf einer Geraden, der
sogenannten Eulerschen Geraden, liegen.
Zeigen Sie weiterhin, dass der Inkreismittelpunkt $W$ nicht auf der Eulerschen Geraden liegt.

Der Umkreismittelpunkt ist der Schnittpunkt aller Mittelsenkrechten der Dreiecksseiten, d.h. der Geraden, die durch den Mittelpunkt der Dreiecksseiten
verlaufen und senkrecht zu der Seite liegen.
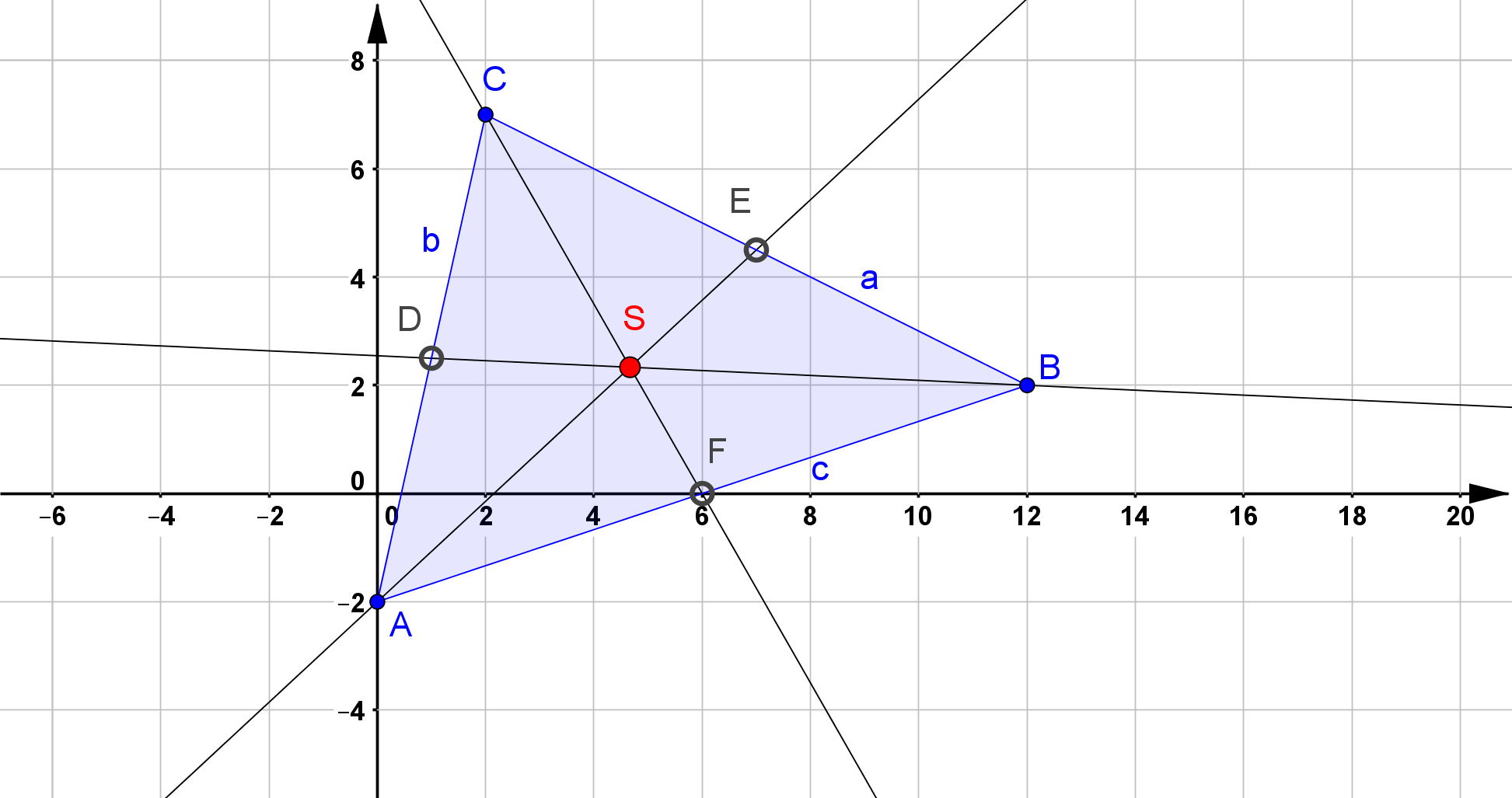
Der Flächenschwerpunkt ist der Schnittpunkt der drei Seitenhalbierenden, d.h. der Geraden, die durch den Seitenmittelpunkt und dem gegenüberliegenden
Eckpunkt verlaufen.
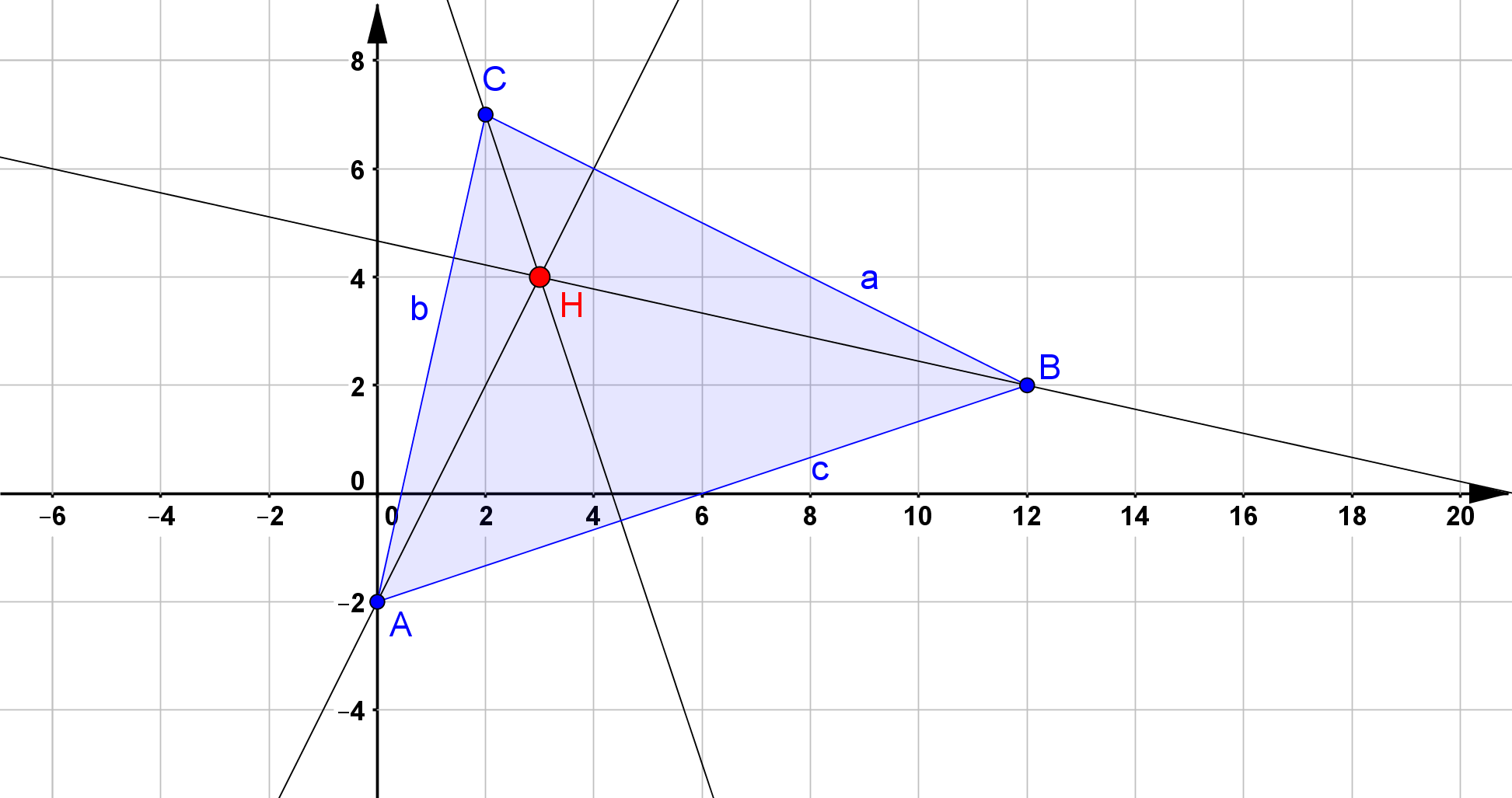
Der Höhenschnittpunkt ist der Schnittpunkt der drei Höhen auf den Dreiecksseiten, d.h. der Geraden, die durch den Eckpunkt verlaufen und senkrecht
zu der gegenüberliegenden Seite liegen.
Zunächst werden die Geradengleichungen für die Dreiecksseiten $a$ und $b$ ermittelt. Die Gleichung für $c$ wird nicht benötigt, da der
Schnittpunkt schon durch zwei der Mittelsenkrechten bestimmt werden kann. Dazu werden die Seitenmittelpunkte $D$ und $E$ gebraucht.
\begin{align}
g_a: \qquad \frac{y - y_1}{x - x_1} &= \frac{y_1 - y_2}{x_1 - x_2} \qquad \qquad \text{Zwei-Punkte-Form} \\
\frac{y - 2}{x - 12} &= \frac{2 - 7}{12 - 2} \\
y - 2 &= \frac{-5}{10} \cdot (x - 12) \\
y - 2 &= - \frac{1}{2} x + 6 \\
y &= - \frac{1}{2} x + 8
\end{align}
Steigung der Geraden senkrecht zur Seite $a$
\begin{align}
m_2 &= - \frac{1}{m_1} \\
m_\bot &= - \frac{1}{- \frac{1}{2}} \\
m_\bot &= 2
\end{align}
Mittelpunktskoordinaten der Seite $a$
\begin{align}
x_E &= \frac{12 + 2}{2} \qquad&\qquad y_E &= \frac{2 + 7}{2} \\
x_E &= 7 \qquad&\qquad y_E &= \frac{9}{2} \\
& \qquad \qquad \qquad E \left( 7/\frac{9}{2} \right)
\end{align}
Geradengleichung der Mittelsenkrechten zu $a$
\begin{align}
y - y_1 &= m \cdot (x - x_1) \\
y - \frac{9}{2} &= 2 \cdot (x - 7) \\
y_{\bot a} &= 2 x - \frac{19}{2}
\end{align}
\begin{align} g_b: \qquad \frac{y - (-2)}{x - 0} &= \frac{-2 - 7}{0 - 2} \qquad \qquad \qquad \qquad \qquad \\ y + 2 &= \frac{-9}{-2} \cdot x \\ y &= \frac{9}{2} x - 2 \end{align} Steigung der Geraden senkrecht zur Seite $b$ \begin{align} m_\bot &= - \frac{1}{\frac{9}{2}} \\ m_\bot &= - \frac{2}{9} \end{align} Mittelpunktskoordinaten der Seite $b$ \begin{align} x_D &= \frac{0 + 2}{2} \qquad&\qquad y_D &= \frac{-2 + 7}{2} \\ x_D &= 1 \qquad&\qquad y_D &= \frac{5}{2} \\ & \qquad \qquad \qquad D \left( 1/\frac{5}{2} \right) \end{align} Geradengleichung der Mittelsenkrechten zu $b$ \begin{align} y - \frac{5}{2} &= - \frac{2}{9} \cdot (x - 1) \\ y_{\bot b} &= - \frac{2}{9} x + \frac{49}{18} \end{align}
Bestimmung der Koordinaten für $M$ \begin{align} y_{\bot a} &= y_{\bot b} \\ 2 x - \frac{19}{2} &= - \frac{2}{9} x + \frac{49}{18} \\ \frac{20}{9} x &= \frac{220}{18} \\ x_M &= \frac{11}{2} \\ \\ y_M &= 2 \cdot \frac{11}{2} - \frac{19}{2} \\ y_M &= \frac{3}{2} \\ \\ M & \left( \frac{11}{2} / \frac{3}{2} \right) \qquad \qquad \leftarrow \qquad \text{Umkreismittelpunkt} \end{align}
Mit den bereits gefundenen Mittelpunkten der Seiten $a$ und $b$, nämlich $D \left( 1/\frac{5}{2} \right)$ für die Seite $b$ und
$E \left( 7/\frac{9}{2} \right)$ für die Seite $a$ können in Kombination mit dem jeweils der Seite gegenüberliegenden Eckpunkten
($A$ bzw. $B$) die Geradengleichungen der Seitenhalbierenden gebildet werden.
\begin{align}
\frac{y - y_1}{x - x_1} &= \frac{y_1 - y_2}{x_1 - x_2} \\
y &= \frac{y_1 - y_2}{x_1 - x_2} \cdot (x - x_1) + y_1
\end{align}
\begin{align}
y_{DB} &= \frac{\frac{5}{2} - 2}{1 - 12} \cdot (x - 1) + \frac{5}{2} \qquad&\qquad y_{EA} &= \frac{\frac{9}{2} - (-2)}{7 - 0} \cdot (x - 7) + \frac{9}{2} \\
y_{DB} &= - \frac{1}{22} x + \frac{56}{22} \qquad&\qquad y_{EA} &= \frac{13}{14} x - 2
\end{align}
\begin{align}
y_{DB} &= y_{EA} \\ \\
- \frac{1}{22} x + \frac{56}{22} &= \frac{13}{14} x - 2 \\
\frac{300}{308} x &= \frac{100}{22} \\
x &= \frac{14}{3} \\
y &= \frac{13}{14} \cdot \frac{14}{3} - 2 \\
y &= \frac{7}{3} \\ \\
S & \left( \frac{14}{3} / \frac{7}{3} \right) \qquad \qquad \leftarrow \qquad \text{Flächenschwerpunkt}
\end{align}
Mit der Kenntnis der Steigung einer senkrecht zu $a$ bzw. $b$ liegenden Geraden, $m_{\bot a}= 2$ und $m_{\bot b} = - \frac{2}{9}$, dem entsprechenden,
der Seite $a$ und $b$ gegenüberliegenden Eckpunkt und der Punkt-Steigungs-Form lassen sich die Geradengleichungen der Höhen auf den Seiten $a$
und $b$ bestimmen.
\begin{align}
y - y_1 = m \cdot (x - x_1)
\end{align}
\begin{align}
y_{ha} &= 2 \cdot \left( x - 0 \right) + (-2) \qquad&\qquad y_{hb} &= - \frac{2}{9} \cdot \left( x - 12 \right) + 2 \\
y_{ha} &= 2 x - 2 \qquad&\qquad y_{hb} &= - \frac{2}{9} x + \frac{14}{3}
\end{align}
\begin{align}
y_{ha} &= y_{hb} \\ \\
2 x - 2 &= - \frac{2}{9} x + \frac{14}{3} \\
\frac{20}{9} x &= \frac{20}{3} \\
x &= 3 \\
y &= 2 \cdot 3 - 2 \\
y &= 4 \\ \\
H & \left( 3 / 4 \right) \qquad \qquad \leftarrow \qquad \text{Höhenschnittpunkt}
\end{align}
Mit dem Einsetzen der Koordinaten der drei Punkte kann die Gerade bestimmt werden, bzw. es kann überprüft werden, ob die drei Punkte auf einer Geraden liegen. Mit der Zwei-Punkte-Form kann eine Geradengleichung ermittelt werden, wenn zewei Punktkoordinaten eingesetzt werden. Werden drei Punktkoordinaten eingesetzt, erfolgt eine Überprüfung. Eingesetzt werden der Punkt $M$ mit den Koordinaten $x / y$, der Punkt $S$ mit den Koordinaten $x_1 / y_1$ und der Punkt $H$ mit den Koordinaten $x_2 / y_2$. \begin{align} \frac{\frac{3}{2} - \frac{7}{3}}{\frac{11}{2} - \frac{14}{3}} &= \frac{\frac{7}{3} - 4}{\frac{14}{3} - 3} \\\\ \frac{\frac{9}{6} - \frac{14}{6}}{\frac{33}{6} - \frac{28}{6}} &= \frac{\frac{7}{3} - \frac{12}{3}}{\frac{14}{3} - \frac{9}{3}} \\\\ \frac{- \frac{5}{6}}{\frac{5}{6}} &= \frac{- \frac{5}{3}}{\frac{5}{3}} \\\\ -1 &= -1 \end{align} Die Gleichung entspricht der Wahrheit, also liegen alle drei Punkte auf einer Geraden.
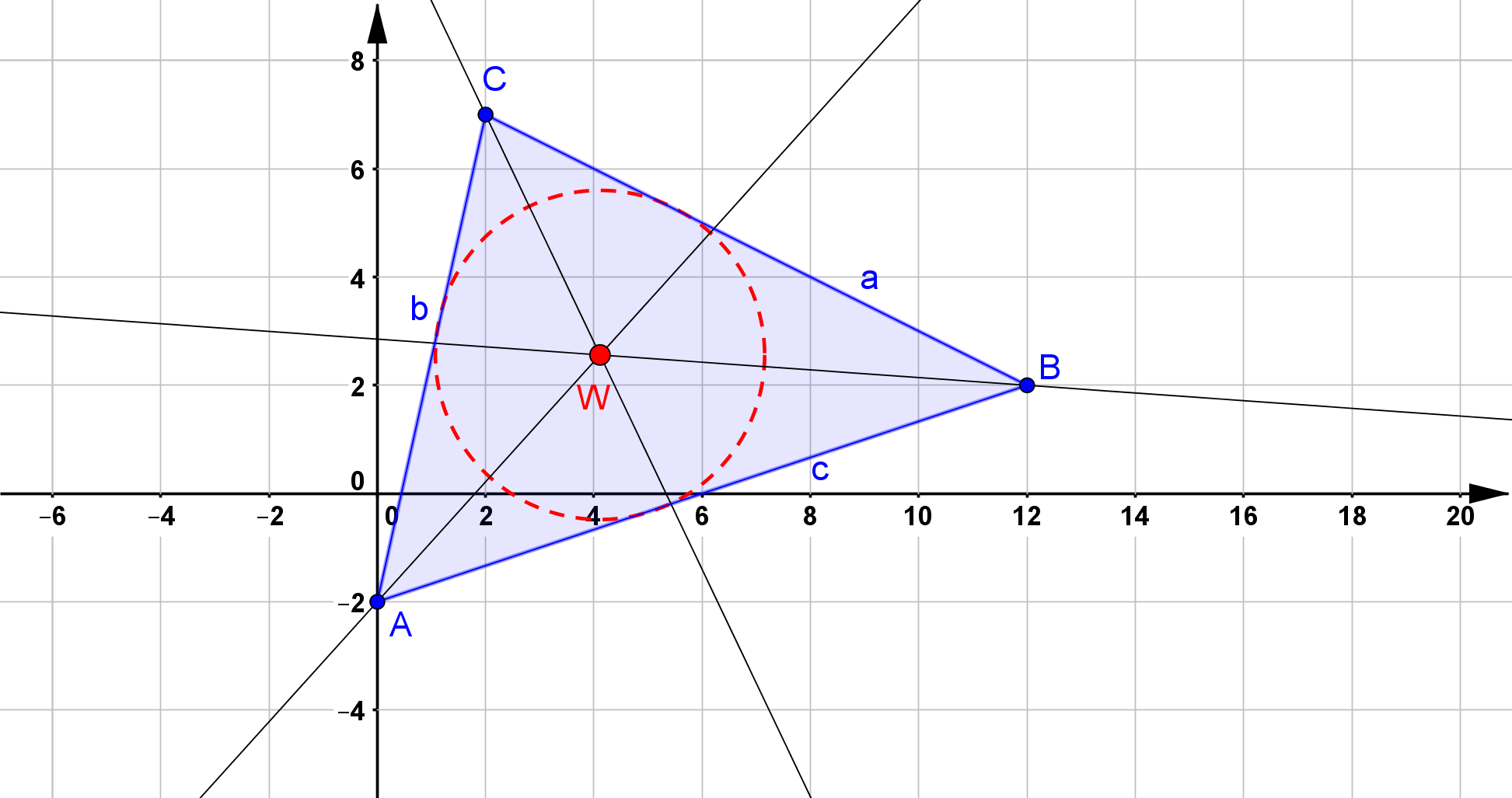
Der Inkreismittelpunkt ist der Schnittpunkt der drei Winkelhalbierenden.
Zunächst soll die Winkelhalbierende durch den Punkt $A$ bestimmt werden.
Die Steigung der Seite $b$ beträgt $m_b = \frac{9}{2}$, die der Seite
$c$ kann mit $m_c = \frac{1}{3}$ ermittelt werden. Das ergibt jeweils den Steigungswinkel $\alpha_b = 77,47$° und $\alpha_c = 18,43$°. Der Mittelwert
des Steigungswinkels ist damit $\alpha_A = 47,95$°. Damit folgt die Steigung $m_A = 1,1$.
Mit der Punkt-Steigungs-Form ergibt sich:
\begin{align}
y_A &= 1,1 \cdot (x - 0) - 2 \\
y_A &= 1,1 x - 2
\end{align}
Analog für die Gerade durch den Punnkt $C$: Mit $m_a = - \frac{1}{2}$ erhält man $\alpha_a = -26,57$°. Zusammen mit $\alpha_b = 77,47$° erhält man den mittleren Steigungswinkel durch $C$: $\alpha_C = 25,45$°. Da es aber immer zwei Schnittwinkel zwischen zwei Geraden gibt, muss überlegt werden, ob das Ergebnis hier sinnvoll ist. Dadurch kommt man zu der Erkenntnis, dass die Winkelhalbierende durch den Punkt $C$ eine negative Steigung und damit einen negativen Steigungswinkel haben muss. Hier muss also $\alpha_C = 25,45\text{°} - 90\text{°} = -64,55$° gelten und damit $m_C = -2,1$. \begin{align} y_C &= -2,1 \cdot (x - 2) + 7 \\ y_C &= -2,1 x + 11,1 \end{align}
\begin{align} y_A &= y_C \\\\ 1,1 x - 2 &= - 2,1 x + 11,1 \\ 3,2 x &= 13,1 \\ x &= 4,09 \\ y &= 1,1 \cdot 4,09 - 2 \\ y &= 2,5 \\\\ W \left( 4,09 / 2,5 \right) \end{align}
Mit $W (x/y)$, $S (x_1/y_1)$ und $H (x_2/y_2)$ folgt:
\begin{align}
\frac{2,5 - \frac{7}{3}}{4,09 - \frac{14}{3}} &= \frac{\frac{7}{3} - 4}{\frac{14}{3} - 3} \\\\
\frac{0,17}{-0,58} &= \frac{- \frac{5}{3}}{\frac{5}{3}} \\\\
-0,29 &= -1
\end{align}
Die Aussage ist unwahr, also liegt $W$ nicht auf der Geraden durch $S$ und $H$. Damit ist $W$ auch nicht Bestandteil der Eulerschen Geraden.
© mondbrand MMXIX