Nullstellenbestimmung
Die Bestimmung von Nullstellen ist eine der wichtigeren Aufgaben beim Umgang mit funktionellen Zusammenhängen. Daher wird ihr eine
besondere Aufmerksamkeit zuteil.
Nullstellen können u.a. auf die folgenden Weisen bestimmt werden:
Nullstellenbestimmung durch Äquivalenzumformung
Kommt die Variable in der Funktionsgleichung in nur einer einzigen Form vor, z.B. als $x$ oder als $x^3$, können die Nullstellen durch
die Äquivalenzumformung bestimmt werden.
\begin{align}
f(x) &= m \cdot x + b &\qquad &f(x) = 0 \\ \\
0 &= m \cdot x + b &\qquad &\vert -b \\
-b &= m \cdot x &\qquad &\vert :m \\
\frac{-b}{m} &= x
\end{align}
\begin{align}
f(x) &= a \cdot x^2 + c &\qquad &f(x) = 0 \\ \\
0 &= a \cdot x^2 + c &\qquad &\vert -c \\
-c &= a \cdot x^2 &\qquad &\vert :a \\
\frac{-c}{a} &= x^2 &\qquad &\vert \sqrt{} \\
\pm \sqrt{\frac{-c}{a}} &= x
\end{align}
\begin{align}
f(x) &= a \cdot \sin(x - \pi) &\qquad &f(x) = 0 \\ \\
0 &= a \cdot \sin(x - \pi) &\qquad &\vert :a \\
0 &= \sin(x - \pi) &\qquad &\vert \sin^{-1}() \\
\sin^{-1}(0) &= x - \pi &\qquad &\vert + \pi \\
\pi &= x
\end{align}
Mit der Lösung $x = \pi$ erhält man
eine Lösung. Für
alle Lösungen muss man berücksichtigen, wann der Sinus eines Ausdrucks Null wird.
Das ist der Fall, erstens, für Null, zweitens für $\pi$, wie die berechnete Lösung zeigt, und drittens für alle ganzzahligen Vielfachen von $\pi$, also
z.B. $2 \pi$ oder $5 \pi$. Alle Lösungen für die Nullstellen lauten somit:
$$
x = k \cdot \pi \qquad \qquad k \in \mathbb{Z}
$$
\begin{align}
f(x) &= a \cdot b^x + c &\qquad &f(x) = 0 \\ \\
0 &= a \cdot b^x + c &\qquad &\vert -c \\
-c &= a \cdot b^x &\qquad &\vert :a \\
\frac{-c}{a} &= b^x &\qquad &\vert \log_b () \\
\log_b \left(\frac{-c}{a}\right) &= x
\end{align}
Beispiele
\begin{align}
f(x) &= 2 \cdot x + 4 &\qquad &f(x) = 0 \\ \\
0 &= 2 \cdot x + 4 &\qquad &\vert -4 \\
-4 &= 2 \cdot x &\qquad &\vert :2 \\
-2 &= x
\end{align}
\begin{align}
f(x) &= - x^2 + 1 &\qquad &f(x) = 0 \\ \\
0 &= - x^2 + 1 &\qquad &\vert -1 \\
-1 &= - x^2 &\qquad &\vert \cdot (-1) \\
1 &= x^2 &\qquad &\vert \sqrt{} \\
\pm 1 &= x
\end{align}
Nullstellenbestimmung durch die pq-Formel
Die pq-Formel löst allgemeine quadratische Gleichungen in der folgenden Form:
$$
x^2 + px + q = 0
$$
Die Lösungen sind dann:
$$
x_1 = - \frac{p}{2} + \sqrt{\left(\frac{p}{2}\right)^2 - q} \\ \\
x_2 = - \frac{p}{2} - \sqrt{\left(\frac{p}{2}\right)^2 - q}
$$
Der Graph einer quadratischen Funktion kann zwei, eine oder gar keine Nullstelle aufweisen. Entscheidend für die Anzahl der Nullstellen ist der
Term unter der Wurzel, d.h. $\left(\frac{p}{2}\right)^2 - q$. Es können die folgenden Fälle unterschieden werden:
\begin{align}
\left(\frac{p}{2}\right)^2 - q > 0 \qquad &\rightarrow \qquad \text{zwei Nullstellen} \\ \\
\left(\frac{p}{2}\right)^2 - q = 0 \qquad &\rightarrow \qquad \text{eine (doppelte) Nullstelle} \\ \\
\left(\frac{p}{2}\right)^2 - q < 0 \qquad &\rightarrow \qquad \text{keine Nullstellen}
\end{align}
Bei einer doppelten Nullstelle berührt der Graph die $x$-Achse, während bei einer einfachen Nullstelle die Achse geschnitten wird.
Beispiele
\begin{align}
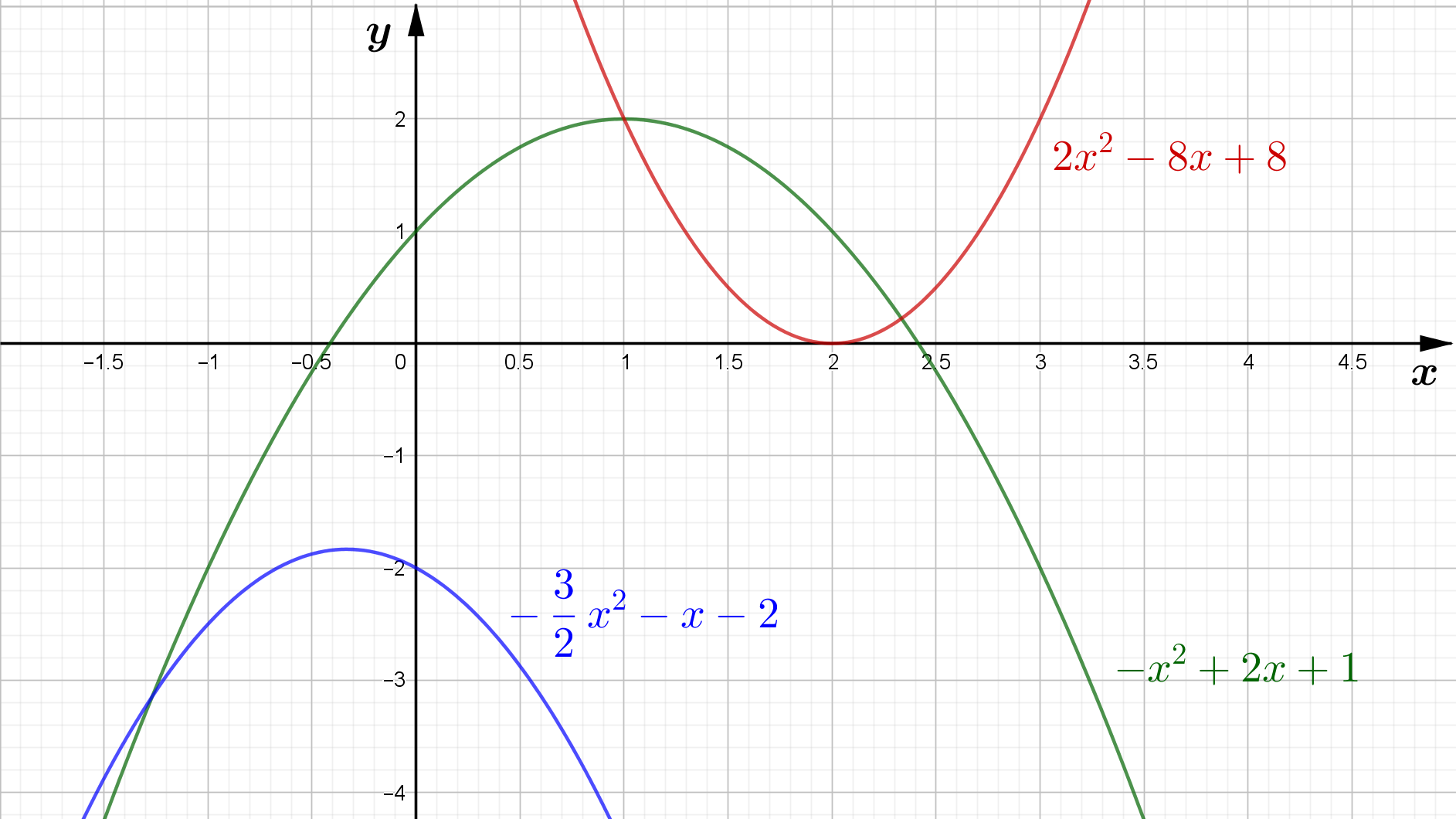
f(x) &= - x^2 + 2x + 1 &\qquad &f(x) = 0 \\ \\
0 &= - x^2 + 2x + 1 &\qquad &\vert \cdot (-1) \\ \\
0 &= x^2 - 2x - 1 &\qquad &\vert p = -2 \; ; \; q = -1 \\ \\
x_{1,2} &= - \frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right)^2-(-1)} \\ \\
x_{1,2} &= 1 \pm \sqrt{1 + 1} \\ \\
x_{1,2} &= 1 \pm 1,41 \\ \\
x_1 = 2,41 \qquad &; \qquad x_2 = - 0,41
\end{align}
\begin{align}
f(x) &= 2 x^2 - 8x + 8 &\qquad &f(x) = 0 \\ \\
0 &= 2 x^2 - 8x + 8 &\qquad &\vert : 2 \\ \\
0 &= x^2 - 4x + 4 &\qquad &\vert p = -4 \; ; \; q = 4 \\ \\
x_{1,2} &= - \frac{-4}{2} \pm \sqrt{\left(\frac{-4}{2}\right)^2- 4} \\ \\
x_{1,2} &= 2 \pm \sqrt{4 - 4} \\ \\
x_{1,2} &= 2 \pm 0 \\ \\
x_{1,2} &= 2
\end{align}
\begin{align}
f(x) &= - \frac{3}{2} x^2 - x - 2 &\qquad &f(x) = 0 \\ \\
0 &= - \frac{3}{2} x^2 - x - 2 &\qquad &\vert \cdot \left( - \frac{2}{3} \right) \\ \\
0 &= x^2 + \frac23 x + \frac43 &\qquad &\vert p = \frac23 \; ; \; q = \frac43 \\ \\
x_{1,2} &= - \frac{\frac23}{2} \pm \sqrt{\left(\frac{\frac23}{2}\right)^2- \frac43} \\ \\
x_{1,2} &= - \frac13 \pm \sqrt{\frac19 - \frac{12}{9}} \\ \\
x_{1,2} &= - \frac13 \pm \sqrt{ - \frac{11}{9}} \\ \\
x_{1,2} &= \{ \} \qquad \rightarrow \qquad \text{keine Nullstellen}
\end{align}
Nullstellenbestimmung durch Ausklammern


