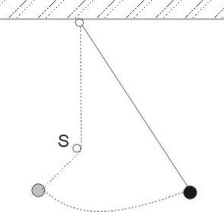
30 cm unter dem Aufhängepunkt eines 50 cm langen Fadenpendels befindet sich ein fester Stift S, an den
sich der Faden während des Schwingens vorübergehend anlegt.
Bestimmen Sie die Anzahl der Schwingungen des Pendels in einer Minute.
Eine ganze Schwingung setzt sich aus zwei halben Schwingungen zusammen. Einmal die Schwingung auf der rechten
Seite mit der Fadenlänge 50 cm und einmal auf der linken Seite mit der Fadenlänge 20 cm.
Damit wird auch die gesamte Periodendauer aus zwei halben Periodendauern gebildet:
$$
T = \frac{T_r}{2} + \frac{T_l}{2}
$$
Für die jeweiligen Periodendauern rechts,$T_r$, und links, $T_l$, gilt die Formel
$T = 2 \pi \cdot \sqrt{\frac{l}{g}}$.
Daraus folgt also:
\begin{align}
T &= \frac{T_r}{2} + \frac{T_l}{2} \\
T &= \frac{2 \pi \cdot \sqrt{\frac{l_r}{g}}}{2} + \frac{2 \pi \cdot \sqrt{\frac{l_l}{g}}}{2} \\
T &= \pi \cdot \sqrt{\frac{l_r}{g}} + \pi \cdot \sqrt{\frac{l_l}{g}} \\
T &= \pi \cdot \left( \sqrt{\frac{l_r}{g}} + \sqrt{\frac{l_l}{g}} \right) \\
T &= \frac{\pi}{\sqrt{g}} \cdot \left( \sqrt{l_r} + \sqrt{l_l} \right) \\
T &= \frac{\pi}{\sqrt{9,81 \, \frac{\text{m}}{\text{s}^2}}} \cdot \left( \sqrt{0,5 \text{ m}} + \sqrt{0,2 \text{ m}} \right) \\
T &= 1,158 \text{ s}
\end{align}
Damit kann die Frequenz der Schwingung bestimmt werden:
$$
f = \frac{1}{T} = \frac{1}{1,158 \text{ s}} = 0,86 \text{ Hz}
$$
Bei 0,86 Schwingungen pro Sekunde führt das Pendel in einer Minute 51,6 Schwingungen aus.