An einer Feder mit der Federkonstanten $D = 198,2 \, \frac{\text{N}}{\text{m}}$ hängt ein Körper mit der
Masse $m = 2 \text{ kg}$. Die Amplitude der Schwingung beträgt 10 cm.
a) Berechnen Sie die Frequenz der Schwingung.
Zum Zeitpunkt $t = 0$ befindet sich der Körper in der Gleichgewichtsposition.
b) Geben Sie die Schwingungsgleichung an.
c) Berechnen Sie die maximale Geschwindigkeit der Schwingung. Zu welchem Zeitpunkt wird sie das erstemal
erreicht?
d) Bestimmen Sie die Kraft, mit der der Körper maximal beschleunigt wird.
Eine beliebige Federschwingung wird durch $s(t) = 2 \text{ cm} \cdot sin ( \pi \text{ s}^{-1} t - \frac{\pi}{2})$
beschrieben.
a) Berechnen Sie die Auslenkung nach 0,7 s. Zu welchem Zeitpunkt ist die Auslenkung wieder so groß?
b) Bestimmen Sie Geschwindigkeit und Beschleunigung nach 0,7 s.
c) Geben Sie den Zeitpunkt an, zu dem die Geschwindigkeit 4 cm/s beträgt.
Ein Körper der Masse 2,5 kg hängt an einem 1,4 m langen Faden.
a) Berechnen Sie die Periodendauer, wenn sich das Pendel in Mitteleuropa befindet.
b) An einem anderen Ort misst man mit demselben Pendel die Periodendauer 2,4 s. Bestimmen Sie den dortigen
Ortsfaktor.
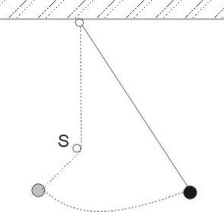30 cm unter dem Aufhängepunkt eines 50 cm langen Fadenpendels befindet sich ein fester Stift S, an den
sich der Faden während des Schwingens vorübergehend anlegt.
Bestimmen Sie die Anzahl der Schwingungen des Pendels in einer Minute.