Eine Schwingung ist jede periodisch wiederkehrende Veränderung einer physikalischen Größe. Beispiele dafür sind etwa das Hin- und Herschwingen eines Pendels einer Standuhr, der Verlauf des Sonnenstands über dem Horizont oder auch der Verlauf von Aktienindizes.
Bei vielen Schwingungsvorgängen kann man die Veränderung der Größe mathematisch beschreiben. Um diese Beschreibungsmöglichkeiten wird es hier im Wesentlichen gehen.
Um Schwingungen möglichst allgemein beschreiben zu können, betrachtet man zunächst eine Masse $m$, die an einer Feder hängt und um einen
bestimmten Betrag nach unten ausgelenkt wird. Es handelt sich um ein sogenanntes Federpendel, das
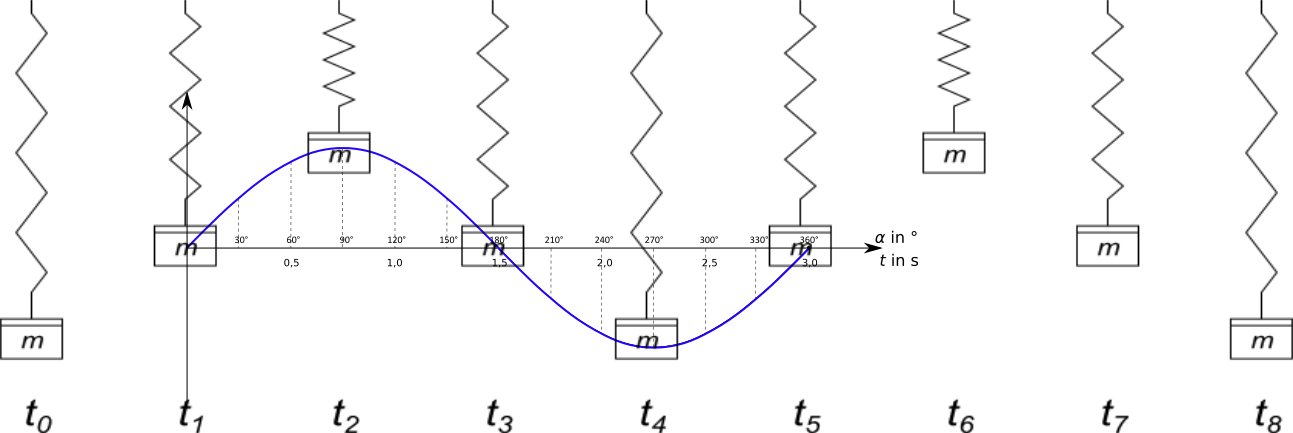
klassische Modell für Schwingungen. In der Abbildung ist ein solcher Schwinger zu verschiedenen Zeitpunkten des Schwingungsvorgangs zu sehen.
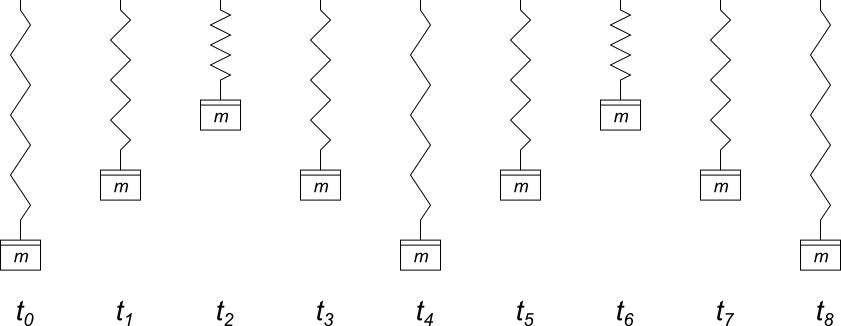
In dieser Abbildung wird deutlich, dass es bei der mathematischen Beschreibung von Schwingungen nicht nur um die tatsächliche Größe, hier die Auslenkung, selbst geht, sondern auch um die Veränderung der Größe.
Die Größe zum Zeitpunkt $t_0$ ist die maximale Auslenkung der Masse nach unten. Zu diesem Zeitpunkt verändert sich die Auslenkung nicht (siehe dazu die Definition der momentanen Änderungsrate aus der Mathematik). Damit ist jede wiederkehrende maximale Auslenkung nach unten gleichwertig und beschreibt den gleichen Zustand der Schwingung.
Die maximale Auslenkung nach oben ist nicht der gleiche Schwingungszustand, weil die Änderung der Auslenkung hier zwar auch Null ist (Maximum und
Minimum sind beides Extrempunkte), die Auslenkung selbst aber einen anderen Wert besitzt.
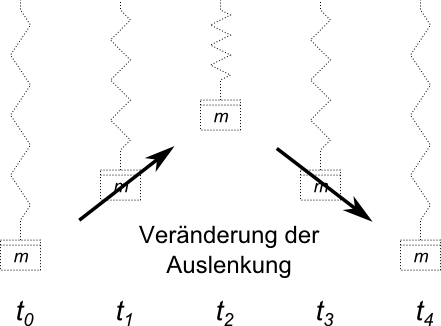
Die Auslenkung der Masse zu den Zeitpunkten $t_1$ und $t_3$ ist die gleiche. Zum Zeitpunkt $t_1$ verändert sich die Auslenkung aber nach oben, d.h. die Masse wird nach oben verschoben, zum Zeitpunkt $t_3$ verändert sie sich nach unten, die Masse wird demzufolge nach unten verschoben. Damit wird zu den beiden Zeitpunkten ein unterschiedlicher Schwingungszustand beschrieben. Erst zum Zeitpunkt $t_5$ wird derselbe Zustand wie zum Zeitpunkt $t_1$ beschrieben.
Der Zustand einer Schwingung wird also durch die Größe und durch die Änderung der Größe beschrieben.
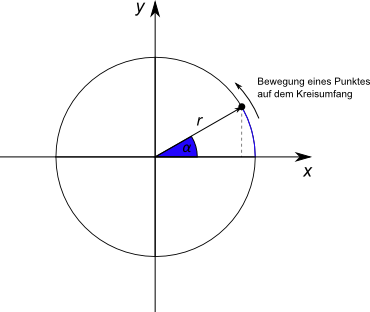Der Einheitskreis ist zunächst ein Kreis mit dem Radius $r = 1$. Mit Hilfe des Einheitskreises kann die oben schon zu erkennende Schwingungsbewegung
mathematisch beschrieben werden, indem die Position eines Punktes während eines Umlaufs um den Kreis in ein Koordinatensystem projiziert wird.
Der Kreis befindet sich in einem $x-y-$Koordinatensystem, die projizierte Bewegung wird in einem $t-y-$Koordinatensystem dargestellt.
Betrachtet wird nur die $y-$Position des Punktes in Abhängigkeit von der Zeit. Bei der Bewegung des Punktes handelt es sich um eine gleichförmige Bewegung mit einer konstanten Geschwindigkeit. Es wird in gleichen Zeitabschnitten immer der gleiche Winkel $\alpha$ zurückgelegt.
Die $y-$Position des Punktes ist gleichbedeutend mit der Gegenkathete des Winkels $\alpha$. Mit dem Radius $r = 1$ folgt direkt:
$$
y = \sin \alpha
$$
Weil $\alpha$ von $t$ abhängt, haben wir insgesamt die Abhängigkeit $y(t)$. Wird diese Abhängigkeit in einem Diagramm dargestellt, folgt:
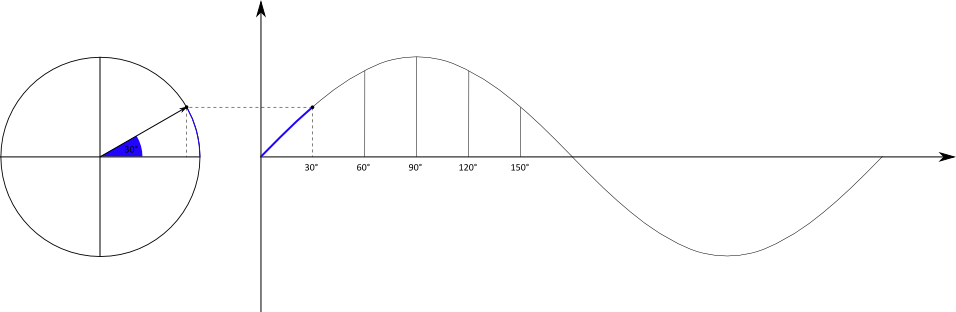
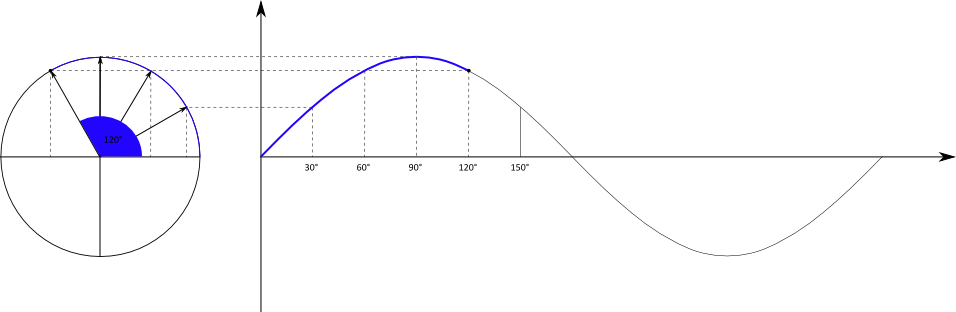
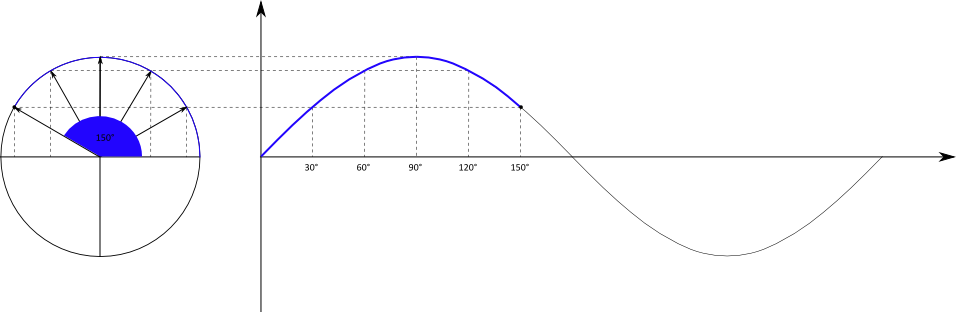
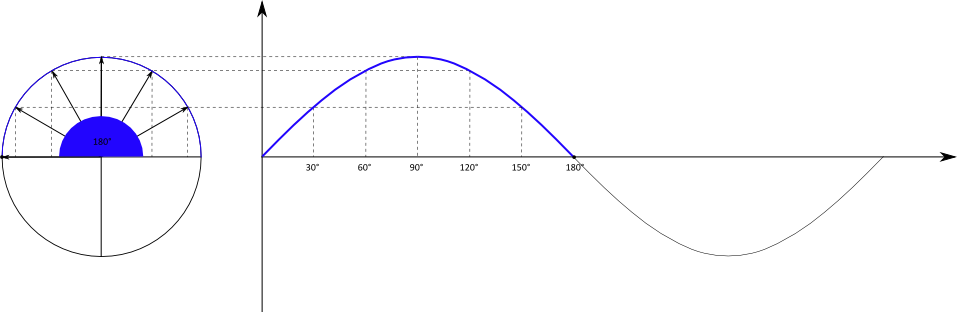
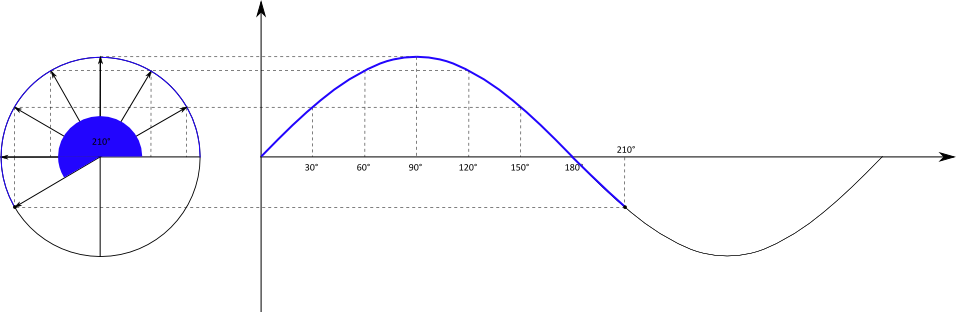
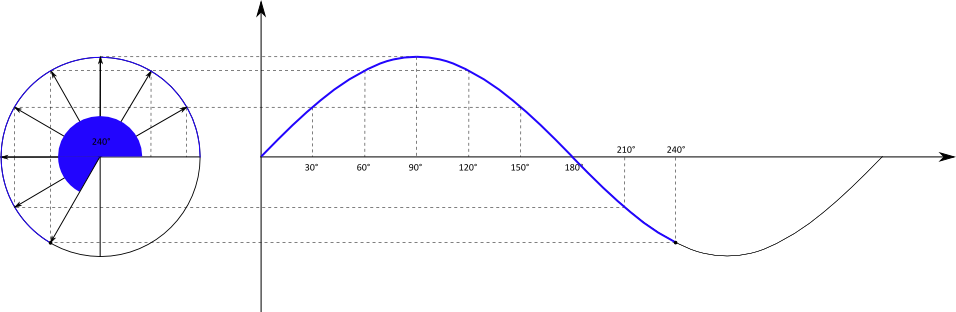
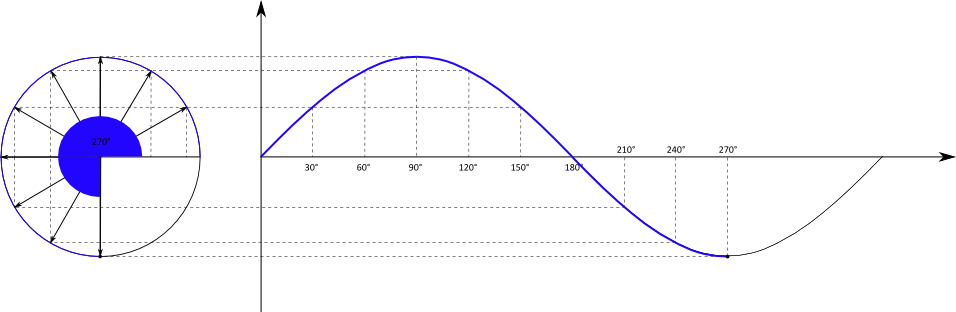
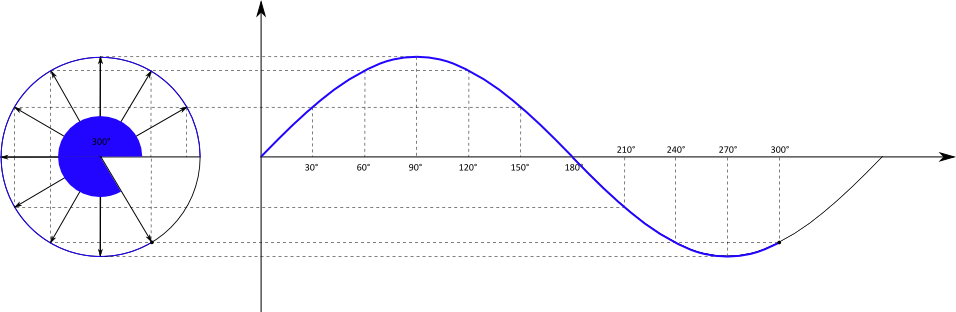
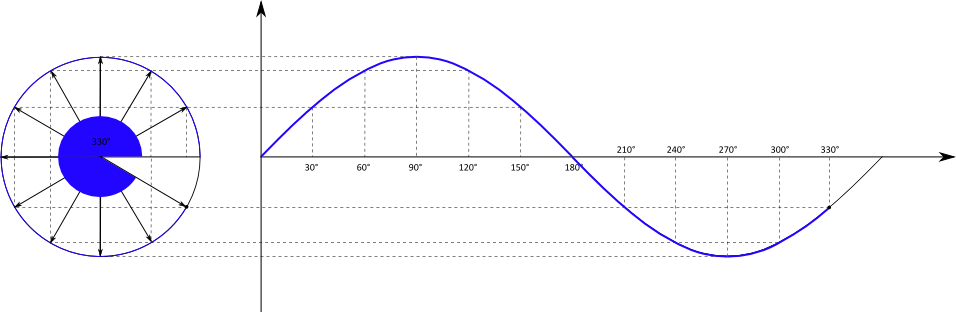
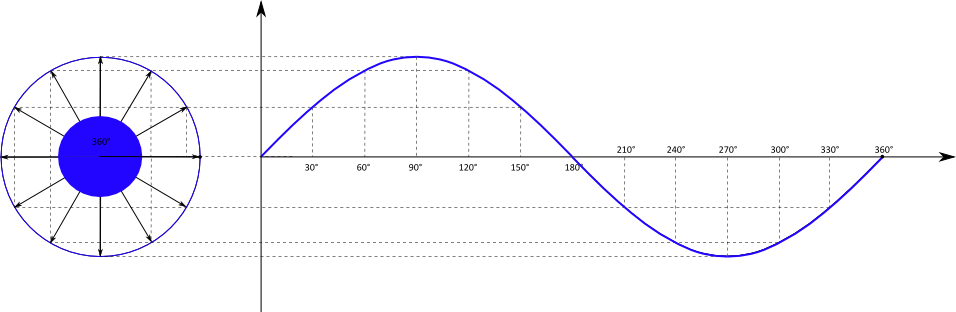
Die Kreisbewegung wird also übertragen in einen sinusförmigen Funktionsgraph. Die Zeitachse des Graphen ist dabei entweder tatsächlich die laufende
Zeit in der Einheit Sekunde, oder der überstrichene Winkel bei der Kreisbewegung.
Wird beispielsweise der Kreis in drei Sekunden einmal umrundet, kann die $x-$Achse entweder die Zeitspanne von Null bis drei Sekunden oder
den Winkel von 0° bis 360° umfassen.
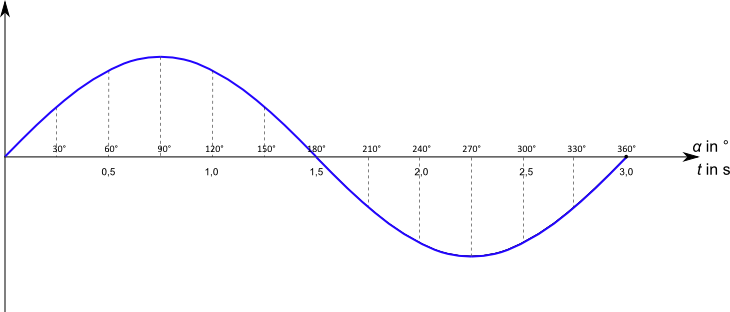
Die am Anfang gezeigte Auslenkung eines Federpendels entspricht genau dieser Sinusfunktion und damit der $y-$Position der Bewegung im Einheitskreis..
Der Umfang eines Kreises wird durch $U = \pi \cdot d = 2 \pi \cdot r$ berechnet. Mit dem Radius des Einheitskreise von $r = 1$ folgt für den Umfang
$$
U = 2 \pi
$$
Damit gilt
$$
2 \pi = 360^\circ
$$
Die Länge $2 \pi$ ist die Länge des Umfanges des Einheitskreises oder die Länge des Kreisbogens für einen vollen Kreisumfang. Für jeden beliebigen
Winkel $\alpha$ ist die Länge des Kreisbogens:
$$
b = 2 \pi \frac{\alpha}{360^\circ}
$$
Damit haben wir eine dritte Möglichkeit, die $x-$Achse des Diagramms zu bezeichnen: das Bogenmaß.
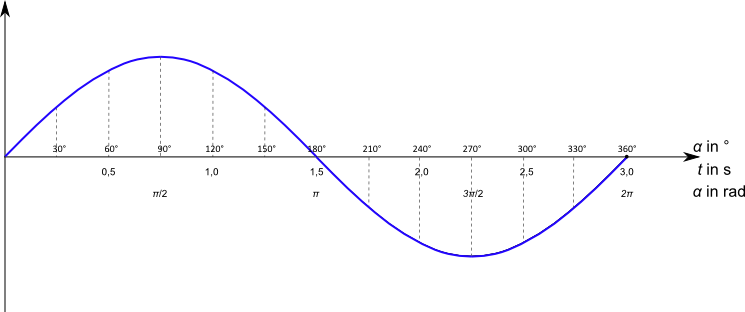
Zukünftig wird die Größe auf der $x-$Achse entweder die Zeit $t$ oder das Bogenmaß sein.
Typischerweise lautet der Funktionsterm folgendermaßen:
$$
y(t)=\hat{y} \cdot sin (\omega t + \varphi_0)
$$
Der Term $y(t)$ wird zeitabhängige Elongation genannt. Er beschreibt die Auslenkung des schwingenden Körpers zu jeder Zeit $t$.
Da der Sinus immer nur zwischen -1 und 1 hin- und herpendelt, zeigt die Angabe $\hat{y}$ die maximale Auslenkung bei der vorliegenden
Schwingung an. Diese maximale Auslenkung wird Amplitude genannt.
$\omega$ ist die Winkelgeschwindigkeit, d.h. die Geschwindigkeit, in der sich der Winkel im Einheitskreis ändert. Dabei gilt:
$$
\omega = \frac{2 \pi}{T}
$$
$T$ als Schwingungsdauer oder Periodendauer ist die Zeit für genau einen Umlauf, also für die Strecke des Einheitskreisumfangs
$U= 2 \pi$. Wegen $T = \frac{1}{f}$ gilt auch:
$$
\omega = 2 \pi f
$$
wobei $f$ die Frequenz der Schwingung ist. Diese beschreibt, wieviele Schwingungen in einer Sekunde stattfinden. Damit bekommt
$\omega$ eine weitere Bezeichnung: Kreisfrequenz
Die Phasenverschiebung $\varphi_0$ beschreibt das Verhalten des Funktionsgraphen zum Zeitpunkt $t = 0$. Damit wird der Graph nach links (+ $\varphi_0$)
oder nach rechts (- $\varphi_0$) verschoben.
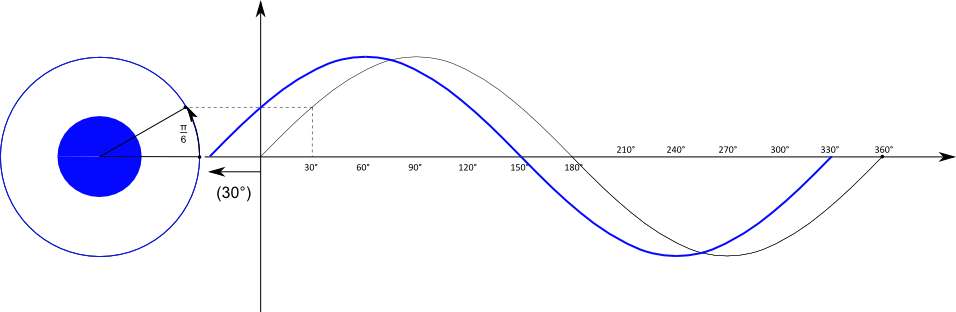
Die Verschiebung nach links, wie in der Abbildung, bedeutet, dass ein Punkt auf dem Einheitskreis gegen den Uhrzeigersinn, also mathematisch
positiv, verschoben wird. Zu beachten ist dabei, dass die Phasenverschiebung im Bogenmaß angegeben wird.
Mit der Umlaufzeit $T = 3 \text{ s}$ aus dem Beispiel oben würde sich hier eine Phasenverschiebung von:
\begin{align}
2 \pi \;&\hat{=}\; 3 \text{ s} \\
\frac{\pi}{6} \;&\hat{=}\; 0,25 \text{ s} \\
\varphi_0 \;&= \frac{\pi}{6}
\end{align}
Damit ist der Funktionsterm
$$
y(t) = \hat{y} \cdot sin \left( \frac{2 \pi}{3 \text{ s}} t + \frac{\pi}{6} \right)
$$
Für die Elongation gilt der Funktionsterm
$$
y(t) = \hat{y} \cdot sin(\omega t + \varphi_0) \qquad \leftarrow \qquad \text{Elongation}
$$
Die Geschwindigkeit einer Bewegung ist die Ableitung des Ortes nach der Zeit:
\begin{align}
v(t) &= y'(t) \\
v(t) &= \omega \hat{y} \cdot cos(\omega t + \varphi_0) \qquad \leftarrow \qquad \text{Geschwindigkeit}
\end{align}
Der Ausdruck $\omega \hat{y}$ ist dabei die maximale Geschwindigkeit $\hat{v}$ der Schwingungsbewegung.
Die Ableitung der Geschwindigkeit ergibt die Beschleunigung:
\begin{align}
a(t) &= v'(t) = y''(t) \\
a(t) &= - \omega^2 \hat{y} \cdot sin ( \omega t + \varphi_0) \qquad \leftarrow \qquad \text{Beschleunigung}
\end{align}
Auch hier bezeichnet der Ausdruck $\omega^2 \hat{y}$ die maximale Beschleunigung $\hat{a}$, die während der Schwingung wirkt.
Für die zeitabhängige wirkende Kraft auf den schwingenden Körper gilt demnach:
\begin{align}
F(t) &= m \cdot a(t) \\
F(t) &= - m \omega^2 \hat{y} \cdot sin ( \omega t + \varphi_0) \qquad \leftarrow \qquad \text{Kraft}
\end{align}
Für eine beispielhafte Schwingung mit $\hat{y} = 0,6 \text{ cm}$, $\omega = \pi \text{ s}^{-1}$ und $\varphi_0 = \frac{\pi}{6}$ ergeben sich
die folgenden Funktionsgraphen für $s(t)$, $v(t)$ und $a(t)$ (Die Elongation in $y$-Richtung wird allgemein mit der Bewegungsgröße $s$ bezeichnet):
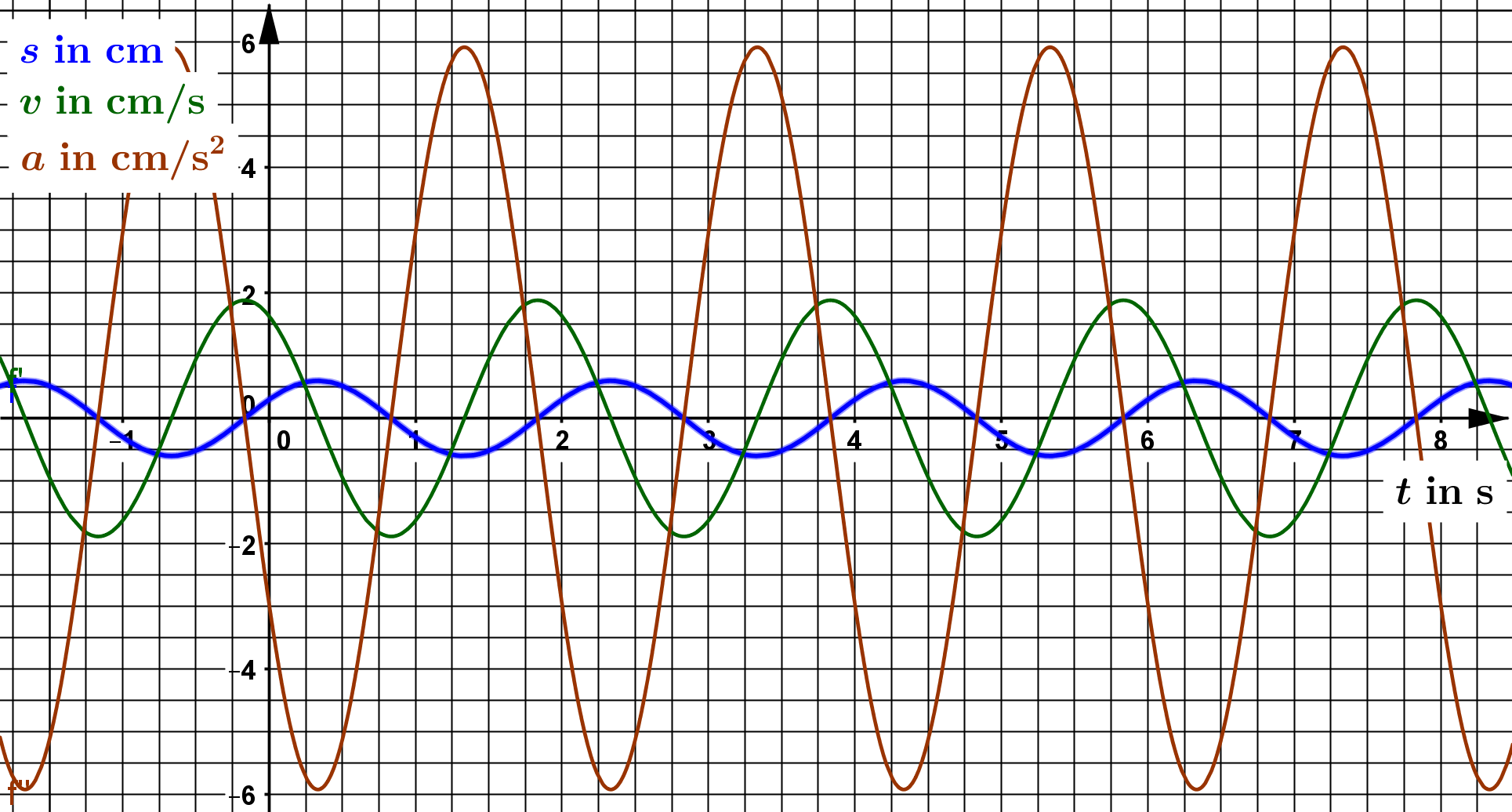
Die maximale Geschwindigkeit der Schwingung ist damit $\hat{v} = \omega \hat{y} = \pi \cdot 0,6 \, \frac{\text{cm}}{\text{s}} = 1,885 \, \frac{\text{cm}}{\text{s}}$ und die maximale
Beschleunigung berechnet sich zu $\hat{a} = \omega^2 \hat{y} = \pi^2 \cdot 0,6 \, \frac{\text{cm}}{\text{s}^2} =5,922 \, \frac{\text{cm}}{\text{s}^2}$.
Anhand der Verläufe der jeweiligen Graphen kann man erkennen, dass die Geschwindigkeit der Schwingung immer Null ist, wenn der schwingende Körper gerade seine Amplitude (positive und negative) erreicht. Zur gleichen Zeit ist auch die Beschleunigung maximal mit dem entsprechenden Vorzeichen, negativ bei einer positiven Auslenkung und positiv bei einer negativen Auslenkung. Entsprechendes gilt für die Kraft, die in die gleiche Richtung wirkt wie die Beschleunigung.
Die maximale Geschwindigkeit wird erreicht, wenn der schwingende Körper gerade seine Gleichgewichtsposition durchläuft. Dort sind auch die Beschleunigung und die Kraft Null (Gleichgewicht - Kräfte heben sich auf - keine Beschleunigung - Änderung der Geschwindigkeit ist Null - Maximum oder Minimum der Geschwindigkeit).
Die Gesetzmäßigkeiten für Elongation, Geschwindigkeit, Beschleunigung und Kraft gelten für sogenannte harmonische Schwingungen. Eine Schwingung ist dann harmonisch, wenn sie durch eine Sinusfunktion beschrieben werden kann, was der Fall ist, wenn es sich um ein Federpendel handelt. Ein Federpendel, wie es ganz oben zu sehen ist, schwingt harmonisch.
Eine weitere Formulierung lautet, dass eine Schwingung harmonisch ist, wenn die Rückstellkraft proportional zur aktuellen Auslenkung ist. Beim Federpendel gelten die Kraftgesetze der Feder, d.h. im elastischen Bereich gilt: $$ F = - D \cdot s $$ wobei der Proportionalitätsfaktor $D$ als Federkonstante oder Federhärte bezeichnet wird.
Es folgt: \begin{align} F(t) &= - m \omega^2 \hat{y} \cdot sin ( \omega t + \varphi_0) \\ &\qquad \qquad y(t) = \hat{y} \cdot sin ( \omega t + \varphi_0) \\ &\qquad \qquad D = m\omega^2 \\ F(t) &= - D \cdot y(t) \\ F(t) &= - D \cdot s \end{align} Aus $D = m\omega^2$ folgt: $\omega = \sqrt{\frac{D}{m}}$. Es gilt weiterhin $\omega = \frac{2 \pi}{T}$, woraus insgesamt folgt: $$ T = 2 \pi \sqrt{\frac{m}{D}} $$ für die Periodendauer einer harmonischen Schwingung eines Federpendels.
Beim Federpendel ist der Zusammenhang zwischen Kraft und Auslenkung proportional; die Richtung der Kraft ist stets entweder parallel oder
antiparallel zur Bewegungsrichtung. Handelt es sich um ein sogenanntes Fadenpendel, gilt dieser Zusammenhang nicht mehr uneingeschränkt.
Die Auslenkung $s$ eines Fadenpendels wird durch den waagerechten Abstand von der Gleichgewichtslage festgelegt (wie auch beim Federpendel).
Die Bewegungsrichtung des Pendelkörpers ist aber zu jedem Zeitpunkt tangential zum Kreis mit dem Radius $l$, der Länge des Pendels. In der Abbildung ist die Kraft, die die Rückstellkraft für die Schwingungsbewegung darstellt, mit $F_R$ bezeichnet. Sie wirkt immer tangential zur Kreisbahn der Pendelbewegung.
Wenn die Rückstellkraft in derselben Richtung wirkte wie $s$, gäbe es kein Problem, denn dann würde gelten, dass $F_R$ proportional zu $s$ wäre. Da sie aber immer entlang der aktuellen Richtung $b$ wirkt, müssen $s$ und $b$ miteinander verglichen werden. Bei dem Vergleich wird deutlich, dass sich $s$ und $b$ nur sehr wenig voneinander unterscheiden, solange der Winkel $\alpha$ klein bleibt, d.h. wenn die Auslenkung $s$ klein bleibt. Klein heißt hier, dass $\alpha < 10^\circ$ bleiben sollte. Zur Kleinwinkelnäherung mit der Vergleichstabelle: hier.
Also gilt: \begin{align} F_R &= F_G \cdot \sin(\alpha) \\ F_R &= m \cdot g \cdot \sin(\alpha) \\ F_R &= m \cdot g \cdot \frac{s}{l} \\ F_R &= \frac{m \cdot g}{l} \cdot s \end{align} Dabei wird folgendes berücksichtigt: Die Bogenlänge $b$ eines Kreisbogens ist $b = \alpha \cdot l$, mit $\alpha$ im Bogenmaß. Weiterhin gilt, wegen der Kleinwinkelnäherung, $b \approx s$ und $sin (\alpha) = \frac{s}{l}$.
Für Winkel kleiner als 10° gilt: Das Fadenpendel beschreibt eine harmonische Schwingung.
Der Proportionalitätsfaktor $\frac{mg}{l}$ kann mit der Federkonstanten $D$ gleichgesetzt werden. Dieser Faktor definiert die Geometrie des Pendels, so wie die Federkonstante die Feder definiert. Setzt man $D = \frac{mg}{l}$ in die Formel für die Periodendauer des Federpendels ein, folgt: \begin{align} T &= 2 \pi \sqrt{\frac{m}{D}} \qquad \qquad \leftarrow \qquad \text{Periodendauer Federpendel} \\ T &= 2 \pi \sqrt{\frac{ml}{mg}} \\ T &= 2 \pi \sqrt{\frac{l}{g}} \qquad \qquad \leftarrow \qquad \text{Periodendauer Fadenpendel} \end{align}
Für den Federschwinger kann die folgende Überlegung angewendet werden:
In der Gleichgewichtsposition und bei Stillstand, d.h. wenn die Feder zwar
durch die angehängte Masse belastet aber noch nicht in Schwingung gebracht wird, ist die Energie gleich Null. Wird die Masse ausgelenkt, z.B. nach unten,
dehnt sich die Feder um den Betrag $s$ und die in der Feder gespeicherte Energie beträgt $E = \frac{1}{2} \cdot D \cdot s^2$, mit der Federkonstanten
$D$. In diesem Zustand ist die Geschwindigkeit der Schwingung gleich Null. Damit ist auch die kinetische Energie gleich Null und die Gesamtenergie
besteht lediglich aus der Federenergie, ist also $E = \frac{1}{2} \cdot D \cdot \hat{s}^2$ mit der Amplitude $\hat{s}$.
Beim Durchgang durch die Gleichgewichtslage ist die Geschwindigkeit maximal und die Federauslenkung ist gleich
Null. Die kinetische Energie ist somit auch maximal und die Federenergie ist gleich Null. Die Gesamtenergie besteht also nur aus der kinetischen
Energie, $E = \frac{1}{2} \cdot m \cdot \hat{v}^2$ mit der Geschwindigkeitsamplitude $\hat{v}$.
Den Ausdruck für die kinetische Energie lässt sich umformen: \begin{align} E &= \frac{1}{2} \cdot m \cdot \hat{v}^2 \\ E &= \frac{1}{2} \cdot m \cdot \left( \omega \cdot \hat{s} \right)^2 \\ E &= \frac{1}{2} \cdot m \cdot \omega^2 \cdot \hat{s}^2 \\ E &= \frac{1}{2} \cdot D \cdot \hat{s}^2 \end{align}
Für jeden Zwischenzustand gilt: Die Gesamtenergie ist zu jeder Zeit die Summe aller Einzel-Energien. Es kann also zu jeder beliebigen Zeit $t$ die folgende Rechnung gemacht werden: \begin{align} E &= E_{kin}(t) + E_{Fed}(t) \\ E &= \frac{1}{2} \cdot m \cdot v(t)^2 + \frac{1}{2} \cdot D \cdot s(t)^2 \\ &\qquad \qquad \qquad \text{mit:}\, v(t) = \omega \hat{s} \cdot cos (\omega t + \varphi_0) \, \text{und} \, s(t) = \hat{s} \cdot sin (\omega t + \varphi_0) \\ E &= \frac{1}{2} \cdot m \cdot \left( \omega \hat{s} \right)^2 \cdot cos^2(\omega t + \varphi_0) + \frac{1}{2} \cdot D \cdot \hat{s}^2 \cdot sin^2 (\omega t + \varphi_0) \\ &\qquad \qquad \qquad \text{mit:}\, m \omega^2 = D \\ E &= \frac{1}{2} \cdot D \cdot \hat{s}^2 \cdot cos^2(\omega t + \varphi_0) + \frac{1}{2} \cdot D \cdot \hat{s}^2 \cdot sin^2 (\omega t + \varphi_0) \\ E &= \frac{1}{2} \cdot D \cdot \hat{s}^2 \cdot \left( cos^2 (\omega t + \varphi_0) + sin^2 (\omega t + \varphi_0) \right) \\ &\qquad \qquad \qquad \text{mit:}\, cos^2 (\omega t + \varphi_0) + sin^2 (\omega t + \varphi_0) = 1 \\ E &= \frac{1}{2} \cdot D \cdot \hat{s}^2 \end{align} Die Energie in einer Federschwingung ist immer $E = \frac{1}{2} \cdot D \cdot \hat{s}^2$.
Für das Fadenpendel gilt folgendes:
In der Ruhelage ist die kinetische und die potentielle Energie gleich Null. Wird das Pendel ausgelenkt, wird eine maximale Höhe $h$ erreicht. Die
kinetische Energie ist an den Umkehrpunkten Null. Beim Durchgang durch die Gleichgewichtsposition gilt wieder, dass die kinetische Energie
maximal und die potentielle Energie Null ist. Für alle Zwischenzustände ist die Summe aus kinetischer und potentieller Energie
gleich der Gesamtenergie.
Für den Durchgang durch die Gleichgewichtsposition gilt:
\begin{align}
E &= E_{kin} = \frac{1}{2} \cdot m \cdot \hat{v}^2 \\
E &= \frac{1}{2} \cdot m \cdot \omega^2 \cdot \hat{s}^2 \\
E &= \frac{1}{2} \cdot \frac{mg}{l} \cdot \hat{s}^2
\end{align}
Für die maximale Auslenkung gilt:
\begin{align}
h_{max} &= l - l \cdot \cos(\alpha_{max}) \\
h_{max} &= l (1 - \cos(\alpha_{max})) \\ \\
E &= m \cdot g \cdot h_{max} \\
E_{pot} &= m \cdot g \cdot l (1 - \cos(\alpha_{max}))
\end{align}
Für $\alpha_{max}$ gilt wiederum die Beziehung:
$$
\sin(\alpha_{max}) = \frac{\hat{s}}{l}
$$
Zu jedem Zeitpunkt der Schwingung gilt:
\begin{align}
E &= E_{kin}(t) + E_{pot}(t) \\
E &= \frac{1}{2} \cdot m \cdot v^2(t) + m \cdot g \cdot l (1 - \cos(\alpha(t))) \\
E &= \frac{1}{2} \cdot m \cdot \omega^2 \cdot \hat{s}^2 \cdot \cos^2(\omega t) + m \cdot g \cdot l (1 - cos(\alpha(t)))
\end{align}
Wobei auch hier wieder gilt:
$$
\sin(\alpha(t)) = \frac{\hat{s} \cdot \sin(\omega t)}{l}
$$
© mondbrand MMXX