Was sind Funktionen, warum gibt es sie und was machen sie?

Nimmt man eine bestimmte Menge an Menschen, z.B. eine Schulklasse mit 23 Schülern, kann man eine Liste aufstellen, in der jeder Schüler mit seiner Schuhgröße eingetragen ist. Dabei ist klar, dass jeder Schüler nur eine Schuhgröße hat, jede Schuhgröße aber von mehreren Schülern getragen werden kann. Kann - nicht muss!

Wenn diese Schüler ihre Schuhe auf einen Haufen werfen und zwei Schüler mit der gleichen Schuhgröße zufällig auch noch die gleichen Schuhe haben, ist es vollkommen unklar, welche Schuhe zu welchem Schüler gehören.

Jeder Schüler hat also genau eine Schuhgröße, d.h. jedem Schüler kann genau eine Schuhgröße zuugeordnet werden. Das ist es, um was es bei der Betrachtung von Funktionen geht: eindeutige Zuordnungen.

Jedem Element einer Definitionsmenge wird genau ein Element einer Wertemenge zugeordnet. Mathematisch: $$ S \in D \rightarrow G \in W $$

Im Prinzip kann man Jedem Alles zuordnen:

Die oben genannten Beispiele stellen spezielle Fälle, Einzelfälle, dar. In der Mathematik versucht man nun, solche Zuordnungen zu verallgemeinern. Dabei werden Zahlen anderen Zahlen zugeordnet. So entstehen allgemeine Zuordnungsvorschriften, die für eine Vielzahl von Anwendungen genutzt werden können.

Die Bedeutung der Zuordnung kann die aus der oberen Tabelle sein (Schüler $\rightarrow$ Schuhgröße), aber auch z.B. die Zuordnung Schüler $\rightarrow$ Körpertemperatur (Schüler 3 hat Fieber und sollte zu Hause bleiben...) oder Lehrer $\rightarrow$ Alter.

Bei einer Zuordnung nennt man die Menge der $x$ aus dem Definitionsbereich die freien Variablen, die Menge der $y$ aus dem Wertebereich die abhängigen Variablen der Zuordnung.

Für die Mathematik ist es von besonderem Interesse zu erfahren, wie sich die abhängige Variable verändert, wenn sich die freie Variable ändert. Verdoppelt sich $y$, wenn sich $x$ verdoppelt? Oder halbiert sich $y$ in diesem Fall? Oder steigt es mal an und fällt dann wieder ab?
Ein weiterer interessanter Punkt ist, das man etwas über das Verhalten der Zuordnung in Fall eines $x$-Wertes ausgesagen kann, wenn man die Zuordnung für den Vorgänger des $x$-Wertes kennt. Das führt letztendlich dazu, dass es für alle $x$-Werte eine einzige Zuordnungsvorschrift gibt, die die jeweiligen $y$-Werte berechnen kann.

Um das Verhalten der abhängigen Variablen darzustellen, werden beide Variablen in ein Koordinatensystem eingetragen. Im kartesischen Koordinatensystem werden die freien Variablen $x$ auf der waagerechten $x$-Achse (Abzisse) und die abhängigen Variablen $y$ auf der senkrechten $y$-Achse (Ordinate) eingetragen. Möchte man nun das Verhalten von $y$ beschreiben, wird die $x$-Achse von links nach rechts "abgegangen".

Hier beginnt der Berg, mit steigendem $x$ anzusteigen. Mit weiter steigendem $x$ steigt der Berg stärker an, bevor er später abfällt und erneut ansteigt, usw.

Wenn in der Mathematik die Betrachtung von Einzelpunkten und die Verbindungen zwischen Einzelpunkten überführt wird in die Betrachtung von Intervallen aus dem Definitions- und Wertebereich, können Zuordnungen durch Linien, also durch Funktionsverläufe oder Funktionsgraphen deutlich gemacht werden.
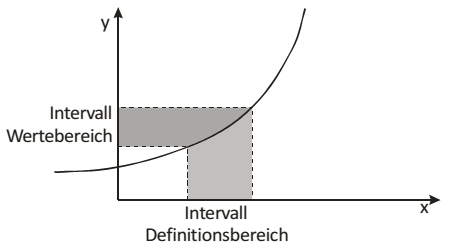Dieser Übergang von Einzelpunkten auf Linien hat damit zu tun, dass der Abstand zwischen den Punkten so klein gemacht wird, dass er von Null nicht mehr zu unterscheiden ist. Damit erhält man unendlich viele Punkte, und zwar auf jedem noch so kleinen Intervall, was einer Linie entspricht.

Wie weiter oben schon beschrieben, kann die Mathematik nur Zuordnungen berechnen und bearbeiten, die nicht chaotisch oder zufällig verlaufen. Die Zuordnung Schüler $\rightarrow$ Schuhgröße ist daher nicht sinnvoll, da mit der Kenntnis der Schuhgröße von Schüler Nr. 3 nicht klar ist, welche Schuhgröße Schüler Nr. 4 hat. Genau das aber sind die Anforderungen an eine mathematisch sinnvolle Zuordnung, die für alle $x$-Werte den zugehörigen $y$-Wert berechnen kann.

Diese Zuordnungsvorschrift sieht im Grunde immer so aus: $$ y = \text{irgendetwas mit} \; x $$ Dieses "irgendetwas mit x" ist dann eine Regel, die für jedes $x$ ein $y$ herausgibt. Das kann man sich als "black box", als Maschine vorstellen, die jedes $x$ frisst und dafür ein $y$ ausspuckt.

Diese Maschine ist sehr gefrässig und absolut geistlos, denn es frisst alle $x$ aus dem Definitionsbereich, manchmal unendlich viele. Aber sie frisst wahllos und ohne Unterschied, und ab und zu kann sie sich auch verschlucken, dann spuckt sie ihre Innereien / Zahnräder aus, z.B. wenn sie durch Null dividieren musste. Das kann sehr eklig werden...

Weiter oben wurde geschrieben, dass die Zuordnungen eindeutig sein müssen. Dann gibt es für jedes $x$ ein eindeutiges $y$. Ein Beispiel wäre die Zuordnung Schüler $\rightarrow$ Schuhgröße, denn jeder Schüler hat nur eine Schuhgröße. Die Zuordnung Schuhgröße $\rightarrow$ Schüler wäre nicht eindeutig, denn jede Schuhgröße kann von mehreren Schülern getragen werden. Es wäre also nicht klar, welcher Schüler gemeint wäre, wenn eine bestimmte Schuhgröße genannt wird.

Funktionen erkennt man grafisch daran, dass sie:

Verboten wären also folgende Graphen:

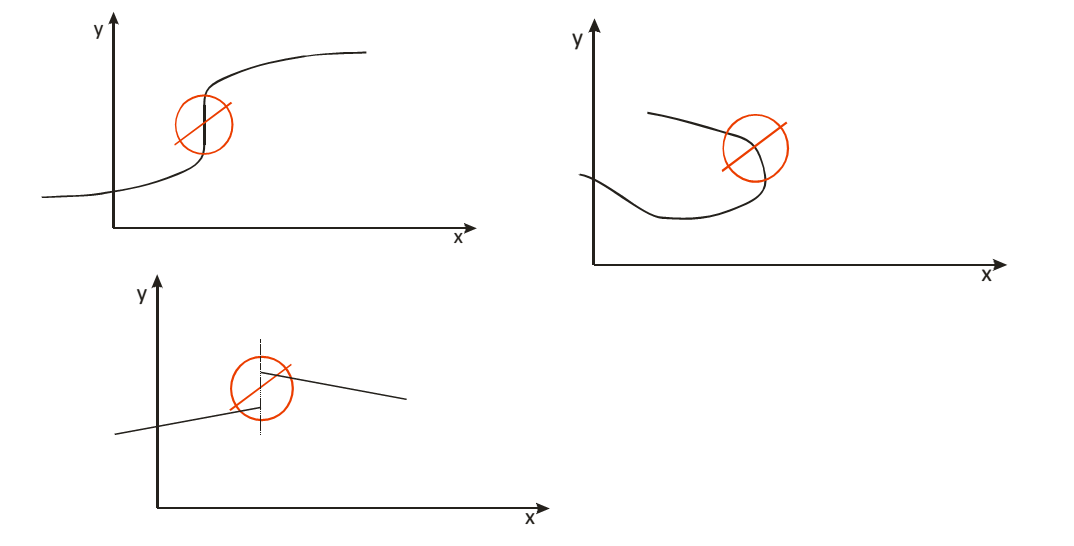
Ein einzelner Punkt im Koordinatensystem besteht immer aus zwei Koordinaten: $$ P ( x/y) $$ Ein Punkt $P$ mit der $x$-Koordinate $x$ und der $y$-Koordinate $y$ liegt genau dann auf dem Graphen der Funktion $f$, wenn die Koordinaten die Funktionsgleichung erfüllen: $$ y = f(x) $$

Es gibt unterschiedliche Typen von Funktionen, die sich aufgrund ihrer Eigenschaften im Erscheinungsbild im Koordinatensystem unterscheiden. Wichtige Funktionstypen sind:

© mondbrand MMXIX