

 Jeder Körper und jede Materie besteht aus Atomen. Das haben schon die Griechen vor etwa 2500 Jahren vermutet. Demokrit, der etwa von
460 - 371 v.Chr. lebte, ist derjenige, auf den die Idee des atomaren Aufbaus der Materie zurückgeführt wird. Seine Vorstellungen
gehen allerdings auf seinen Lehrer Leukipp zurück, der davon ausging, dass die Materie aus kleinsten Teilchen bestehen muss.
Jeder Körper und jede Materie besteht aus Atomen. Das haben schon die Griechen vor etwa 2500 Jahren vermutet. Demokrit, der etwa von
460 - 371 v.Chr. lebte, ist derjenige, auf den die Idee des atomaren Aufbaus der Materie zurückgeführt wird. Seine Vorstellungen
gehen allerdings auf seinen Lehrer Leukipp zurück, der davon ausging, dass die Materie aus kleinsten Teilchen bestehen muss.
Leukipp und Demokrit gelten als die Begründer des Atomismus, nach dem die Welt aus leerem Raum und aus Materie besteht. Das Werden
und Vergehen der Materie und deren Veränderungen kann durch Umordnung der Atome im leeren Raum durch Bewegung, durch Zusammenstöße, Vereinigungen
und Trennungen erklärt werden.
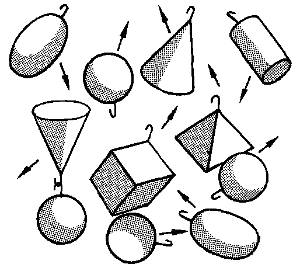
In der Abildung ist dargestellt, wie sich Demokrit die Atome vorstellte. Unterschiedliche Formen sollten die verschiedenen Materieeigenschaften hervorbringen, Haken sollten die Vereinigungen mehrerer Atome bewerkstelligen.
Im zweiten Jahrhundert wird Demokrit so zitiert:
Denn nur durch Konvention (oder Übereinkunft, Gewöhnung) existiert Farbe; bitter und süß sind Konvention, doch die Realität besteht nur aus Atomen und Leere.
Um 1803 entwickelte John Dalton sein Atommodell, das sich von dem Demokrits im wesentlichen dadurch unterschied, dass die verschiedenen Elemente durch Atome mit unterschiedlichen Massen gebildet werden. Die Atome selbst wurden weiterhin als kleine, feste und nicht teilbare Kugeln betrachtet.
100 Jahre später, also 1903, beschrieb Joseph John Thompson ein neues Atommodell. Nach diesem Modell bestehen die Atome aus einer Masse positiver Ladung, die das gesamte Atom ausfüllt. Innerhalb dieser positiven Masse sind einzelne Elektronen verteilt (Rosinenkuchen-Modell). Thompson deutete die Elektronen als die Träger der Atommasse, wohingegen die positive Ladung als masselos angesehen wurde.
1909 wurde der bekannte Rutherford'sche Streuversuch durchgeführt. Dessen Ergebnisse konnten mit dem Atommodell von Thompson nicht erklärt werden. Als Verfeinerung dessen entwickelte Rutherford 1911 sein Modell. Das Atom besteht aus einem Kern, in dem fast die gesamte Masse konzentriert und der positiv geladen ist. Die Elektronen als Träger der negativen Ladung bewegen sich um den Kern herum. Um aber einige experimentelle Ergebnisse zu erklären, reichte das Rutherford'sche Modell nicht aus. Es wurde 1913 von Niels Bohr weiter verfeinert.
Das Atommodell nach Niels Bohr sieht so aus, dass es einen positiven Atomkern und eine Atomhülle aus Elektronen gibt. Im Gegensatz zum Rutherford'schen Modell dürfen die Elektronen nur innerhalb bestimmter Bahnen um den Kern kreisen. Auf diesen Bahnen bewegen sie sich ohne Energieverlust (was der klassischen Mechanik widerspricht) und sie können durch Absorption bzw. Emission von bestimmten Energiemengen zwischen diesen Bahnen wechseln.(⇒ zum Bohrschen Atommodell)
1919 bzw. 1932 schließlich wurden die Kernbausteine (Nukleonen) Proton bzw. Neutron nachgewiesen. Das Proton wurde als Träger der positiven Ladung bezeichnet, das Neutron wurde als ungeladen beschrieben. Beide Bausteine sollten ungefähr die gleiche Masse besitzen.
Die positive Ladung eines Protons und die negative Ladung eines Elektrons sind dem Betrag nach gleich groß. Es gilt für den Ladungsbetrag:
$$e = 1,602176565 \cdot 10^{-19} \, \text{C}$$
$e$ bezeichnet dabei die Elementarladung, d.h. den kleinstmöglichen Ladungsbetrag. Jede vorhandene Ladung setzt sich aus ganzzahligen
Vielfachen der Elementarladung zusammen.(⇒ Millikan-Versuch)
Ein Elektron hat demnach die Ladung $q_{Elektron} = - \, e$.
Die Ladung wird i.A. mit $q$ bezeichnet. Die Einheit ist das Coulomb. $$ \text{Ladung} \; q \\ \left[ q \right] = 1 \, \text{C} $$
Kommen gleich viele positive und negative Ladungen zusammen, neutralisieren sie sich. Beispielsweise besteht ein Atom aus gleich vielen Elektronen und
Protonen. Nach außen ist das Atom neutral, die einzelnen Teilchen sind aber dennoch geladen.
Für die Ladung gilt ein Erhaltungssatz, wie auch für Masse, Energie oder Impuls: Ladung geht nicht verloren, sie kann nicht verbraucht oder erzeugt werden.
Elektrische Ladungen werden als das Fundament der Elektrizitätslehre bezeichnet.
Strom ist fließende oder sich bewegende Ladung. Die Stromstärke wird dabei definiert als der Quotient aus der Ladungsmenge und dem Zeitintervall, in dem
sich die Ladung durch den Leiterquerschnitt bewegt. Das Formelzeichen für die Stromstärke ist das $I$, abgeleitet von Intensität des Stromflusses.
Die Bezeichnung $q$ für die Ladung kommt vom lateinischen quantum. Die Einheit der Stromstärke ist das Ampere, eine der Basiseinheiten des
SI-Systems.
$$
\text{Stromstärke} \, I \\
\left[I\right] = 1 \, \text{A}
$$
 In dem Zylinderstück mit der Länge $v \cdot \Delta t$ befinden sich die Elektronen, die in dem Zeitintervall $\Delta t$ die dunkel markierte
Fläche durchfliegen werden.
In dem Zylinderstück mit der Länge $v \cdot \Delta t$ befinden sich die Elektronen, die in dem Zeitintervall $\Delta t$ die dunkel markierte
Fläche durchfliegen werden.
Die oben genannte Definition der Stromstärke führt auf diese Gleichung:
\begin{align}
I &= \frac{q}{\Delta t} \qquad \text{oder} \\ \\
q &= I \cdot \Delta t
\end{align}
Daraus folgt für die Einheiten:
$$
1 \text{C} = 1 \text{A} \cdot \text{s}
$$
Materie besteht aus Atomen und damit aus Ladungen. Im Allgemeinen ist die Anzahl der negativen und positiven Ladungen gleich, so dass die Materie neutral ist. Verändert man aber nun die Anzahl der Elektronen in einem Körper, indem man einige hinzufügt, wird der Körper negativ geladen. Werden in einem anderen Körper Elektronen entfernt, wird dieser Körper positiv geladen. Kommen sich die beiden Körper, z.B. zwei Kugeln, näher, entsteht zwischen den Elektronen, die im negativ geladenen Körper zu viel sind, und den Stellen, wo im positiv geladenen Körper die Elektronen waren, ein elektrisches Feld.
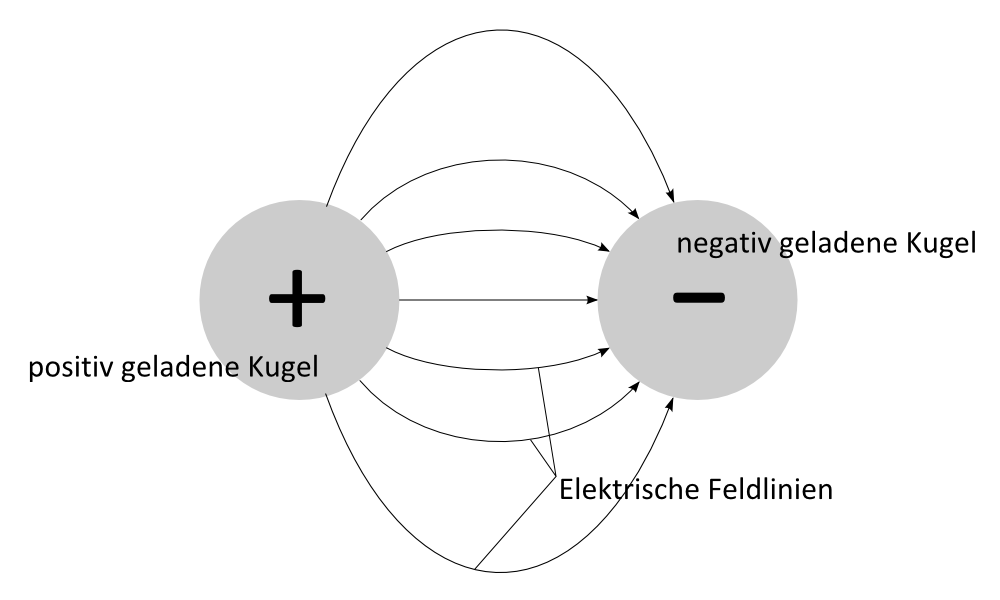
Das elektrische Feld stellt man sich modellhaft so vor, dass Feldlinien zwischen den Ladungen existieren, die immer von der positiven Ladung zur negativen
Ladung gerichtet sind. Das elektrische Feld, bzw. die mit ihm verbundene elektrische Feldstärke ist also eine vektorielle Größe.
Weiterhin gilt, dass die Feldlinien im Gleichgewicht senkrecht auf den jeweiligen Oberflächen stehen.
Das elektrische Feld zwischen Kugelladungen nennt man auch Radialfeld.
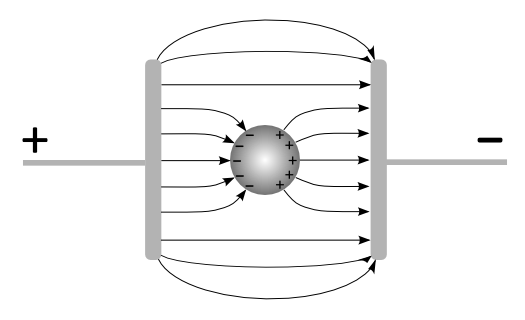
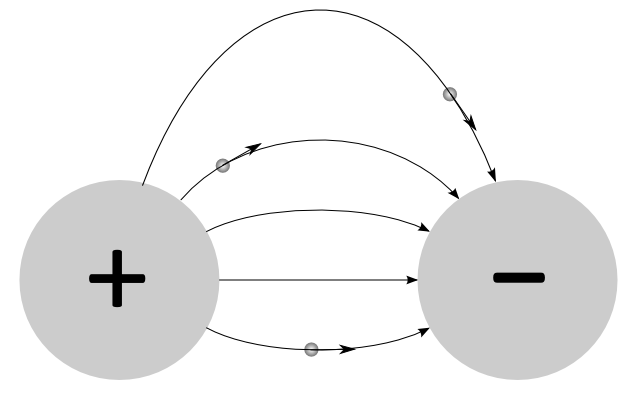 Werden Probeladungen (das sind bewegliche Körperchen, im Gegensatz zu den felderzeugenden unbeweglichen Körpern) in ein elektrisches Feld gebracht,
übt dieses Kräfte auf die Probeladungen aus. Die Richtung der wirkenden Kraft ist jeweils tangential zu den Feldlinien. In der Abbildung sind drei Probeladungen
mit den auf sie wirkenden Kräften gezeigt. Aufgrund der Richtung der Kraft folgt, dass es sich um positive Ladungen handeln muss. Sie werden in Richtung
der Kugel mit der negativen Ladung beschleunigt.
Werden Probeladungen (das sind bewegliche Körperchen, im Gegensatz zu den felderzeugenden unbeweglichen Körpern) in ein elektrisches Feld gebracht,
übt dieses Kräfte auf die Probeladungen aus. Die Richtung der wirkenden Kraft ist jeweils tangential zu den Feldlinien. In der Abbildung sind drei Probeladungen
mit den auf sie wirkenden Kräften gezeigt. Aufgrund der Richtung der Kraft folgt, dass es sich um positive Ladungen handeln muss. Sie werden in Richtung
der Kugel mit der negativen Ladung beschleunigt.
Die elektrischen Feldlinien symbolisieren also die Wirkungsrichtung der Kraft auf eine positive Ladung.
Qualitativ ist auch die Stärke des elektrischen Feldes größer, wenn die Feldlinien dichter zusammen sind. Daraus folgt, dass das elektrische Radialfeld keine konstante Stärke aufweist, da die Feldlinien in unterschiedlichen Abständen von der Kugel auch unterschiedlich dicht verlaufen.
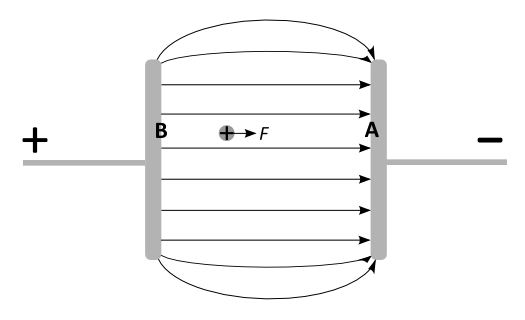
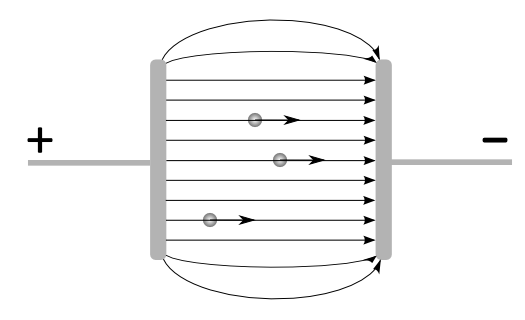 Im Gegensatz dazu bildet das elektrische Feld, dass sich zwischen zwei unterschiedlich geladenen ebenen Metallplatten befindet, eine homogene Feldstärke aus.
Das Feld zwischen den Platten eines Plattenkondensators ist ein homogenes Feld.
Im Gegensatz dazu bildet das elektrische Feld, dass sich zwischen zwei unterschiedlich geladenen ebenen Metallplatten befindet, eine homogene Feldstärke aus.
Das Feld zwischen den Platten eines Plattenkondensators ist ein homogenes Feld.
Streng genommen existiert dieses homogene Feld nur weit entfernt von den Kondensatorplattenrändern. In der Skizze ist angedeutet, dass die Feldlinien an
den Plattenrändern
ähnlich wie beim Radialfeld verlaufen. Im Allgemeinen lässt sich aber die Form der Feldlinien dort nicht bestimmen und wird vernachlässigt.
In der Mitte des Kondensators verlaufen die Feldlinien aber parallel und mit konstantem Abstand zueinander. Die Feldstärke ist also konstant und die Kraft
auf bewegliche Probeladungen ist auch konstant.
Ladungen werden getrennt und bilden zwischen sich ein elektrisches Feld aus. Ladungen können aber auch so weit voneinander getrennt werden, dass man sie
als einzelne Ladung betrachten kann. Auch diese nun vereinzelten Ladungen haben ein elektrisches Feld. Die Form und Richtung der Feldlinien ist die
gleiche wie bei Ladungspärchen; es fehlt aber die zweite Ladung...


Von einer positiven Ladung führen die Feldlinien radialsymmetrisch nach außen, bei einer negativen Ladung zeigen die Feldlinien von außen kommend
senkrecht auf die Ladung.
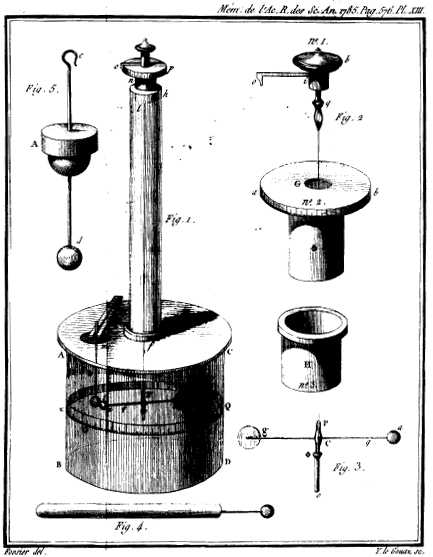 1785 entdeckte Charles Augustin de Coulomb die Gesetzmäßigkeit der Kraftwirkung zwischen geladenen Körpern. Er führte umfangreiche Kraftmessungen
durch, z.B. mit dem abgebildeten Torsionspendel, und formulierte das nach ihm benannte Coulomb'sche Gesetz:
$$
F_C = \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q_1 \cdot Q_2}{r^2}
$$
Es sind $Q_1$ und $Q_2$ zwei Punktladungen und $r$ der Abstand zwischen diesen. $\epsilon_0$ ist die elektrische Feldkonstante mit
$\epsilon_0 = 8,854 \cdot 10^{-12} \frac{\text{As}}{\text{Vm}}$.
1785 entdeckte Charles Augustin de Coulomb die Gesetzmäßigkeit der Kraftwirkung zwischen geladenen Körpern. Er führte umfangreiche Kraftmessungen
durch, z.B. mit dem abgebildeten Torsionspendel, und formulierte das nach ihm benannte Coulomb'sche Gesetz:
$$
F_C = \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q_1 \cdot Q_2}{r^2}
$$
Es sind $Q_1$ und $Q_2$ zwei Punktladungen und $r$ der Abstand zwischen diesen. $\epsilon_0$ ist die elektrische Feldkonstante mit
$\epsilon_0 = 8,854 \cdot 10^{-12} \frac{\text{As}}{\text{Vm}}$.

Die Kraftwirkung ist positiv, wenn sich zwei gleichnamige Ladungen abstoßen, und negativ, wenn sich ungleichnamige Ladungen anziehen.
Für die Kraftwirkung ist es unerheblich, ob die Ladungen tatsächlich als Punktladungen oder verteilt auf einer Kugeloberfläche vorliegen. Der Kraftbetrag bezieht sich immer auf eine Punktladung in der Mitte des Körpers (vgl. hierzu das Prinzip des Massepunktes in der Mechanik).
Elektrische Felder üben Kräfte auf Ladungen bzw. auf geladene Körper aus. Was passiert aber, wenn neutrale Körper in ein elektrisches Feld gebracht werden?
 In neutralen, aber leitfähigen Körpern, z.B. Metallen, existiert eine große Anzahl an freien Ladungsträgern. Wird ein solcher Körper in ein elektrisches
Feld, z.B. in einem Plattenkondensator, gebracht, spüren die freien Ladungsträger dieses Feld und bewegen sich entsprechend der Feldkräfte in Richtung
einer Seite des Kondensators. Durch die Bewegung der Ladungsträger kommt es also zu einer Ladungstrennung innerhalb des neutralen Körpers.
Es entstehen sogenannte Influenzladungen an der Oberfläche des Probekörpers, die sich natürlich wieder auf den Verlauf der Feldlinien auswirken.
Die Feldlinien stoßen senkrecht auf die Influenzladungen. Im Inneren des Probekörpers hingegen ist das elektrische Feld verschwunden. Die Ladungen
des Probekörpers haben sich so lange bewegt, und sind damit den Feldkräften gefolgt, bis sie keinen Kräften mehr ausgesetzt sind. Wenn die Ladungen
aber keine Kräfte mehr erfahren, kann kein elektrisches Feld mehr vorliegen.
In neutralen, aber leitfähigen Körpern, z.B. Metallen, existiert eine große Anzahl an freien Ladungsträgern. Wird ein solcher Körper in ein elektrisches
Feld, z.B. in einem Plattenkondensator, gebracht, spüren die freien Ladungsträger dieses Feld und bewegen sich entsprechend der Feldkräfte in Richtung
einer Seite des Kondensators. Durch die Bewegung der Ladungsträger kommt es also zu einer Ladungstrennung innerhalb des neutralen Körpers.
Es entstehen sogenannte Influenzladungen an der Oberfläche des Probekörpers, die sich natürlich wieder auf den Verlauf der Feldlinien auswirken.
Die Feldlinien stoßen senkrecht auf die Influenzladungen. Im Inneren des Probekörpers hingegen ist das elektrische Feld verschwunden. Die Ladungen
des Probekörpers haben sich so lange bewegt, und sind damit den Feldkräften gefolgt, bis sie keinen Kräften mehr ausgesetzt sind. Wenn die Ladungen
aber keine Kräfte mehr erfahren, kann kein elektrisches Feld mehr vorliegen.
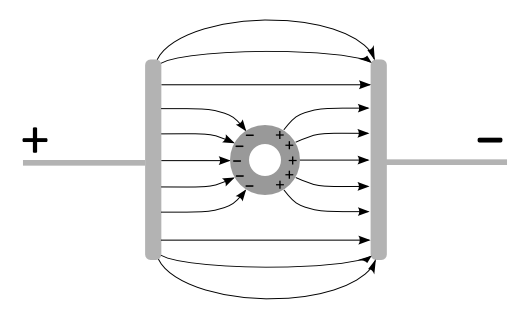 Bei einem Ring aus leitendem Material bleibt das Innere feldfrei (der Faraday'sche Käfig basiert auf
diesem Prinzip). Die Influenzladungen bilden im Körper einen Stromkreis,
wenn das Feld des Kondensators weggenommen wird. Die Ladungen werden durch den Ring fließen und sich
neutralisieren. Das heißt, das elektrische Feld zwischen den Influenenzladungen existiert nur im
Leiterinneren, also ähnlich wie beim Stromkreis, wo der Plus- und der Minuspol durch einen Leiter
miteinander verbunden sind. Der Strom (= bewegte Ladungen) fließt durch den Leiter.
Elektrische Felder gibt es also in Luft und in Festkörpern.
Bei einem Ring aus leitendem Material bleibt das Innere feldfrei (der Faraday'sche Käfig basiert auf
diesem Prinzip). Die Influenzladungen bilden im Körper einen Stromkreis,
wenn das Feld des Kondensators weggenommen wird. Die Ladungen werden durch den Ring fließen und sich
neutralisieren. Das heißt, das elektrische Feld zwischen den Influenenzladungen existiert nur im
Leiterinneren, also ähnlich wie beim Stromkreis, wo der Plus- und der Minuspol durch einen Leiter
miteinander verbunden sind. Der Strom (= bewegte Ladungen) fließt durch den Leiter.
Elektrische Felder gibt es also in Luft und in Festkörpern.
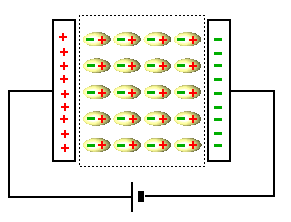 Sind die neutralen Körper nicht leitfähig, tritt ein anderes Phänomen auf, die Polarisation. Die Elektronen in den Atomen sind gebunden, d.h. sie können sich nicht
frei durch den Körper bewegen. Innerhalb des Atoms jedoch können sie der Kraft des äußeren Feldes folgen. Durch die Ladungsverschiebung bilden sich Dipole. So wird der Körper
insgesamt auf der positiven Kondensator-Seite negativ und auf der negativen Kondensator-Seite positiv geladen sein.
Sind die neutralen Körper nicht leitfähig, tritt ein anderes Phänomen auf, die Polarisation. Die Elektronen in den Atomen sind gebunden, d.h. sie können sich nicht
frei durch den Körper bewegen. Innerhalb des Atoms jedoch können sie der Kraft des äußeren Feldes folgen. Durch die Ladungsverschiebung bilden sich Dipole. So wird der Körper
insgesamt auf der positiven Kondensator-Seite negativ und auf der negativen Kondensator-Seite positiv geladen sein.
Wie die Influenz ist auch die Polarisation darauf beschränkt, dass ein elektrisches Feld von außen wirkt. Ohne äußeres Feld gleichen
sich die Ladungen wieder aus und die Effekte verschwinden.
In einem elektrischen Feld wirken Kräfte auf Ladungen. Der Betrag der Kraft hängt dabei von der Größe der Probeladung ab. Eine größere Probeladung erfährt auch eine größere Kraft im Feld. Eine von der Probeladung unabhängige Größe stellt die elektrische Feldstärke dar. Sie ist ein Maß dafür, welche Kraft auf eine Elementarladung im elektrischen Feld wirkt. Dies gilt allgemein und ist nicht auf das homogene Feld beschränkt. Für die Feldstärke hat man das Formelzeichen $\vec{E}$ und es gilt: $$ \text{elektrische Feldstärke} \; \vec{E} \\ \vec{E}= \frac{\vec{F}}{q} \\ \\ \left[\vec{E}\right] = 1 \; \frac{\text{N}}{\text{C}} $$
Damit kann man für die Kraft, die auf eine Probeladung im elektrischen Feld wirkt, aufschreiben: $$ \vec{F} = q \cdot \vec{E} $$ Zur Richtung: Die Richtung des elektrischen Feldes ist gleich der Richtung der wirkenden Kraft auf eine positive Probeladung.
Analog zu der Kraft auf eine Ladung, die durch die elektrische Feldstärke übertragen wird, kann man die Gewichtskraft einer Masse im
Schwerefeld der Erde betrachten. Eine Masse $m$ wird durch die Gravitationskraft in Richtung Erdmittelpunkt beschleunigt. Die
Beschleunigung beträgt in Mitteleuropa etwa $9,81 \frac{\text{m}}{\text{s}^2}$. Dadurch wirkt auf die Masse $m$ die Kraft $F_G = m \cdot g$.
Eine Ladung $q$ wird durch das elektrische Feld $\vec{E}$ beschleunigt und erfährt dabei die Kraft $\vec{F}$.
Im Gegensatz zur Gravitation, die nur eine anziehende Kraft kennt, gibt es im Bereich des elektrischen Feldes eine anziehende und eine
abstoßende Kraft.
Wenn Ladungen getrennt werden, entsteht zwischen ihnen ein elektrisches Feld. Die wirkenden Feldkräfte würden normalerweise dafür sorgen,
dass sich die Ladungen wieder aufeinander zu bewegen und neutralisieren. Um die Ladungen zu trennen, muss also Energie aufgewendet werden.
Andererseits kann man Energie gewinnen, wenn die Ladungen sich gezielt neutralisieren können.
Damit lässt sich sagen, dass der Zustand getrennter Ladungen gespeicherte Energie ist, die bei Bedarf abgerufen werden kann. Die Energiemenge
bezogen auf eine Elementarladung nennt man Spannung und es gilt:
$$
\text{Spannung} \; U \\
U = \frac{W}{q} \\
\left[U\right] = 1 \; \frac{\text{J}}{\text{C}} = 1 \text{V}
$$
Welche Energie ist notwendig, um eine Elektron von der positiven Kondensatorplatte zur negativen Platte zu verschieben?
Allgemein gilt, dass Energie Kraft mal Weg ist. Also:
$$
W = F \cdot d
$$
$d$ ist hier der Abstand zwischen den Kondensatorplatten, der überwunden werden muss. Weiterhin ist bekannt, dass die Kraft auf eine Ladung $q$ durch
den Ausdruck
$$
F = q \cdot E
$$
gegeben ist. Insgesamt folgt daher:
$$
W = q \cdot E \cdot d
$$
Und wegen $W = q \cdot U$ erhält man für die Spannung
$$
U = E \cdot d
$$
Umgeformt:
$$
E = \frac{U}{d}
$$
Damit hat die elektrische Feldstärke eine weitere Einheit:
$$
\left[E\right] = 1 \; \frac{\text{V}}{\text{m}}
$$
In dem Abschnitt wurde übergangen, dass es sich bei $F$, $E$ und $d$ um vektorielle Größen handelt. Da es hier um das elektrische Feld eines Plattenkondensators geht, ist die Richtung des elektrischen Feldes und damit die Wirkungsrichtung der Kraft, sowie auch die Verschiebungsrichtung für ein Elektron klar: Es ist eine geradlinige Bewegung entlang einer Achse, die senkrecht auf den Kondensatorplatten steht.
Die Spannung, die wir berechnen können, ist die Energie, die eine Ladung bei der Bewegung von einem Punkt A zu einem anderen Punkt B benötigt. Wir bewegen die Ladung also zwischen zwei Punkten. Wenn wir nun den einen Punkt, z.B. A, als Bezugspunkt definieren, können wir sagen, dass die Spannung zwischen den beiden Punkten das Potential des Punktes B gegen ein Nullpotential des Bezugspunktes A ist.
Das Potential wird mit dem griechischen Buchstaben $\phi$ (phi) bezeichnet. Das Nullpotential von Bezugspunkt A wäre dann $\phi_A = 0 \; \text{V}$.
Allgemein ist die Spannung zwischen den Punkten A und B die Potentialdifferenz $\phi_B - \phi_A$.
Es gilt:
\begin{align}
U &= \Delta \phi \\
U&= \phi_B - \phi_A
\end{align}
Letzten Endes benötigt man bei der Bestimmung eines Potentials immer einen Bezugspunkt. Ähnlich ist das bei der Bestimmung der mechanischen potentiellen Energie. Hier ist bekanntlich die Höhe des Körpers über einer Bezugsebene entscheidend.
Die potentielle Energie und auch das elektrische Potential ist
also abhängig von der Wahl der Bezugsebene bzw. des Bezugspunktes. In dem Beispiel oben ist die Wahl von $\phi_A = 0$ natürlich sinnvoll, da das positiv
geladene Teilchen an der negativen Kondensatorplatte in seiner Bewegung enden würde. Damit könnte man sagen, dass das Potential die Möglichkeit bietet,
dass sich geladene Teilchen bewegen können.
Oft wird das Nullpotential in einem unendlichen Abstand von der Ladung festgelegt. Eine Probeladung in unendlichem Abstand erfährt somit keine Kräfte
durch das Feld der ortsfesten Ladung.
Analog ist die Anziehungskraft durch die Gravitation in einem unendlichen Abstand ebenfalls Null. Bei beiden Phänomenen nimmt die Kraft mit dem Quadrat des Abstands ab: $F \sim \frac{1}{r^2}$
Ein Radialfeld entsteht, wenn eine punkt- oder kugelförmige Ladung existiert. Wird innerhalb des Radialfeldes eine Probeladung von einem Punkt
A nach einem Punkt B bewegt, so wird entweder Energie frei (Ladung bewegt sich entsprechend der Feldkräfte) oder es muss Energie aufgewendet
werden (Ladung wird gegen die Feldkräfte bewegt).
Im homogenen Feld ist das relativ einfach, da Energie gleich Kraft mal Weg ist und die Kraft auf eine Probeladung konstant ist. Kennt man den
Abstand der Punkte voneinander, kann die Energie, bzw. die notwendige Arbeit berechnet werden.
In einem Radialfeld hingegen ist die Kraft auf eine Probeladung abhängig von dem Abstand zur Feldladung, d.h. es gilt $F = F(r)$.
 Wird z.B. eine negative Probeladung in einem Radialfeld einer negativen Feldladung von einem Punkt $A$ zu einem Punkt $B$ bewegt, muss Energie
aufgewendet werden, denn die Probeladung muss sich gegen die Feldkräfte bewegen.
Wird z.B. eine negative Probeladung in einem Radialfeld einer negativen Feldladung von einem Punkt $A$ zu einem Punkt $B$ bewegt, muss Energie
aufgewendet werden, denn die Probeladung muss sich gegen die Feldkräfte bewegen.
Die Feldkräfte hängen widerum von dem Abstand der Probeladung zur Feldladung, genauer zum Mittelpunkt der Feldladung ab. Die Abstände sind
in dem Beispiel $r_A$ und $r_B$. Mit dem Coulomb-Gesetz kann man nun für jeden Abstand $r$ die Kraft bestimmen, die auf die Probeladung wirkt,
und in einem $r-F-$Diagramm auftragen.
Beträgt die Feldladung z.B. $Q_1 = - 10 \text{ μC}$ und die Probeladung $q_2 = - 5 \text{ μC}$ erhält man die folgende Wertetabelle und das
dazugehörige Diagramm:
| $r$ in mm | $F$ in N |
|---|---|
| 1 | 449590 |
| 2 | 112398 |
| 3 | 49954 |
| 4 | 28099 |
| 5 | 17984 |
| 10 | 4496 |
| 20 | 1124 |
| 30 | 500 |
| 40 | 281 |
| 50 | 180 |
| 1000 | 0,45 |
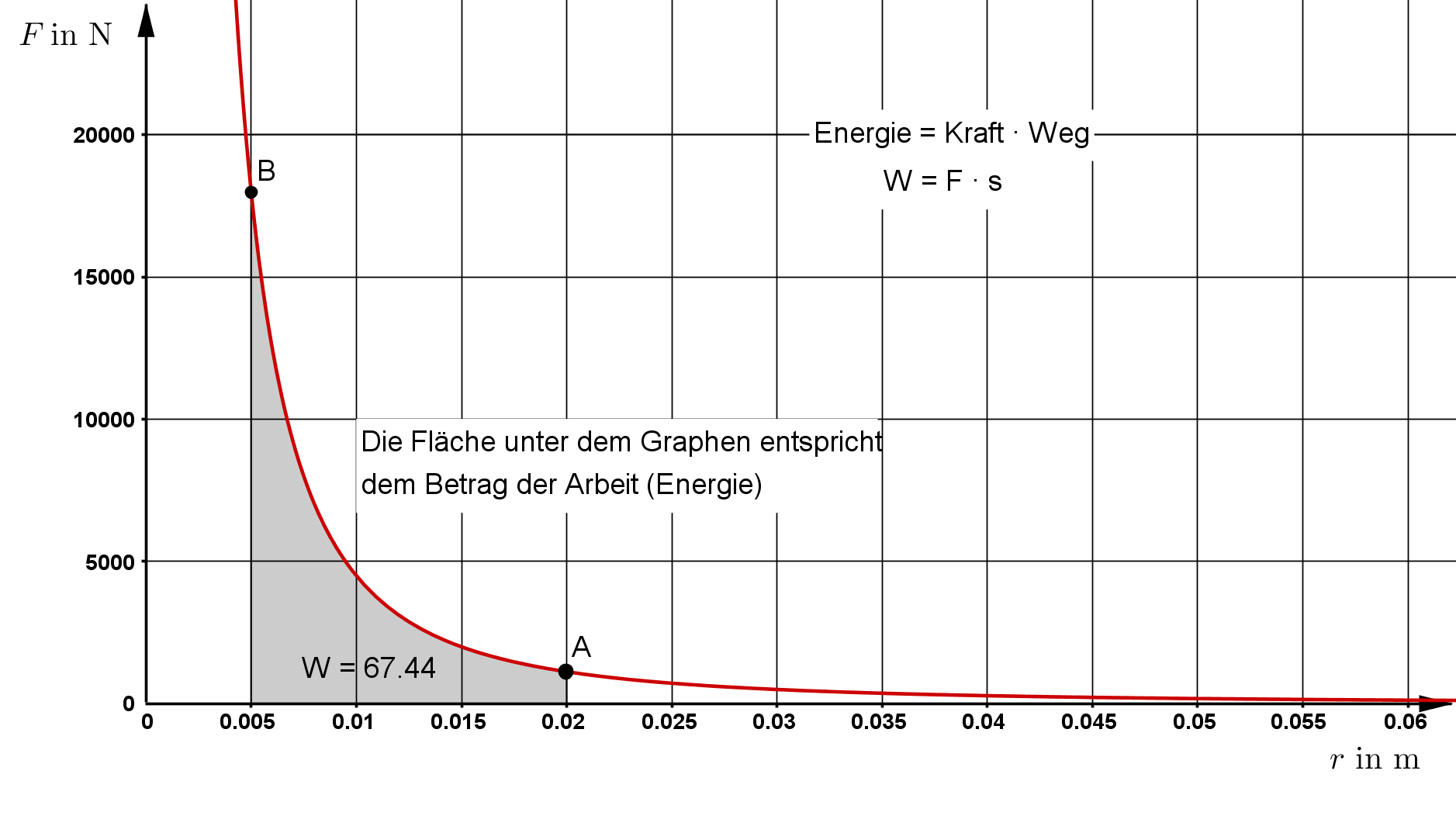
In dem Beispiel wird die Probeladung von einer Entfernung von $r_A = 20 \text{ mm}$ auf eine
Entfernung von $r_B = 5 \text{ mm}$ gebracht. Die dafür notwendige Energie entspricht der Fläche unter dem
Graphen im $r-F-$Diagramm.
Bestimmt werden kann diese Fläche durch das Integral der Funktion $F(r)$ von $r_A$ nach $r_B$.
\begin{align}
W &= \int_{r_A}^{r_B} F(r) dr \\ \\
W &= \int_{r_A}^{r_B} \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q_1 \cdot q_2}{r^2} dr \\ \\
W &= \frac{Q_1 \cdot q_2}{4 \pi \epsilon_0} \int_{r_A}^{r_B} \frac{1}{r^2} dr \\ \\
W &= \frac{Q_1 \cdot q_2}{4 \pi \epsilon_0} \cdot \left[ - \frac{1}{r_B} + \frac{1}{r_A} \right] \\ \\
W &= \frac{Q_1 \cdot q_2}{4 \pi \epsilon_0} \cdot \left[ \frac{1}{r_A} - \frac{1}{r_B} \right] \\ \\
W &= \frac{- 10 \cdot 10^{-6} \text{ C} \cdot \left(- 5 \cdot 10^{-6} \text{ C} \right)}{4 \pi \cdot 8,85 \cdot 10^{-12} \, \frac{\text{As}}{\text{Vm}}} \cdot \left[ \frac{1}{0,02 \text{ m}} - \frac{1}{0,005 \text{ m}} \right] \\ \\
W &= - 67,44 \text{ J}
\end{align}
Das negative Vorzeichen besagt, dass Energie hineingesteckt werden muss, um diese Annäherung zu erreichen. Würde man z.B. eine positive Probeladung in das Radialfeld bringen und die gleiche Entfernungsänderung durchführen, wäre eine Ladung in der Formel positiv und eine negativ, insgesamt also negativ. Zusammen mit der Annäherung ergibt sich somit ein positiver Betrag für die Arbeit. Es würde Energie frei.
Wird eine Probeladung in einem Radialfeld von $A$ nach $B$ bewegt, erfolgt eine Energieänderung in dem System nach: $$ W = \frac{Q_1 \cdot q_2}{4 \pi \epsilon_0} \cdot \left[ \frac{1}{r_A} - \frac{1}{r_B} \right] $$ Dabei ist es unwichtig, auf welchem Weg die Probeladung verschoben wird. Wichtig sind nur die Abstände vor und nach der Bewegung.
Bezieht man die Energieänderung nun auf die Probeladung, ergibt sich der folgende Ausdruck:
$$
\frac{W}{q_2} = \frac{Q_1}{4 \pi \epsilon_0} \cdot \left[ \frac{1}{r_A} - \frac{1}{r_B} \right]
$$
Das ist ein Ausdruck, der die Spannung zwischen zwei Punkten im Radialfeld angibt. Also gilt für die Spannung
zwischen den Punkte $A$ und $B$ im Radialfeld der Ladung $Q$:
$$
U = \frac{Q}{4 \pi \epsilon_0} \cdot \left[ \frac{1}{r_A} - \frac{1}{r_B} \right]
$$
In der Gleichung steckt aber eine Differenz drin, nämlich
$$
U = \frac{Q}{4 \pi \epsilon_0} \cdot \frac{1}{r_A} - \frac{Q}{4 \pi \epsilon_0} \cdot \frac{1}{r_B}
$$
Da die Spannung auch die Differenz zweier Potentiale darstellt ($U = \phi_A - \phi_B$), hat man nun einen Ausdruck für das Potential
eines Punktes $A$ im Radialfeld der Ladung $Q$:
$$
\phi_A = \frac{Q}{4 \pi \epsilon_0} \cdot \frac{1}{r_A}
$$
$r_A$ ist dabei der Abstand des Punktes $A$ vom Mittelpunkt der Feldladung $Q$.
Für die Energie eines elektrischen Feldes gilt allgemein:
Die Energie eines Systems sinkt, wenn dessen Feldkräfte Ladungen verschieben. Wenn von äußeren Kräften Ladungen gegen die Feldkräfte verschoben werden, steigt die Energie.Soll ein Elektron von der positiven Seite eines Plattenkondensators auf die negative Seite verschoben werden, wird Energie benötigt. Dies lässt sich mit $W = q \cdot U$ berechnen. Durch die zusätzliche Ladung auf der negativen Seite wird aber die Spannung zwischen den beiden Seiten vergrößert. Für das nächste Elektron wird also etwas mehr Energie benötigt, um es auf die negative Seite zu verschieben. Die dann insgesamt zur Verfügung stehende Energie aufgrund der Ladungstrennung ist also größer geworden.
Zu Beginn der Elektronenverschiebung, also wenn die Kondensatorplatten noch ungeladen sind, ist die anliegende Spannung Null. Wenn das letzte Elektron verschoben wird, ist die Spannung maximal. Da der Zusammenhang zwischen Ladungsmenge und Spannung proportional ist, ist eine mittlere Spannung für die Verschiebungsenergie pro Elektron anzunehmen. Es folgt $\bar U = \frac12 U_{max}$ für die mittlere Spannung. Aufsummiert über alle Elektronen folgt für die im elektrischen Feld gespeicherte Energiemenge (Feldenergie oder Systemenergie): $$ W = \frac12 \cdot Q \cdot U $$
© mondbrand MMXIX