

Eine Potenzfunktion liegt dann vor, wenn die Variable $x$ als Basis mit einer Zahl $n$ als Exponent potenziert wird. Es folgt also als Funktionsgleichung: $$ f(x) = x^n $$ Zunächst bezeichnet $n$ eine beliebige Zahl aus dem Bereich der natürlichen Zahlen (inklusive Null).
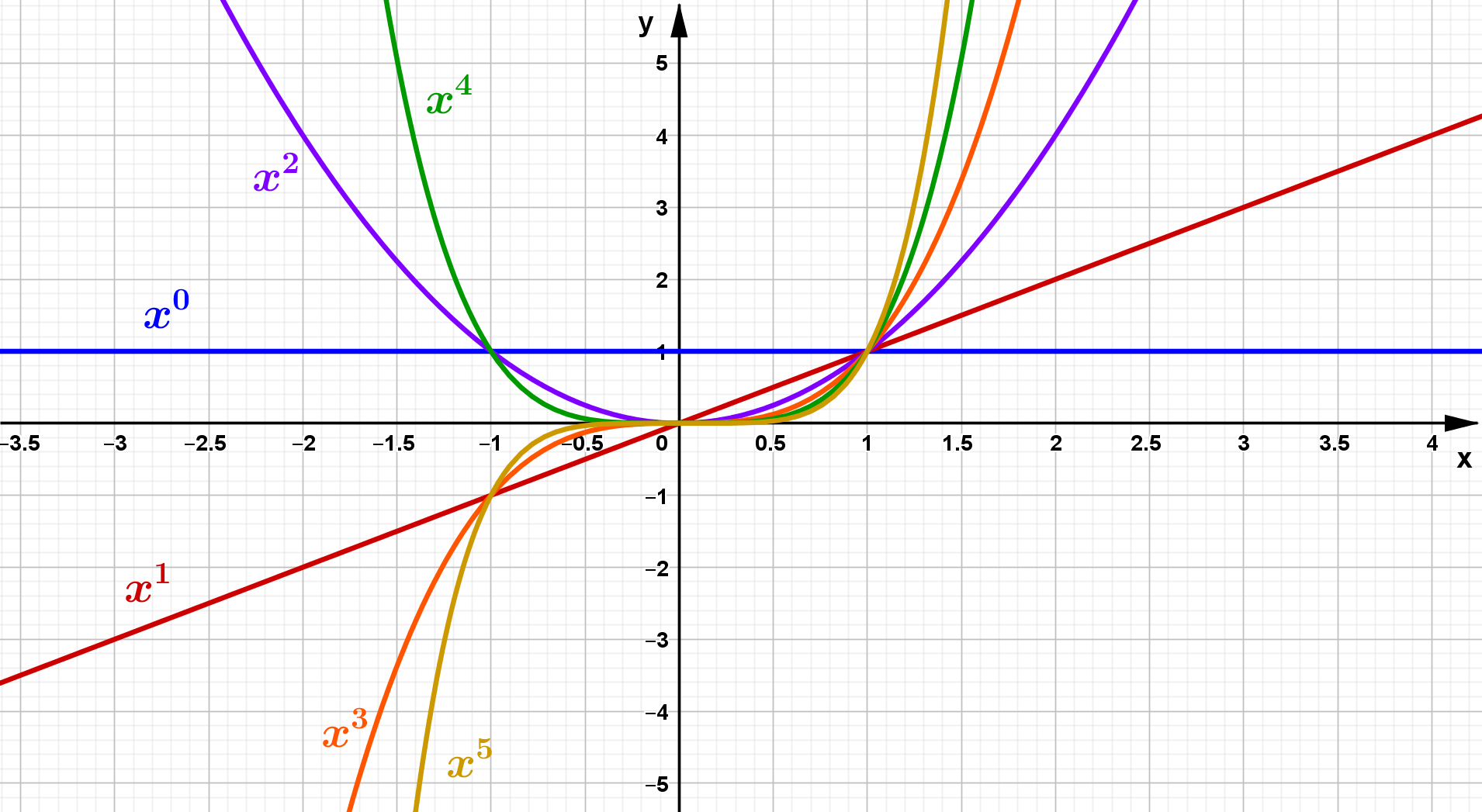
Für geradzahlige Exponenten verlaufen die Graphen ausschließlich im ersten und zweiten Quadranten. Sind die Exponenten ungerade, verlaufen die
Graphen im ersten und dritten Quadranten.
Für alle Funktionen gilt, dass der Punkt $P (1/1)$ Bestandteil des Graphen ist.
Ein weiterer gemeinsamer Punkt ist $Q (-1/1)$ für Funktionen mit geradzahligem Exponenten,
bzw. $R (-1/-1)$ für Funktionen mit ungeradzahligem Exponenten.
Die Graphen sind für größer werdende Exponenten immer mehr gestreckt und nähern sich einer Kastenform an.
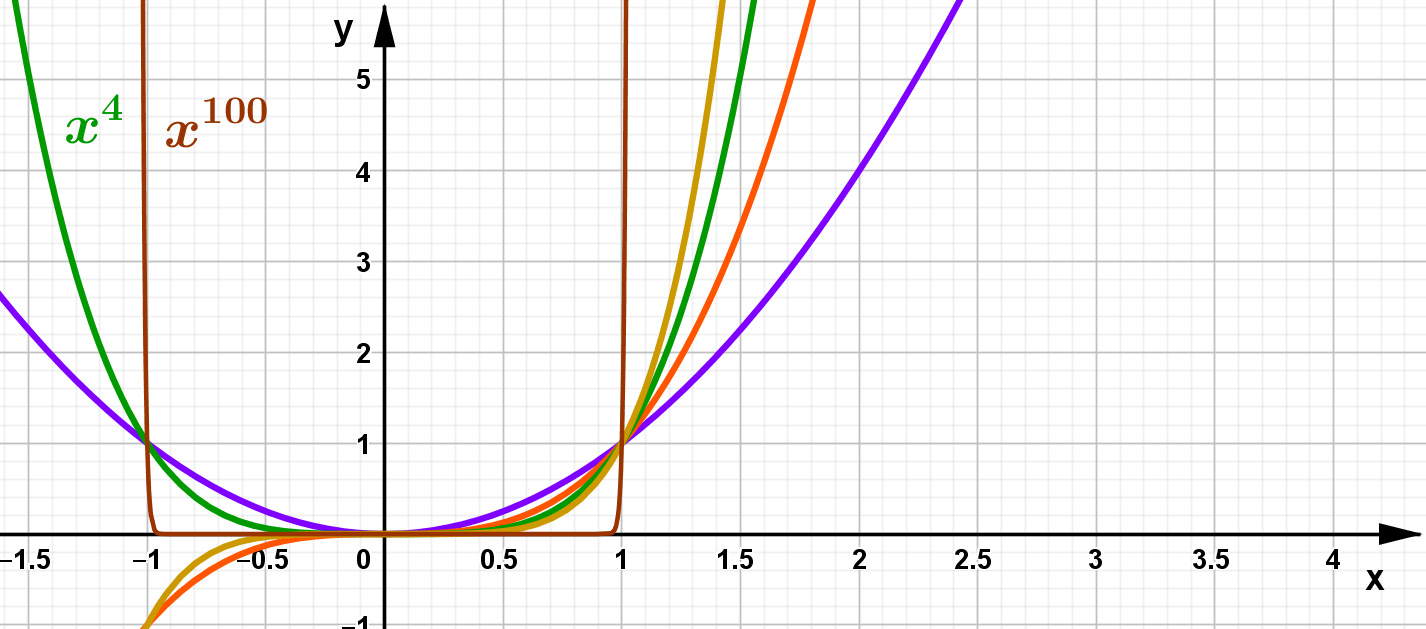
Eine weitere typische Eigenschaft ist, dass bei allen Funktionen der Funktionswert für größer werdende $x$-Werte immer größer wird. Im Extremfall
gilt: $f(x \rightarrow \infty) \rightarrow \infty$
Für Funktionen mit geradzahligem Exponenten gilt weiterhin, dass für kleiner werdende $x$-Werte der Funktionswert größer wird. Auch hier gilt im
Extremfall: $f(x \rightarrow - \infty) \rightarrow \infty$
Bei den Funktionen mit ungeradzahligem Exponenten gilt im Extremfall: $f(x \rightarrow - \infty) \rightarrow - \infty$
Eine Übersicht über das Globalverhalten gibt es hier.
Die Symmetrie des Graphen bildet noch eine wesentliche Eigenschaft der Potenzfunktionen. Wenn der Exponent des Funktionsterms geradzahlig ist,
dann ist der Funktionsgraph symmetrisch bezüglich der $y$-Achse (Achsensymmetrie).
Ist hingegen der Exponent ungeradzahlig, ist der Graph symmetrisch bezüglich des Koordinatenursprungs (Punktsymmetrie).
Eine Übersicht über das Symmetrieverhalten gibt es hier.
In den allermeisten Fällen kann ein funktioneller Zusammenhang nicht ausschließlich mit Hilfe einer Potenz gebildet werden. Meistens werden mehrere Potenzfunktionen benötigt, die alle mit ihren typischen Eigenschaften dafür sorgen, dass der dazugehörige Graph einen bestimmten Verlauf besitzt. Die Eigenschaften solcher Funktionen, die aus der Summe mehrerer Potenzfunktionen bestehen, werden im Kapitel Ganzrationale Funktionen behandelt.
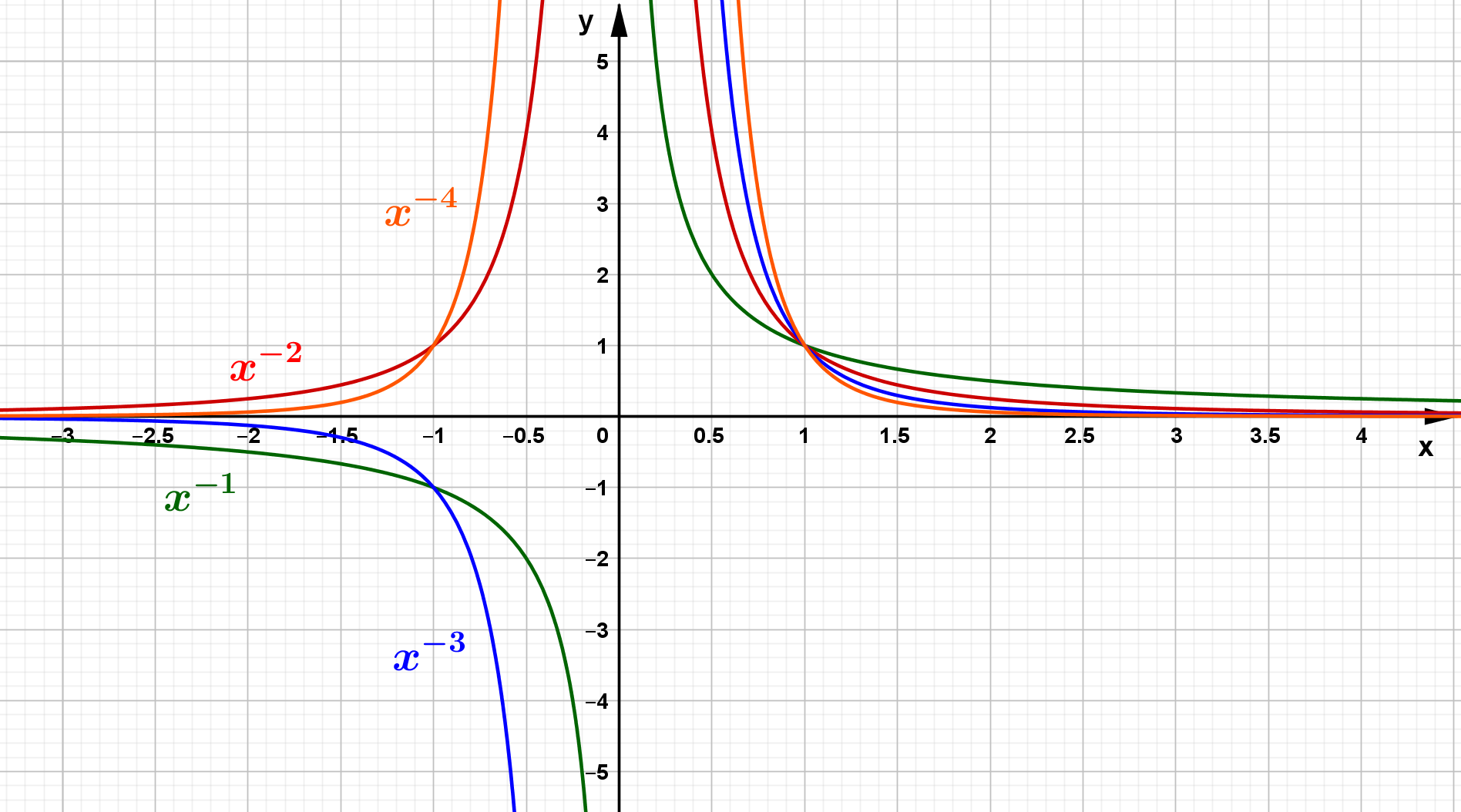
Potenzfunktionen mit negativem Exponenten besitzen etwas andere Eigenschaften. Es gilt aber auch für diese Funktionen, dass komplexere Sachzusammenhänge (meistens) nicht ausschließlich durch Potenzfunktionen dargestellt werden können. Hier werden die Eigenschaften im Kapitel gebrochen-rationale Funktionen behandelt.
© mondbrand MMXIX